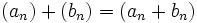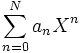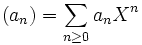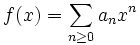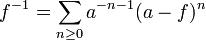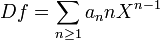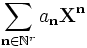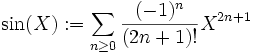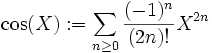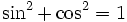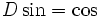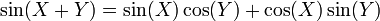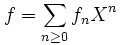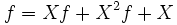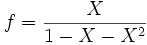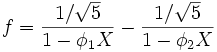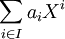- Serie formelle
-
Série formelle
En mathématiques, les séries formelles sont un outil qui permet d'utiliser l'arsenal analytique des séries entières sans tenir compte de la notion de convergence. Pour cela on construit une série, non pas comme une fonction à l'aide d'une variable x, mais comme un être algébrique à l'aide d'une indéterminée X. Ces séries sont également très utiles pour décrire de façon concise des suites et pour trouver des formules pour des suites définies par récurrence via ce que l'on appelle les fonctions génératrices.
Considérons un anneau commutatif R. Nous voudrions définir l'anneau des séries formelles sur R de l'indéterminée X, noté R[[X]] ; n'importe quel élément de cet anneau peut être écrit de façon unique comme une somme infinie de la forme ∑n≥0 an Xn où les coefficients an sont des éléments de R. En fait, R[[X]] est un anneau topologique et ces sommes infinies sont définies correctement et convergent, non pas au sens d'une fonction mais au sens des séries formelles. L'addition et la multiplication sont les mêmes que pour les séries entières.
Sommaire
Une construction formelle
Considérons l'ensemble RN de toutes les suites infinies à valeurs dans R et définissons la somme de deux telles suites de la façon suivante :
et leur produit de cette façon :
Le produit est appelé produit de Cauchy de deux suites de coefficients et est une sorte de produit de convolution discret. Ces deux opérations font de RN un anneau commutatif dont l'élément neutre pour la multiplication est (1,0,0,...). Nous identifierons l'élément a de R à la suite (a,0,0,...) et nous définissons X comme étant égal à (0,1,0,0,...). Alors tout élément de RN de la forme (a0, a1, a2,...,aN,0,0,...) peut être écrit comme une somme finie de cette façon :
Afin d'étendre ce développement aux séries infinies, nous avons besoin d'une distance sur RN : définissons d((an), (bn)) = 2-k, où k est le plus petit entier naturel tel que ak ≠ bk (si un tel k n'existe pas, alors les deux suites seront dites égales et la distance de l'une à l'autre est par conséquent nulle). C'est une distance qui fait de RN un anneau topologique, et l'expression
peut maintenant être écrite de façon rigoureuse en utilisant la notion de convergence issue de d ; en fait, tout réarrangement de la série converge vers la même limite.
Cet anneau topologique est l'anneau des séries formelles sur R et se note R[[X]].
Propriétés
R[[X]] est une algèbre associative sur R qui contient l'anneau R[X] des polynômes à coefficients dans R ; les polynômes correspondent aux suites dont le terme vaut 0 à partir d'un certain rang.
La formule de la série géométrique est valable dans R[[X]] :
Un élément ∑ an Xn de R[[X]] est inversible dans R[[X]] si et seulement si son coefficient constant a0 est inversible dans R. Cela implique que le radical de Jacobson de R[[X]] est l'idéal engendré par X et le radical de Jacobson de R.
Les idéaux maximaux de R[[X]] dérivent tous de R de la manière suivante : un idéal M de R[[X]] est maximal si et seulement si M ∩ R est un idéal maximal de R et M est engendré en tant qu'idéal par X et par M ∩ R.
Plusieurs propriétés algébriques de R sont transmises à R[[X]] :
- si R est un anneau local, alors il en est de même pour R[[X]]
- si R est un anneau noethérien, alors il en est de même pour R[[X]]
- si R est intègre, alors il en est de même pour R[[X]]
- si R est un corps, alors R[[X]] est un anneau à valuation discrète.
L'espace métrique (R[[X]], d) est complet. La topologie sur R[[X]] est la topologie produit sur RN où R est muni de la topologie discrète. Par conséquent, d'après le théorème de Tychonov, l'espace R[[X]] est compact si et seulement si R est fini. La topologie sur R[[X]] peut également être vue comme la topologie I-adique, où I = (X) est l'idéal engendré par X (il s'agit de l'idéal formé des séries formelles dont le coefficient d'indice 0 est nul).
Si K=R est un corps, il est possible de considérer le corps des fractions de l'anneau intègre K[[X]] ; il est noté K((X)). Ses éléments sont les séries formelles de Laurent, de la forme :
où M est un entier qui dépend de la série de Laurent f. K((X)) est un corps topologique.
Les séries formelles forment une algèbre de Kleene.
Les séries formelles vues comme des fonctions
En analyse, une série entière convergente définit une fonction à valeurs réelles ou complexes. Les séries formelles peuvent également être vues comme des fonctions dont les ensembles de départ et d'arrivée sont à manier avec précaution. Si f=∑an Xn est un élément de R[[X]], S une algèbre commutative et associative sur R, I un idéal de S tel que la topologie I-adique sur S soit complète, et x un élément de I, alors il est possible de définir :
Cette série converge dans S grâce à l'hypothèse sur x. De plus :
- (f + g)(x) = f(x) + g(x)
et
- (fg)(x) = f(x)g(x)
Toutefois, ces formules ne sont pas des définitions et doivent être démontrées.
Puisque la topologie sur R[[X]] est la topologie (X)-adique et que R[[X]] est complet, il est possible d'appliquer une série formelle à une autre série formelle, à condition que les arguments n'aient pas de coefficient constant: f(0), f(X2-X) et f( (1-X)-1 - 1) sont tous bien définis pour toute série formelle f∈R[[X]].
Avec ce formalisme, nous pouvons donner une formule explicite pour l'inverse (au sens multiplicatif) d'une série formelle f dont le coefficient constant a=f(0) est inversible dans R:
Si la série formelle g avec g(0) = 0 est donnée implicitement par l'équation
- f(g) = X
où f est une série entière connue vérifiant f(0) = 0, alors les coefficients de g peuvent être calculés explicitement en utilisant le théorème d'inversion de Lagrange.
Dérivation de séries formelles
Si f = ∑ an Xn est un élément de R[[X]], on définit sa dérivée formelle en utilisant l'opérateur D défini par
Cette opération est R-linéaire :
- D(af + bg) = aDf + bDg
pour a, b dans R et f, g dans R[[X]].
Beaucoup de propriétés de la dérivation classique des fonctions sont valables pour la dérivation des séries formelles. Par exemple, la règle de dérivation d'un produit est valable :
- D(fg) = f(Dg) + (Df)g
ainsi que la règle de dérivation d'une composée :
- D(f(u)) = (Df)(u)Du
Dans un certain sens, toutes les séries formelles sont des séries de Taylor, car si f=∑an Xn, en écrivant Dk comme la ke dérivée formelle, on trouve que
- (Dkf)(0) = k!ak.
On peut également définir la dérivation pour des séries formelles de Laurent d'une façon naturelle, et dans ce cas, la règle du quotient, en plus des règles énumérées ci-dessus, sera également valable.
Séries formelles de plusieurs variables
La façon la plus rapide de définir l'anneau R[[X1,...,Xr]] des séries formelles sur R en r variables commence avec l'anneau S = R[X1,...,Xr] des polynômes sur R. Soit I l'idéal de S engendré par X1,...,Xr ; considérons alors la topologie I-adique sur S et complétons-la. Le résultat de cette complétion est un anneau topologique complet contenant S et qui est noté R[[X1,...,Xr]].
Pour n=(n1,...,nr)∈Nr, on écrit Xn = X1n1...Xrnr. Alors chaque élément de R[[X1,...,Xr]] de manière unique comme une somme de la façon suivante :
Ces sommes convergent pour n'importe quel choix des coefficients an∈R et l'ordre dans lequel les éléments sont sommés n'a pas d'importance.
Si J est un idéal de R[[X1,...,Xr]] engendré par X1,...,Xr (i.e. J est constitué des séries dont tous les coefficients sont non nuls), alors la topologie sur R[[X1,...,Xr]] est la topologie J-adique.
Puisque R[[X1]] est un anneau commutatif, on peut définir son anneau des séries formelles, noté R[[X1]][[X2]]. Cet anneau est naturellement isomorphe à l'anneau R[[X1,X2]] défini prédemment, mais ces anneaux sont topologiquement différents.
Si K = R est un corps, alors toutes les séries de K[[X1,...,Xr]] sont décomposables en facteurs premiers.
Comme pour les séries formelles à une variable, on peut « appliquer » une série formelle à plusieurs variables à une autre série formelle à condition que son coefficient constant a(0,...,0) soit nul. Il est aussi possible de définir des dérivées partielles de ces séries formelles. Les dérivées partielles commutent comme elles le font pour des fonctions continuement différentiables.
Applications
On peut utiliser des séries formelles pour prouver certaines propriétés en analyse de manière extrêmement simple.
Formules trigonométriques : Considérons les éléments suivants de Q[[X]]:
Alors on peut montrer que
et
aussi bien que
(La dernière expression étant définie sur l'anneau Q[[X,Y]]).
Détermination du terme général d'une suite : Comme exemple de la méthode de la fonction génératrice, considérons le problème consistant à trouver le terme général de la suite de Fibonacci fn définie par f0 = 0, f1 = 1, et fn = fn−1 + fn−2 pour n ≥ 2.
Dans l'anneau R[[X]], on définit la série formelle
f est appelée la fonction génératrice de la suite (fn). La fonction génératrice de la suite (fn−1) est Xf et celle de (fn−2) est X2f. D'après la relation de récurrence sur la suite (fn), nous pouvons écrire que Xf + X2f est identique à f sauf pour les deux premiers coefficients. On obtient alors la relation
(C'est le point le plus important : une relation de récurrence sur une suite se traduit par une équation sur la fonction génératrice associée). Il suffit alors de résoudre l'équation précédente. On obtient :
Le dénominateur peut se factoriser en utilisant le nombre d'or et son conjugué
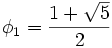 et
et 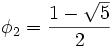
et la décomposition en éléments simples donne
On reconnaît, dans ces deux séries formelles, des séries géométriques. En identifiant leurs coefficients à celui de f, on obtient l'égalité suivante :
Propriété universelle
L'anneau des séries formelles R[[X1, ..., Xr]] possède la propriété suivante :
- Si S est une algèbre commutative et associative sur R
- Si I est un idéal de S tel que S soit complet pour la topologie I-adique
- Si x1, ..., xr sont r éléments de I,
Alors, il existe une unique application Φ : R[[X1, ..., Xr]] -> S vérifiant
- Φ est un homomorphisme d'algèbre
- Φ est continue
- Φ(Xi) = xi pour tout i = 1, ..., r.
Séries formelles généralisées
Soit R un anneau commutatif,
Soit G un groupe commutatif muni d'un ordre total compatible avec l'addition , c’est-à-dire tel que a < b équivaut à a + c < b + c pour tout c de G.
On considère l'ensemble des sous-ensembles I de G bien ordonnés, c'est-à-dire tels que I ne possède pas de chaine infinie décroissante.
On peut alors construire l'ensemble R((G)) des sommes
où ai sont des éléments de R et où on suppose que, pour chaque ensemble d'indexation I, si tous les ai sont nul alors la somme est nulle.
Alors R((G)) est l'anneau des séries formelles sur G, car la condition que l'ensemble d'indexation I soit bien ordonné assure que le produit est bien défini. On suppose évidemment que deux éléments qui diffèrent de zéro sont égaux.
Diverses propriétés de R peuvent se transférer à R((G).
- Si R est un corps, il en est de même de R((G)).
- Si R est un corps ordonné, on peut définir sur R((G)) une relation d'ordre en affectant à chaque série le signe de son coefficient dominant : le coefficient associé au plus petit i tel que ai soit non nul.
- Si G est un groupe divisible et R un corps ordonné tel que R(i) (avec i2 = − 1) soit algébriquement clos alors il en est de même de R((G))
- Enfin, si G est un groupe divisible et R un corps algébriquement clos alors il en est de même de R((G))
Cette théorie a été développée par le mathématicien autrichien Hans Hahn
- Portail des mathématiques
Catégorie : Série
Wikimedia Foundation. 2010.