- Réaction-diffusion
-
Système à réaction-diffusion
Un système à réaction-diffusion est un modèle mathématique qui décrit l'évolution des concentrations d'une ou plusieurs substances spatialement distribuées et soumises à deux processus : un processus de réactions chimiques locales, dans lequel les différentes substances se transforment, et un processus de diffusion qui provoque une répartition de ces substances dans l'espace.
Cette description implique naturellement que de tels systèmes sont appliqués en chimie. Cependant, ils peuvent aussi décrire des phénomènes dynamiques de nature différente : la biologie, la physique, la géologie ou l'écologie sont des exemples de domaines où de tels systèmes apparaissent. Mathématiquement, les systèmes à réaction-diffusion sont représentés par des équations différentielles partielles paraboliques semi-linéaires qui prennent la forme générale de
où chaque composante du vecteur
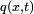 représente la concentration d'une substance,
représente la concentration d'une substance, 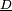 est une matrice diagonale de coefficients de diffusion, Δ désigne le Laplacien et R représente toutes les réactions locales. Les solutions d'une équation de réaction-diffusion peuvent présenter des comportements très divers parmi lesquels la formation d'ondes progressives et de phénomènes ondulatoires ou encore de motifs entropiques (bandes, hexagones et d'autres motifs plus complexes tels que les solitons dissipatifs).
est une matrice diagonale de coefficients de diffusion, Δ désigne le Laplacien et R représente toutes les réactions locales. Les solutions d'une équation de réaction-diffusion peuvent présenter des comportements très divers parmi lesquels la formation d'ondes progressives et de phénomènes ondulatoires ou encore de motifs entropiques (bandes, hexagones et d'autres motifs plus complexes tels que les solitons dissipatifs).Équations de réaction-diffusion à une composante
L'équation de réaction-diffusion la plus simple, ne portant que sur la concentration u d'une seule substance dans une seule dimension de l'espace,
est aussi appelée « équation KPP » (pour Kolmogorov-Petrovsky-Piskounov)[1]. Si le terme en R(u) (qui représente le facteur de réaction chimique dans le processus) vient à s'annuler, l'équation modélise une simple diffusion. L'équation correspondante est alors l'équation de la chaleur. Si R(u) = u(1 − u), on obtient l'équation de Fisher qui était utilisée, à l'origine, pour décrire la propagation de populations d'individus biologiques. L'équation de Newell-Whitehead-Segel est obtenue avec R(u) = u(1 − u2) et décrit le phénomène de convection de Rayleigh-Bénard et, avec R(u) = u(1 − u)(u − α) et 0 < α < 1, on obtient l'équation de Zeldovich, plus générale, qui est employée notamment dans la théorie de la combustion. Notons que le cas R(u) = u2u3 est le cas particulier de dégénération dans l'équation de Zeldovich et que l'équation ainsi obtenue est aussi parfois appelée équation de Zeldovich.
La dynamique des systèmes à une composante est sujette à certaines contraintes dans la mesure où l'équation peut aussi être écrite sous la forme variationnelle
et décrit ainsi une diminution permanente de la "free energy" ⇔ merci d'apporter votre expertise, et de préciser
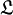 donnée par l'équation fonctionnelle
donnée par l'équation fonctionnelleoù V(u) est un potentiel tel que
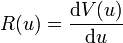 .
.Dans les systèmes à plus d'une solution homogène stationnaire, une solution typique est celle de fronts d'onde assurant la transition entre deux états homogènes. Ces ondes solutions se déplacent à vitesse constante sans changer de géométrie et sont de la forme
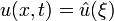 avec ξ = x − ct où c est la célérité de l'onde. Notons qu'alors que les ondes sont, dans un cas standard, des structures stables, toutes les solutions stationnaires non monotones (par exemple, les domaines localisés composés d'un couple front d'onde/contre-front d'onde) sont instables. Pour c = 0, ceci se prouve de manière simple : si u0(x) est une solution stationnaire et si
avec ξ = x − ct où c est la célérité de l'onde. Notons qu'alors que les ondes sont, dans un cas standard, des structures stables, toutes les solutions stationnaires non monotones (par exemple, les domaines localisés composés d'un couple front d'onde/contre-front d'onde) sont instables. Pour c = 0, ceci se prouve de manière simple : si u0(x) est une solution stationnaire et si 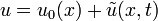 une solution infinitésimalement perturbée, l'analyse de la stabilité linéaire donne l'équation
une solution infinitésimalement perturbée, l'analyse de la stabilité linéaire donne l'équationRéférences
- ↑ A. Kolmogorov et al., Moscow Univ. Bull. Math. A 1 (1937): 1, 1937
- Portail des mathématiques
- Portail de la chimie
Catégorie : Équation aux dérivées partielles
Wikimedia Foundation. 2010.

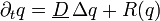
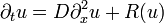
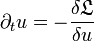
![\mathfrak L=\int\limits_{-\infty}^\infty\left[\frac
D2(\partial_xu)^2+V(u)\right]\text{d}x](/pictures/frwiki/97/a650deebe126ea3b8f08d2e13895304d.png)