- Recurrence transfinie
-
Récurrence transfinie
La récurrence transfinie, appelée aussi sous l'influence anglaise induction transfinie, permet de construire des objets et de démontrer des théorèmes sur des ensembles infinis.Elle généralise la récurrence ordinaire sur N en considérant des familles indexées par un ordinal infini quelconque au lieu de se borner au plus petit qu'est N, appelé ω en tant que nombre ordinal.
Une fois compris ce qu'est un ordinal, on dispose là d'un outil très commode, que l'on peut utiliser conjointement avec l'axiome du choix à la place du lemme de Zorn, pour faire des constructions conformes à l'intuition et où l'on dispose de renseignements précis pour une étude approfondie.
Sommaire
Notions préliminaires
Comme nous parlerons beaucoup des ordinaux dans cet article il peut être pertinent de rappeler que :
Les ordinaux sont des sortes de nombres. C’est-à-dire que le début de la classe des ordinaux (ceux plus petits que ω) peut être identifié à l'ensemble
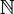 des nombres naturels, et que les relations donnant à
des nombres naturels, et que les relations donnant à 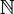 sa structure (successeur, somme, produit ...?) peuvent être étendues à cet ensemble des ordinaux.
sa structure (successeur, somme, produit ...?) peuvent être étendues à cet ensemble des ordinaux.Domaine d'application
La récurrence transfinie s'applique à des ensembles ou des classes munis d'une relation de bon ordre.
- Comme tout ensemble muni d'une relation de bon ordre est isomorphe (pour l'ordre) à un et un seul ordinal (où la relation de bonne ordre est la relation d'appartenance), nous étudierons essentiellement la récurrence infinie sur les seuls ordinaux. Les résultats étant transposables par isomorphisme.
- L'extension de la méthode à tout ensemble est possible via l'utilisation du théorème de Zermelo, équivalent (modulo ZF) à l'axiome du choix, et qui affirme que tout ensemble peut être muni d'une relation de bon ordre. Par exemple il faut l'axiome du choix pour affirmer que R, l'ensemble des réels, est bien ordonnable.
Démonstration par récurrence transfinie
- L'objectif est de démontrer qu'une certaine propriété vaut pour tout objet d'un domaine considéré.
- En arithmétique on dispose d'un schéma d'axiomes permettant de le faire sur l'ensemble des entiers, voir raisonnement par récurrence.
- En théorie des ensembles c'est un théorème applicable à toute classe bien ordonnée, ce que sont en particulier les ensembles que sont les ordinaux.
Sur une classe
Une classe est un rassemblement d'ensembles qui ne peut sans contradiction être considérée comme un ensemble, comme la classe V de tous les ensembles. Voir classe
Sur une classe bien ordonnée
Sur la classe des ordinaux
Soit F(x) une formule avec pour seule variable libre x, on a alors :
- Théorème : ∀ α { On(α) ⇒ [ ∀ β ( β ∈ α ⇒ F(β) ) ⇒ F(α) ] } ⇒ ∀ γ { On(γ) ⇒ F(γ) }(théorème *)
où On(α) signifie α est un ordinal.
- La démonstration se fait de la manière suivante :
Supposons que : ∀ α { On(α) ⇒ [ ∀ β ( β ∈ α ⇒ F(β) ) ⇒ F(α) ] } (prop. 1)
S'il existait un ordinal α tel qu'on ait pas F(α) alors il en existerait un plus petit (la classe des ordinaux est elle même bien ordonnée par la relation d'appartenance)[1], soit α0 cet ordinal.
Car c'est le plus petit pour tout ordinal β ( β ∈ α0 ⇒ F(β) ) est vrai (car F(β) est vrai ou α0 = l'ensemble vide et (β ∈ α0) est faux). Et donc par l'hypothèse (prop.1) F(α0) est vrai aussi.
Contradiction.
Via en supposant (prop.1) l'hypothèse qu'il existe un ordinal α tel qu'on ait pas F(α) est fausse.
Donc de (prop.1.) découle que pour tout ordinal γ, F(γ). Ce qui est ce qu'il fallait démontrer.
Sur un ensemble
On peut voir un ensemble comme une classe qui appartient à une autre classe.
Sur un ensemble bien ordonné
Voir aussi l'article : Ensemble bien ordonné
Un ensemble A muni d'une relation de bon ordre "<" est une structure d'interprétation (A, <) qui fait de la relation binaire "<" une relation satisfaisant sur A :
- que "<" est une relation d'ordre
- que tout sous ensemble non vide de A a un et un seul plus petit élément pour "<".
Théorème :
- soit B un sous ensemble de A [Plus précisément (B, <) est une sous structure de (A, <)],
- si le plus petit élément de A est élément de B
- et si ∀x ∈ A {(∀y [y < x ⇒ y ∈ B] ) ⇒ (x ∈ B)},
- alors A = B.
Sur un ordinal
On restreint seulement le (théorème *) à un ordinal (ici Ord), ce qui donne :
Soit F(x) une formule avec pour seule variable libre x, et un ordinal Ord on a alors :
∀ α { α ∈ Ord ⇒ [ ∀ β ( β ∈ α ⇒ F(β) ) ⇒ F(α) ] } ⇒ ∀ γ { γ ∈ Ord ⇒ F(γ) }
Utilisation du théorème
Nous nous restreindrons au cas de la classe des ordinaux :
il faut démontrer (prop. 1) à savoir F(α) en supposant F(β) pour tout β appartenant à α.
En général cette preuve se scinde en 3 cas selon que α est 1. l'ensemble vide 2. un ordinal successeur ou 3. un ordinal limite.
Qu'il faille aussi envisager le cas où α est un ordinal limite constitue la nouveauté dans les utilisations du principe de récurrence qui sont présentés dans l'article raisonnement par récurrence sur les seuls entiers.
Définition par récurrence transfinie
Voir aussi le théorème de définissabilité de Beth
Là l'objectif est de définir un objet mathématique par récurrence au delà du fini. Ceci en exhibant une fonction construisant un objet mathématique nouveau à partir d'un autre préalablement défini. Cela passe par la démonstration de l'existence et de l'unicité de la fonction.
Et là encore un théorème dérivé du précédant le permet.
Nous nous restreindrons à ne l'énoncer que pour la classe (mais via valable aussi pour les ensembles) des ordinaux (mais donc aussi généralisable via le théorème de Zermelo à tout ensemble bien ordonné).
Principe de définition par récurrence sur la classe des ordinaux
- Théorème général:
- Soit F(x, y, z) une formule avec x, y, z comme variables libres, telle que :
∀x∀y (On (x) et y est une application de domaine x) ⇒ il existe un unique z tq F(x, y, z)
- Alors il existe une et une seule fonction g, à paramètres dans On, telle que :
Pour tout ordinal α, g(α) est l'unique ensemble u tel que F[α, g|α, u].
( Où "g|α" signifie "g restreint à α", "On(x)" signifie "x est un ordinal" et "On" désigne la classe des ordinaux. )
- Plus simplement :
Soit V la classe de tous les ensembles, et On la classe des ordinaux, on a théorème :
Soit f une fonction de On * V dans V, alors il existe une unique fonction g de On dans V telle que pour tout ordinal α :
- g(α) = f(α, g|α).
( Où "g|α" signifie "g restreint à α", et où f et g correspondent à l'extension de la notion de fonction des ensembles aux classes. )
- On appelle ∈-récursion la généralisation de ce théorème avec f fonction de V * V dans V et g fonction de V dans V.
Construction par récurrence transfinie
Par récurrence transfinie, on peut construire des applications de l'ensemble des ordinaux vers un ensemble E quelconque : c'est-à-dire des sortes de suites. Pour définir une telle "suite" U, il suffit de savoir exprimer U (l'ordinal α) en fonction F de l'ensemble des ordinaux strictement inférieurs à α : bref il suffit de savoir écrire : U(α) = F({U(β),β < α}). L'ordre défini entre ordinaux étant bien fondé, tout ordinal a bien une image par U.
[supposons en effet que ce ne soit pas le cas : soit α1 n'ayant pas d'image par U : si α1 n'est pas le plus petit dans ce cas, soit α2 n'ayant pas d'image par U et strictement plus petit que α1 : si α2 n'est pas le plus petit dans ce cas, soit α3, etc. : la suite des ordinaux αi qu'on construit ici est strictement décroissante : puisque l'ordre entre ordinaux est bien fondé, elle doit avoir une fin : c’est-à-dire qu'on doit trouver un αn qui soit le plus petit ordinal sans image par U. Mais alors pour tout β < αn, une image par U de β est définie : donc F({U(β),β < αn}) peut être définie comme l'image de αn par U : or on vient de dire qu'αn n'avait pas d'image par U : c'est absurde]
Finalement, la définition par récurrence transfinie n'est rien d'autre qu'une définition par récurrence noetherienne sur un ensemble bien ordonné, ici celui des ordinaux (un ordre est un bon ordre si et seulement s'il est total et bien fondé ; la récurrence noetherienne est celle qu'on peut faire sur tout ensemble bien fondé : "si [(pour tout β < α,
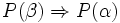 ], alors [pour tout α, P(α)]").
], alors [pour tout α, P(α)]").Articles connexes
Notes
- ↑ Cori et Lascar, Logique mathématique, T.2. Chap.7 §§ 2.6
- Portail des mathématiques
Catégories : Logique mathématique | Raisonnement mathématique
Wikimedia Foundation. 2010.
