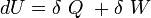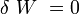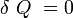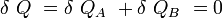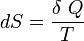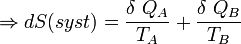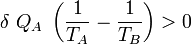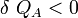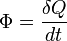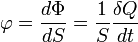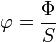- Quantité de chaleur
-
Transfert thermique
 Cet article concerne la notion de chaleur en thermodynamique. Pour les autres sens, voir Chaleur.
Cet article concerne la notion de chaleur en thermodynamique. Pour les autres sens, voir Chaleur.Un transfert thermique, appelé plus communément chaleur[1], est un transfert d'énergie microscopique désordonnée. Cela correspond en réalité à un transfert d'agitation thermique entre particules, au gré des chocs aléatoires qui se produisent à l'échelle microscopique.
L'exemple le plus courant de situation mettant en jeu un transfert thermique est le système constitué de deux corps en contact et ayant des températures différentes. Le corps le plus chaud cède de l'énergie sous forme de chaleur au corps le plus froid. Il y a transfert thermique entre les deux corps. Il peut se produire des transferts thermiques vers un système dont la température reste constante, par exemple dans le cas d'un changement d'état physique (exemple : la fusion de la glace à 0°C sous la pression atmosphérique).
L'étude de ces transferts s'effectue dans le cadre de la discipline thermodynamique en s'appuyant sur les deux premiers principes.
À la différence de la thermodynamique, la thermocinétique fournit des informations sur le mode de transfert en situation de non équilibre ainsi que sur les valeurs de flux de chaleur.
Sommaire
Historique et évolution de la terminologie
La chaleur, dans le langage commun, est souvent confondue avec la notion de température. Bien que strictement différentes d'un point de vue scientifique, les deux notions sont en effet reliées entre elles et l'histoire même de la genèse de la thermodynamique a parfois induit cette confusion.
Au XIXe siècle, la chaleur est assimilée à un fluide : le calorique. Les progrès et les succès de la calorimétrie imposent cette théorie jusqu'à la fin du XIXe siècle. Cette conception est en effet reprise par Sadi Carnot : un moteur thermique ne peut fonctionner que si la chaleur circule d'un corps dont la température est plus élevée vers un corps dont la température est plus faible ; raisonnement correspondant à une analogie avec une machine hydraulique qui tire son énergie du passage de l'eau d'un réservoir d'altitude élevée vers un réservoir d'altitude inférieure.
Ce n'est qu'avec l'avènement de la thermodynamique statistique que la chaleur sera définie comme un transfert de l'agitation thermique des particules au niveau microscopique. Un système dont les particules sont statistiquement plus agitées présentera une température d'équilibre, définie à l'échelle macroscopique, plus élevée. La température est donc une grandeur macroscopique qui est le reflet statistique des énergies cinétiques des particules à l'échelle microscopique. Au cours de chocs aléatoires, les particules les plus agitées transmettent leurs énergies cinétiques aux particules les moins agitées. Le bilan de ces transferts d'énergies cinétiques microscopiques correspond à la chaleur échangée entre des systèmes constitués de particules dont l'agitation thermique moyenne est différente.
La température est donc une fonction d'état intensive servant à décrire l'état d'équilibre d'un système alors que la chaleur est un transfert d'agitation thermique assimilable à une quantité d'énergie, associé à l'évolution d'un système entre deux états distincts ou identiques si la transformation est cyclique.
Chaleur et thermodynamique
Évolution de deux corps en contact
 Transfert d'énergie d'agitation thermique par choc.
Transfert d'énergie d'agitation thermique par choc.
Soient deux objets A et B indéformables dans un système parfaitement isolé thermiquement et mécaniquement, ayant les caractéristiques suivantes :
Objet A Objet B Volume VA Volume VB Température TA (TA > TB) Température TB Masse mA Masse mB Chaleur spécifique cpA Chaleur spécifique cpB Dans ce cas le sens du transfert thermique est gouverné par la différence de température entre les deux corps. L’expérience montre que c’est le corps chaud qui cède de l’énergie au corps froid de façon à ce que, à l’équilibre, les températures des deux corps soient identiques.
Conformément au premier principe de la thermodynamique, nous pouvons écrire que l’énergie interne est égale à la somme de la chaleur et du travail :
- Les objets sont indéformables donc :
- Le système est isolé donc :
Si δQA et δQB sont respectivement les énergies thermiques élémentaires échangées entre l’objet A et l’objet B, faisant partie du système isolé.
D’où :
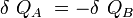
Le deuxième principe de la thermodynamique permet d’écrire la relation suivante liant les entropies des objets A et B :
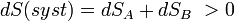 , puisque le système est isolé.
, puisque le système est isolé.
par définition.
Nous pouvons écrire :
Si : TA > TB
Cela signifie que :
et donc que :
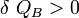
D’après la règle des signes, on conclut que l’objet A cède de la chaleur à l’objet B. L’objet le plus chaud cède donc de la chaleur à l’objet le plus froid.
Le premier principe et la chaleur
Le premier principe de la thermodynamique est un principe de conservation de l'énergie. Il introduit la fonction d'état énergie interne U .
Au cours d'une transformation d'un système thermodynamique fermé, entre deux états I et F la variation de l'énergie interne U(F) - U(I) est due à la somme :
- des travaux macroscopiques réalisés
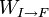 , en général le travail des forces de pression.
, en général le travail des forces de pression. - des transferts d'énergies microscopiques ou chaleurs,
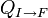 .
.
Ce qui se traduit par :
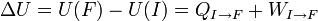
On en déduit donc une définition formelle de la chaleur le long d'un chemin bien défini allant de I à F :
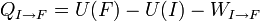
L'intégrale curviligne permettant le calcul du travail des forces de pression:
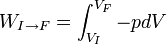 , n'est pas indépendante du chemin suivi pour aller de I vers F car le travail n'est pas une fonction d'état.
, n'est pas indépendante du chemin suivi pour aller de I vers F car le travail n'est pas une fonction d'état.Il s'ensuit également que la chaleur n'est pas une fonction d'état et donc qu'elle dépend du chemin suivi. Notamment si la transformation permettant d'amener un corps d'un état I à un état F est réalisée de deux façons différentes, les chaleurs mises en jeu sont également a priori différentes.
Néanmoins dans certaines conditions expérimentales, la chaleur mise en jeu est égale à la variation d'une fonction d'état. C'est le cas pour une transformation d'un système fermé, effectuée à volume constant : la chaleur est égale à la variation d'énergie interne : ΔU = QV. Dans le cas d'une transformation à pression constante la chaleur est égale à la variation d'enthalpie : ΔH = QP . Ces deux propriétés sont mises à profit dans le domaine de la calorimétrie effectuée dans un calorimètre fonctionnant soit à pression constante soit à volume constant dans le cas d'une bombe calorimétrique.
Le second principe et la chaleur
Le second principe de la thermodynamique est un principe d'évolution. Il introduit la fonction d'état entropie qui est une mesure du désordre de la matière. La fonction entropie est définie à l'échelle macroscopique de telle sorte que sa variation au cours de la transformation réversible d'un système correspond au rapport de la quantité de chaleur échangée avec le milieu extérieur sur la température du système :
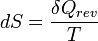
d'où :
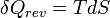
Et pour une transformation finie à température T constante, allant d'un état I à un état F d'équilibre :
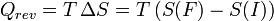
La chaleur est donc associée à une variation d'entropie. Or, plus il y a création d'entropie, plus la transformation est irréversible et plus le travail utile récupéré sera faible : ceci justifie le qualificatif donné à la chaleur d'être une dégradation qualitative de l'énergie ( voir le deuxième principe de la thermodynamique).
Exemples de calcul de chaleur mise en jeu, au cours d'une transformation affectant un corps pur
Les grandeurs thermodynamiques associées à une quantité déterminée de corps pur ( n constant ) ne dépendent que de deux variables indépendantes.
Deux fonctions d'état introduites par le premier principe sont reliées à la chaleur sous certaines contraintes: V=cte ou P=cte.
- À volume constant on choisit la fonction d'état énergie interne.
Car à volume constant la variation de la fonction énergie interne d'un corps pur est égale à la chaleur échangée avec le milieu extérieur.
Fonction d'état énergie interne: U(T,V)
Sa différentielle est égale à:
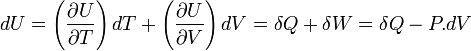
Si V = cte
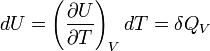
la grandeur
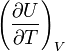 est la capacité calorifique molaire à volume constant, appelée
est la capacité calorifique molaire à volume constant, appelée 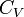 et qui s'exprime en J.K-1.mol-1.
et qui s'exprime en J.K-1.mol-1.La chaleur mise en jeu pour une mole est donc égale à:
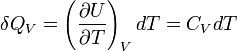
Pour n moles
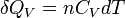
Enfin pour une transformation isochore allant de l'état A défini par TA à un état B défini par TB
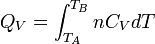
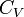 est fonction de T. Mais si l'intervalle de T n'est pas trop grand ( quelques dizaines voire centaines de degrés), on peut la considérer en première approximation comme constante.
est fonction de T. Mais si l'intervalle de T n'est pas trop grand ( quelques dizaines voire centaines de degrés), on peut la considérer en première approximation comme constante.d'où:
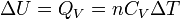
- À pression constante on choisit la fonction d'état enthalpie.
Car à pression constante la variation de la fonction enthalpie d'un corps pur est égale à la chaleur échangée avec le milieu extérieur.
Fonction d'état enthalpie: H(T,P)
Sa différentielle est égale:
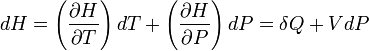
Si P = cte
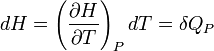
la grandeur
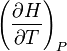 est la capacité calorifique molaire à pression constante, appelée
est la capacité calorifique molaire à pression constante, appelée 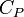 et qui s'exprime en J.K-1.mol-1.
et qui s'exprime en J.K-1.mol-1.La chaleur mise en jeu pour une mole est donc égale à:
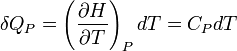
Pour n moles
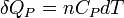
Enfin pour une transformation isobare allant de l'état A défini par TA à un état B défini par TB
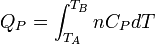
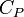 est fonction de T. Mais si l'intervalle de T n'est pas trop grand ( quelques dizaines voire centaines de degrés), on peut la considérer en première approximation comme constante.
est fonction de T. Mais si l'intervalle de T n'est pas trop grand ( quelques dizaines voire centaines de degrés), on peut la considérer en première approximation comme constante.d'où:
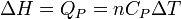
- Cas du changement d'état physique.
Généralement on considère le changement d'état physique effectué à l'air libre c'est à dire à pression constante (pression atmosphérique). Tout le monde sait que la glace fond à 0°C sous la pression atmosphérique et tant qu'il y a coexistence de la glace et de l'eau liquide, la température reste constante. Le changement d'état d'un corps pur s'effectue donc à P = Cte et T = Cte. La chaleur mise en jeu correspond donc à une variation d'enthalpie: ΔH puisque la pression est constante. On l'appelle encore chaleur latente molaire de changement d'état: L.
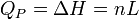
Les modes de transferts thermiques
Il y existe trois modes de transfert :
- Conduction : l'énergie passe d'un corps à un autre, par contact.
- Convection : un corps qui se déplace emmène avec lui, l'énergie qu'il contient. La quantité d'énergie ainsi transportée peut être importante, notamment dans le cas d'un changement de phase.
- Rayonnement (radiation) : tous les corps émettent de la lumière, en fonction de leur température, et sont eux-mêmes chauffés par la lumière qu'ils absorbent.
Résumé des modes de transfert Mode de transfert Échelle Éléments nécessaires Conduction Microscopique Contact entre deux matières, gradient de température Convection Macroscopique Matière libre (possibilité de mouvement, souvent un fluide), gradient de température Rayonnement (radiation) Microscopique Aucun : peut se faire dans le vide ou la matière, quelle que soit la température (à partir de 0 K). Conduction
Article détaillé : Conduction thermique.Le transfert par conduction est un échange d'énergie avec contact quand il existe un gradient de température ( variation progressive de la température) au sein d'un système.
Dans un gaz ou un liquide, l'énergie se propage par contact direct entre molécules au gré des chocs aléatoires à l'échelle microscopique. Dans un solide ou fluide immobilisé, la vibration des atomes autour de leur position d'équilibre dans le solide, se transmet de proche en proche. Les cristaux disposent d'un mode de transfert thermique supplémentaire particulier associé aux vibrations du réseau (voir phonon).
Exemples de transfert par conduction : transfert à travers une paroi diathermique (par exemple les ailettes de refroidissement d'un moteur ou les radiateurs d'un chauffage central...) contrairement à une paroi adiabatique qui s'oppose au transfert de chaleur (par exemple, la paroi d'une bouteille thermos).
D'une manière simple,le flux de chaleur qui passe dans un solide de manière monodirectionnel s'exprime de la manière suivante :
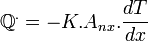
Où
- Q. : flux de chaleur (se lit « Q point ») ;
- K : conductibilité thermique du matériau déterminée expérimentalement (en W.m − 1.K − 1) ;
- Anx = Surface perpendiculaire au flux de chaleur (normal à l'axe x considéré) ;
- T : température (en kelvin) ;
- x : axe considéré.
Convection
Article détaillé : Convection.Définition : transfert d'énergie qui s'accompagne de mouvement de molécules dans un fluide (liquide ou gaz).
-
- Convection naturelle (ou libre) : l'échange de chaleur est responsable du mouvement. Le transfert thermique provoque le mouvement.
- Convection forcée : un dispositif mécanique entraine les molécules vers le dispositif chauffant. Le mouvement favorise le transfert thermique.
Les lois sont très différentes dans les deux cas.
Exemples de transfert par convection: échange de chaleur dans des radiateurs à circulation d'eau ou d'air (convection forcée), refroidissement d'une tasse de liquide chaud en soufflant dessus (convection forcée), diffusion de l'air chaud au-dessus d'un radiateur électrique (convection naturelle s'il n'y a pas de soufflerie dans le radiateur).
Convection naturelle Convection forcée Rayonnement
Définition : Le transfert se fait par rayonnement électromagnétique (par exemple : infrarouge). Le transfert peut se réaliser dans le vide sans la présence de matière. L'exemple caractéristique de ce type de transfert est le rayonnement du soleil dans l'espace.
Exemples de transfert par rayonnement : système de chauffage dit par radiant ; le soleil.
La loi de Stefan-Boltzmann (ou loi de Stefan) permet de quantifier ces échanges. La puissance rayonnée par un corps est donnée par la relation :
- P = εSσT4
avec
- σ : constante de Stefan-Boltzmann (5,6703 . 10-8 W.m-2.K-4)
- ε : émissivité, coefficient sans unité qui vaut 1 pour un corps noir et qui est compris entre 0 et 1 selon l’état de surface du matériau.
- S : superficie du corps ;
- T : température du corps (en kelvin).
Si le corps récepteur réfléchit certaines longueurs d'ondes ou est transparent à d'autres, seules les longueurs d'onde absorbées contribuent à son équilibre thermique. Si par contre le corps récepteur est un corps noir, c'est-à-dire qu'il absorbe tous les rayonnements électromagnétiques, alors tous les rayonnements contribuent à son équilibre thermique.
Combinaison des modes de transfert
Le transfert d'énergie par chaleur se réalise généralement par une combinaison de plusieurs modes.
Par exemple, le système chauffage central, combine la convection (en général forcée) pour chauffer le fluide dans la chaudière, la conduction pour chauffer les parois du radiateur et la convection (en général naturelle) pour chauffer l'air autour du radiateur. Dans le cas du chauffage d'un solide par radiation, la transmission de chaleur sera une combinaison de radiation et de conduction. C'est le cas du verre d'une vitre chauffée par le rayonnement solaire; le transfert étant combiné avec une convection naturelle de l'air, derrière la vitre d'une pièce.
Parfois le transfert thermique s'accompagne d'un transfert de matière. Par exemple dans le cas de l'ébullition d'un liquide, une partie du liquide subit un changement d'état physique et le gaz ainsi créé se sépare du liquide.
Grandeurs physiques
Flux thermique
Le flux thermique est la quantité d'énergie thermique qui traverse une surface isotherme par unité de temps. Il est appelé « puissance thermique » pour les équipements thermiques tels que les radiateurs.
Le flux s'exprime en :
Densité de flux thermique
La densité de flux thermique (ou flux thermique surfacique) c'est le flux thermique par unité de surface. La densité de flux thermique s'exprime en watt par mètre carré (W.m-2).
Si la densité de flux est uniforme sur la surface considérée :
Notes et références
- ↑ S. Olivier et H. Gié, Thermodynamique, Lavoisier Tec&Doc, Paris, 1998, page 133 : « Un tel transfert d'énergie est appelé chaleur ou mieux transfert thermique et noté Q » ; avec un appel de note de bas de page qui explique : « Le mot chaleur est de loin le plus utilisé : c'est un héritage légué par les fondateurs de la thermodynamique, et qui s'impose par sa simplicité. L'usage courant de formules telles que l'eau est chaude confère au mot chaleur une ambiguïté regrettable : on sous-entend ainsi que la chaleur est une forme d'énergie stockée par l'eau, alors que la chaleur n'est qu'une forme d'échange d'énergie. »
Voir également
Articles connexes
- Physique statistique
- Conduction thermique
- Convection
- Corps noir
- Gradient
- Température
- Isolant
- Premier principe de la thermodynamique
- Second principe de la thermodynamique
- Entropie
- Chaleur latente
- Chaleur sensible
- Transferts thermiques dans le bâtiment
Liens externes
- Portail de la physique
Catégorie : Transfert thermique
Wikimedia Foundation. 2010.