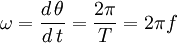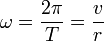- Pulsation
-
Vitesse angulaire
 Pour les articles homonymes, voir pulsation (homonymie).
Pour les articles homonymes, voir pulsation (homonymie).En physique, et plus spécifiquement en mécanique, la vitesse angulaire ω, aussi appelée fréquence angulaire ou pulsation, est une mesure de la vitesse de rotation. Elle s'exprime dans le système international en radians par seconde (rad.s-1), ou plus simplement en s-1 puisque les angles sont des grandeurs sans dimension ; elle reste de manière courante donnée en tours par minute (tr/min). Une révolution complète est égale à 2π radians, donc :
où l'expression
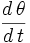 est la dérivée de l'angle par rapport au temps (en rad.s-1), T est la période de rotation (en s) et f est la fréquence (en s-1).
est la dérivée de l'angle par rapport au temps (en rad.s-1), T est la période de rotation (en s) et f est la fréquence (en s-1).L'utilisation de la vitesse angulaire au lieu de la fréquence ordinaire est pratique dans maintes applications car elle permet d'éviter l'apparition excessive de π. Elle est utilisée, entre autres, dans de nombreux domaines de la physique comme la mécanique quantique et l'électromagnétisme ainsi qu'en mathématiques pour la transformée de Fourier.
Pour une trajectoire circulaire:
T est la période (en s), r est le rayon de la rotation (en m) et v est la vitesse du point (en m.s-1)
On utilise parfois un vecteur vitesse angulaire
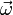 . Il s'agit du vecteur :
. Il s'agit du vecteur :- normal au plan de rotation,
- orienté de sorte que le mouvement se fasse dans le sens positif,
- et dont la norme vaut ω.
Sommaire
Théorèmes et propriétés relatifs à la fréquence angulaire
Composition des vitesses angulaires
Quels que soient les solides A, B et C, les fréquences de rotations sont liées par :
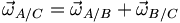 . Remarque: il ne s'agit pas vraiment de vecteur puisque le symétrique dans un miroir est inversé.
. Remarque: il ne s'agit pas vraiment de vecteur puisque le symétrique dans un miroir est inversé.- Exemple
- Soit un Référentiel galiléen R.
Considérons un solide S1 en rotation à la fréquence angulaire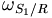 , par rapport au référentiel R.
, par rapport au référentiel R.
Considérons également un solide S2 en rotation par rapport à S1 à la fréquence angulaire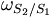 .
.
La vitesse de rotation de S2 par rapport à R,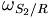 sera égale à
sera égale à 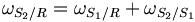 .
.
Dans ce cas, si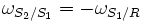 , le solide S2 sera en translation circulaire dans le référentiel R.
, le solide S2 sera en translation circulaire dans le référentiel R.
Relation Vitesse - Fréquence angulaire
Soient un solide S, et A et B, deux points de ce solide. Alors les vitesses des points A et B sont reliées par la relation suivante :
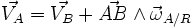
cette formule montre bien que « ω » (omega - en rad.s-1) n'est pas une vitesse (en m.s-1). Mais
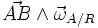 est bien homogène à une vitesse.
est bien homogène à une vitesse.- Exemple
- Soit un disque de 1m de rayon, en rotation autour de son axe de symétrie à la vitesse ωD / R (R un référentiel galiléen). Si ω est exprimée en radians par secondes, alors chacun des points situés sur le bord du disque aura une vitesse, dite aussi vitesse linéaire, orthogonale à l'axe de rotation (par propriété du produit vectoriel) de
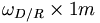 . Unité : mètres par seconde.
. Unité : mètres par seconde.
Centre instantané de rotation
Par analogie : lorsqu'un mouvement n'est pas rectiligne, on peut regarder de façon ponctuelle sa vitesse et sa direction à un instant donné. De la même façon, s'il n'est pas en rotation, on peut considérer de façon ponctuelle une vitesse angulaire et un centre de rotation.
Le centre instantané de rotation de A par rapport à B, pour l'instant t est le point I de A vérifiant :
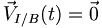
Voir aussi
- Portail de la physique
Catégories : Grandeur physique | Mécanique
Wikimedia Foundation. 2010.