Propriete de Church-Rosser
- Propriete de Church-Rosser
-
Propriété de Church-Rosser
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Propriete de Church-Rosser de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Propriété de church-rosser — Soit R un système de réécriture. Notons la relation de réduction, sa clôture réflexive et transitive, ainsi que sa clôture réflexive, transitive et symétrique. On dit que R a la propriété de Church Rosser si pour tous les termes M1,M2 tels … Wikipédia en Français
Propriété de Church-Rosser — Soit R un système de réécriture. Notons la relation de réduction, sa clôture réflexive et transitive, ainsi que sa clôture réflexive, transitive et symétrique. On dit que R a la propriété de Church Rosser … Wikipédia en Français
Alonzo Church — Pour les articles homonymes, voir Alonzo et Church. Alonzo Church Naissance 14 juin 1903 Washington, D.C., (États Unis) Décès 11 août … Wikipédia en Français
Systeme F — Système F Pour les articles homonymes, voir System F (homonymie). Le système F (également connu sous le nom de lambda calcul polymorphe ou de lambda calcul du second ordre) est une extension du lambda calcul simplement typé introduite… … Wikipédia en Français
Système F — Pour les articles homonymes, voir System F (homonymie). Le système F (également connu sous le nom de lambda calcul polymorphe ou de lambda calcul du second ordre) est une extension du lambda calcul simplement typé introduite indépendamment par le … Wikipédia en Français
Reecriture (informatique) — Réécriture (informatique) Pour les articles homonymes, voir Réécriture. La réécriture (ou récriture) est un modèle de calcul utilisé en informatique, en algèbre, en logique mathématique et en linguistique. Il s’agit de transformer des objets… … Wikipédia en Français
Réécriture (arithmétique) — Réécriture (informatique) Pour les articles homonymes, voir Réécriture. La réécriture (ou récriture) est un modèle de calcul utilisé en informatique, en algèbre, en logique mathématique et en linguistique. Il s’agit de transformer des objets… … Wikipédia en Français
Système de réécriture — Réécriture (informatique) Pour les articles homonymes, voir Réécriture. La réécriture (ou récriture) est un modèle de calcul utilisé en informatique, en algèbre, en logique mathématique et en linguistique. Il s’agit de transformer des objets… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Réécriture (informatique) — Pour les articles homonymes, voir Réécriture. La réécriture (ou récriture) est un modèle de calcul utilisé en informatique, en algèbre, en logique mathématique et en linguistique. Il s’agit de transformer des objets syntaxiques (mots, termes,… … Wikipédia en Français
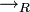 la relation de réduction,
la relation de réduction, 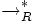 sa clôture réflexive et transitive, ainsi que
sa clôture réflexive et transitive, ainsi que 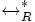 sa clôture réflexive, transitive et symétrique.
sa clôture réflexive, transitive et symétrique.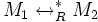 , il existe un terme M' tel que
, il existe un terme M' tel que 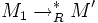 et
et 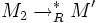 .
.