- Preuve par l'absurde
-
Raisonnement par l'absurde
Le raisonnement par l'absurde (du latin reductio ad absurdum) ou apagogie (du grec ancien apagôgê) est une forme de raisonnement logique, philosophique, scientifique consistant soit à démontrer la vérité d'une proposition en prouvant l'absurdité de la proposition complémentaire (ou « contraire »), soit à montrer la fausseté d'une autre proposition en en déduisant logiquement des conséquences absurdes.
Sommaire
Apagogie positive
On parle d'apagogie positive ou de démonstration par l'absurde simple quand la conclusion affirme la vérité d'une proposition, non en l'établissant directement par une démonstration tirée de la nature même de la chose, mais indirectement, en faisant voir que la proposition contraire est absurde. On conclut de la fausseté de l'une à la vérité de l'autre.
Par exemple, Spinoza démontre par l'absurde que « la production d'une substance est chose absolument impossible » (Éthique I, proposition VI, corollaire). En effet, si une substance pouvait être produite, la connaissance de cette substance devrait dépendre de la connaissance de sa cause (sachant que la connaissance de l'effet suppose celle de la cause) et ainsi elle ne serait plus une substance, puisqu'une substance est précisément ce qui est en soi et est conçu par soi.
Limites de ce mode de raisonnement
Ce raisonnement n'est légitime que lorsqu'il n'y a que deux propositions contradictoires possibles, dont l'une est nécessairement fausse si l'autre est vraie, et réciproquement ; autrement il dégénère en sophisme s'appuyant sur un faux dilemme. Ou alors, il faut effectivement prouver la fausseté de toutes les autres thèses alternatives : soit A, B ou C considérées comme hypothèses possibles, on prouve que B et C sont fausses, A est donc vraie (il s'agit classiquement de ce qu'on appelle aussi le raisonnement disjonctif (modus tollendo-ponens).
D'un point de vue épistémologique, cette preuve reste toujours inférieure à la démonstration directe, parce que, si elle contraint l'esprit, elle ne l'éclaire pas et ne donne pas la raison des choses, comme le fait la preuve directe ou ostensive. Il est donc préférable de ne l'employer que quand on ne peut faire autrement : si, par exemple, dans la discussion, on a affaire à un contradicteur qui se refuse à toute preuve directe ou qui nie les principes. C'est le cas pour la réfutation de certaines doctrines, comme le scepticisme.
Application en mathématiques
La démonstration par l'impossible, usitée dans les mathématiques pour démontrer certains théorèmes rentre dans la preuve apagogique ; elle n'est pas admise par certains mathématiciens dits intuitionnistes, qui rejettent le principe du tiers exclu.
Admettons que nous ayons à démontrer une proposition p. La démarche consiste à montrer que l'hypothèse non p (i.e. que p est fausse) mène à une contradiction logique. Ainsi p ne peut pas être fausse et doit être donc vraie.
Prenons un exemple simple et considérons la proposition « il n'y a pas de plus petit nombre rationnel strictement plus grand que 0 ». Dans un raisonnement par l'absurde, nous commençons par prendre la négation de la proposition : « il existe un plus petit nombre rationnel strictement positif, disons r0 ».
Maintenant soit x = r0/2. Alors x est un nombre rationnel, x est strictement plus grand que 0 et x est strictement plus petit que r0. Mais cela est absurde - contradictoire avec notre hypothèse initiale que r0 était le plus petit nombre rationnel. Ainsi nous pouvons conclure que la proposition d'origine est nécessairement vraie : il n'y a pas de plus petit nombre rationnel strictement plus grand que 0.
Il n'est pas rare d'utiliser ce type d'argument avec des propositions telles que celle ci-dessus, pour démontrer la non-existence de quelque objet mathématique. Nous supposons que de tels objets existent et ensuite nous démontrons que cela nous mène à une contradiction ; ainsi, de tels objets n'existent pas. Pour des exemples, voyez la démonstration que la racine carrée de 2 est irrationnelle et la démonstration de la non dénombrabilité de l'ensemble des réels de Cantor (il faut cependant remarquer que, pour les raisons exposées au prochain paragraphe, les mathématiciens se sont efforcé d'obtenir des preuves directes, et qu'en particulier le raisonnement par l'absurde figurant dans la preuve du théorème de Cantor peut facilement être éliminé).
Mise en garde
Pour fournir une preuve valide, il doit être démontré que pour une proposition donnée p, non p implique une propriété qui est réellement fausse dans le système mathématique utilisé. Le danger ici est d'utiliser un sophisme, où nous montrons que non p implique une propriété q, qui semble fausse, mais qui n'est pas vraiment démontrée comme fausse. Les exemples historiques de cette erreur abondent, parmi lesquels la démonstration erronée du cinquième postulat d'Euclide (aussi connu comme le postulat de la parallèle) à partir des autres postulats. L'échec de ces démonstrations a par la suite mené aux géométries non euclidiennes.
Bien que l'on doive toujours préférer une démonstration directe, le raisonnement par l'absurde est assez couramment employé dans les démonstrations mathématiques fondées sur la logique classique. Les mathématiciens intuitionnistes récusent ce type de raisonnement, en même temps qu'ils récusent le tiers exclu, car pour eux, la démonstration que l'ajout de
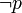 conduit à une contradiction ne permet pas de construire une démonstration de p, mais seulement de
conduit à une contradiction ne permet pas de construire une démonstration de p, mais seulement de 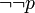 , qui est plus faible.
, qui est plus faible.En calcul des propositions, la reductio ad absurdum est représentée grosso modo par :
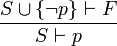
Dans ce qui précède,
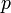 est la proposition que nous souhaitons démontrer et
est la proposition que nous souhaitons démontrer et 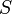 est un ensemble d'assertions qui sont données comme vraies ; celles-ci pourraient être, par exemple, les axiomes de la théorie dans laquelle nous travaillons ou des hypothèses spécifiques. Nous considérons la négation de
est un ensemble d'assertions qui sont données comme vraies ; celles-ci pourraient être, par exemple, les axiomes de la théorie dans laquelle nous travaillons ou des hypothèses spécifiques. Nous considérons la négation de 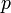 en plus de
en plus de 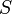 ; si ceci mène à une contradiction logique
; si ceci mène à une contradiction logique 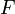 , alors nous pouvons conclure que des propositions de
, alors nous pouvons conclure que des propositions de 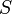 on déduit
on déduit 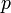 .
.Apagogie négative
En philosophie, la méthode apagogique ou réduction à l'absurde a une place plus importante dans le domaine de la réfutation des idées adverses. L'apagogie consiste alors à faire ressortir que la proposition à réfuter conduit à des conséquences absurdes car impossibles (contradictoires avec elles-mêmes ou avec d'autres principes admis comme vrais). Moins risqué que l'apagogie positive, ce mode de raisonnement n'affirme pas forcément que l'inverse est vraie. Ainsi, on réfutera par exemple la proposition tout ce qui est rare est cher en indiquant que si c'était vrai, alors il s’ensuivrait qu’un cheval bon marché, qui est chose rare, devrait en même temps être cher, ce qui est absurde, c’est-à-dire contradictoire dans les termes. La proposition « tout ce qui est rare est cher » est donc nécessairement fausse. Mais on n'affirme pas pour autant que "tout ce qui se trouve facilement est cher" ou que "tout ce qui est rare est bon marché" (propositions qui ne sont toutefois pas inverses de "tout ce qui est rare est cher" : l'inverse de cette proposition est "Il existe des choses qui sont rares sans être chères") !
Moins rigoureusement, voire de façon sophistique, on se contentera de faire ressortir des conséquences funestes ou désagréables d'une thèse ou d'une doctrine (voir l'argumentum ad consequentiam).
Néanmoins, il reste aussi préférable d'un point de vue logique de réfuter par l'analyse directe de la fausseté des principes. Aussi un usage non critique de ce type de preuve peut-il être soupçonné d'appartenir plus à la dialectique éristique et à la rhétorique qu'à la philosophie proprement dite.
Catégories : Raisonnement mathématique | Rhétorique | Méthode de démonstration
Wikimedia Foundation. 2010.
