- Polynôme d'appell généralisé
-
Polynôme d'Appell généralisé
Sommaire
Définition
En mathématiques, une suite de polynômes
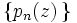 possède une représentation d'Appell généralisée si la fonction génératrice des polynômes prend la forme suivante :
possède une représentation d'Appell généralisée si la fonction génératrice des polynômes prend la forme suivante :où la fonction génératrice
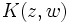 est composée des séries :
est composée des séries :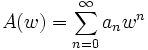 avec
avec 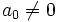
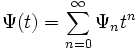 avec tous les
avec tous les 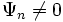
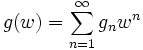 , avec
, avec 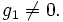
Dans les conditions ci-dessus, il n'est pas difficile de montrer que
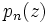 est un polynôme de degré
est un polynôme de degré 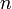 .
.Cas particuliers
- Le choix de
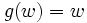 donne la classe des polynômes de Brenke.
donne la classe des polynômes de Brenke.
- Le choix de
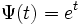 donne la suite des polynômes de Sheffer.
donne la suite des polynômes de Sheffer.
- Le choix simultané de
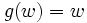 et de
et de 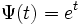 donne la suite des polynômes d'Appell au sens strict.
donne la suite des polynômes d'Appell au sens strict.
Représentation explicite
Les polynômes d'Appell généralisés ont la représentation explicite
Le coefficient
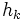 est
estoù la somme s'étend à toutes les partitions de n en k+1 parties — au sens large — c'est-à-dire en admettant la partie vide pour
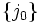 ; si bien que la somme comprend tous les
; si bien que la somme comprend tous les 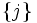 , nuls ou non, tels que
, nuls ou non, tels que  .
.Pour les polynômes d'Appell, ceci devient la formule :
Relations de récurrence
De manière équivalente, une condition nécessaire et suffisante pour que le noyau
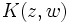 puisse être écrit comme
puisse être écrit comme 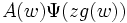 avec
avec 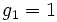 est que
est queoù
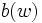 et
et 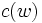 ont un développement en série
ont un développement en sérieet
En faisant la substitution :
il vient immédiatement la relation de récurrence :
Dans le cas particulier des polynômes de Brenke, on a
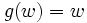 et donc tous les
et donc tous les 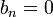 , ce qui simplifie considérablement la relation de récurrence.
, ce qui simplifie considérablement la relation de récurrence.Références
- Ralph P. Boas, Jr. and R. Creighton Buck, « Polynomial Expansions of Analytic Functions » (Deuxième édition corrigée), (1964) Academic Press Inc., Publishers, New York, Springer-Verlag, Berlin. Library of Congress Card Number 63-23263.
- William C. Brenke, On generating functions of polynomial systems, « American Mathematical Monthly », (1945) 52 pp. 297-301.
- W. N. Huff, The type of the polynomials generated by f(xt) φ(t) « Duke Mathematical Journal », (1947) 14 pp 1091-1104.
- Portail des mathématiques
Catégorie : Polynôme remarquable
Wikimedia Foundation. 2010.

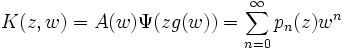
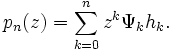
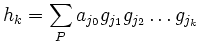
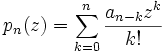
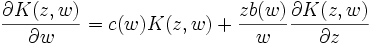
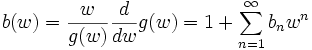
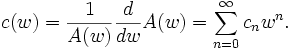
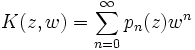
![z^{n+1} \frac {d}{dz} \left[ \frac{p_n(z)}{z^n}
\right]= -\sum_{k=0}^{n-1} c_{n-k-1} p_k(z) -z \sum_{k=1}^{n-1} b_{n-k} \frac{d}{dz} p_k(z)](/pictures/frwiki/55/70cc9c66c85f05c73da0273938cd9410.png)