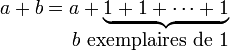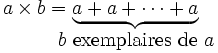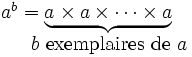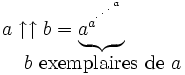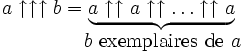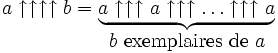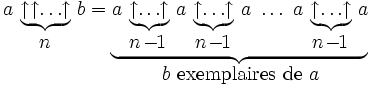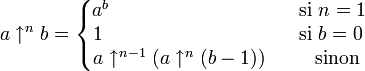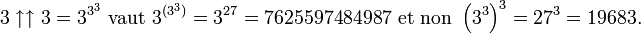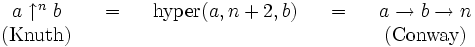Notation de puissance de Knuth

Notation des puissances itérées de Knuth

En mathématiques, la notation des puissances itérées de Knuth est une notation qui permet d'écrire de très grands entiers et qui a été introduite par Donald Knuth en 1976. L'idée de cette notation est basée sur la notion d'exponentiation répétée, au même titre que l'exponentiation consiste en une multiplication itérée ou la multiplication en une addition itérée.

Introduction

Itération d'une fonction simple

Les itérations d'une fonction simple sont utilisées de manière classique en arithmétique pour définir les opérations de plus en plus complexes. À partir de la fonction "successeur", qui permet de construire les entiers naturels par incrémentations successives, l'addition peut ainsi être définie comme une incrémentation itérée :

$\begin{matrix} a + b=a+\underbrace{1_{}+1+\dots+1}\\ \qquad\quad\ \ b\mbox{ exemplaires de }1 \end{matrix}$

ou encore, sous forme de programme itératif à partir de l'incrémentation :

function Addition(a, b: Naturel) : Naturel
begin
R := a
(* Application b fois de l'opérateur à gauche "1+" *)
for compteur:=1 to b do R:=1+R
return R
end.

La multiplication peut de même être définie comme une addition itérée :

$\begin{matrix} a\times b=\underbrace{a_{}+a+\dots+a}\\ \qquad\quad\ \ b\mbox{ exemplaires de }a \end{matrix}$

ou encore, sous forme de programme itératif à partir de l'addition:

function Multiplication(a, b: Naturel) : Naturel
begin
R := 0 (* élément neutre pour l'addition *)
(* Application b fois de l'opérateur à gauche "a+" *)
for compteur:=1 to b do R:=a+R
return R
end.

De même, l'exponentiation peut être définie comme une multiplication itérée :

$\begin{matrix} a^b=\underbrace{a_{}\times a\times\dots\times a}\\ \qquad\ b\mbox{ exemplaires de }a \end{matrix}$

ou encore, sous forme de programme itératif à partir de la multiplication:

function Puissance(a, b: Naturel) : Naturel
begin
R := 1 (* élément neutre pour la multiplication*)
(* Application b fois de l'opérateur à gauche "a*" *)
for compteur:=1 to b do R:=a*R
return R
end.

Généralisation

À partir de l'incrémentation, les itérations successives conduisent ainsi à définir les opérateurs d'addition, de multiplication, et d'exponentiation. Cela a inspiré Knuth pour définir un opérateur double flèche pour une exponentiation itérée :

$\begin{matrix} a\uparrow\uparrow b=\underbrace{a_{}^{a^{{}^{.\,^{.\,^{.\,^a}}}}}}\\ \qquad\quad\ \ \ b\mbox{ exemplaires de }a \end{matrix}$

ou encore, sous forme de programme itératif à partir de la fonction puissance:

function 2_Puissance(a, b: Naturel) : Naturel
begin
R := 1 (* élément neutre pour la fonction puissance*)
(* Application b fois de l'opérateur à gauche "a^" *)
for compteur:=1 to b do R:=a ^ R
return R
end.

D'après cette définition,

$3\uparrow\uparrow2=3^3=27\,\!$

$3\uparrow\uparrow3=3^{3^3}=3^{27}=7625597484987\,\!$

$3\uparrow\uparrow4=3^{3^{3^3}}=3^{7625597484987}\,\!$

$3\uparrow\uparrow5=3^{3^{3^{3^3}}}\,\!$

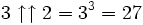
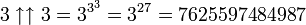
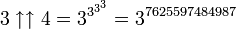
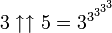
etc.

Même si cela permet déjà d'écrire de très grands nombres, Knuth ne s'est pas arrêté là. Il a poursuivi en définissant l'opérateur triple flèche comme l'application itérée de l'opérateur double flèche :

$\begin{matrix} a\uparrow\uparrow\uparrow b= \underbrace{a_{}\uparrow\uparrow a\uparrow\uparrow\dots\uparrow\uparrow a}\\ \qquad\qquad\ \,b\mbox{ exemplaires de }a \end{matrix}$

ainsi que l'opérateur quadruple flèche :

$\begin{matrix} a\uparrow\uparrow\uparrow\uparrow b= \underbrace{a_{}\uparrow\uparrow\uparrow a\uparrow\uparrow\uparrow\dots\uparrow\uparrow\uparrow a}\\ \qquad\qquad\quad b\mbox{ exemplaires de }a \end{matrix}$

et ainsi de suite. La règle générale stipule que l'opérateur n-flèche se développe comme une suite d'opérateurs (n − 1)-flèches. De façon formelle,

$\begin{matrix} a\ \underbrace{\uparrow_{}\uparrow\!\!\dots\!\!\uparrow}\ b= a\ \underbrace{\uparrow\!\!\dots\!\!\uparrow} \ a\ \underbrace{\uparrow_{}\!\!\dots\!\!\uparrow} \ a\ \dots \ a\ \underbrace{\uparrow_{}\!\!\dots\!\!\uparrow} \ a \\ \quad\ \ \,n\qquad\ \ \ \underbrace{\quad n_{}\!-\!\!1\quad\ \,n\!-\!\!1\qquad\quad\ \ \ \,n\!-\!\!1\ \ \ } \\ \qquad\qquad\quad\ \ b\mbox{ exemplaires de }a \end{matrix}$

Définition des puissances itérées

Les puissances itérées de Knuth sont définies formellement de la façon suivante :

$a\uparrow^n b= \left\{ \begin{matrix} a^b\qquad\qquad\qquad\qquad&&\mbox{si }n=1\quad\\ 1\qquad\qquad\qquad\qquad\ &&\mbox{si }b=0\quad\,\\ a\uparrow^{n-1}(a\uparrow^n(b-1))&&\mbox{sinon}\ \, \end{matrix} \right.$

pour tous entiers a, b et n où b ≥ 0 et n ≥ 1.

Cette famille de fonctions peut se définir récursivement par un programme itératif:

function Knuth(rang: naturel;a, b: Naturel) : Naturel
begin
if rang=1
then R=a^b
else begin
    R := 1 (* élément neutre pour l'exponentielle*)
    (* Application b fois de l'opérateur à gauche "a Knuth(rang-1)" *)
    for compteur:=1 to b do R:=Knuth(rang-1,a,R)
    end
return R
end.

Remarques sur la notation

Dans des expressions telles que a^b, la notation pour l'exponentiation est ordinairement d'écrire l'exposant b en exposant au nombre de base a. Mais beaucoup d'environnements, comme les langages de programmation et les e-mails en format de texte brut, ne supportent pas cet agencement bidimensionnel. On a adopté la notation linéaire a↑b pour ces environnements ; la flèche dirigée vers le haut suggère l'élévation à une puissance. Si le jeu de caractère ne contient pas de flèche, l'accent circonflexe ^ est utilisé à la place.

La notation avec exposant a^b ne se prête pas bien à la généralisation, c'est pourquoi Knuth a choisi de travailler à partir de la notation a↑b.

Une autre notation utilisée dans cet article est ↑ⁿ pour indiquer un opérateur flèche d'ordre n.

Tous ces opérateurs (y compris l'exponentiation classique a↑b) sont associatifs à droite, c'est-à-dire que l'évaluation se fait de la droite vers la gauche pour une expression qui contient au moins deux de ces opérateurs. Par exemple, a↑b↑c vaut a↑(b↑c), et non (a↑b)↑c ; autre exemple :

$3\uparrow\uparrow 3=3^{3^3} \mbox{ vaut }3^{(3^3)}=3^{27}=7625597484987 \mbox{ et non } \left(3^3\right)^3=27^3=19683.$

Il existe une bonne raison de choisir ce sens d'évaluation ; en effet, si le choix inverse avait été fait, alors a↑↑b vaudrait a↑(a↑(b-1)), de telle sorte que ↑↑ ne serait pas réellement un opérateur nouveau.

L'associativité à droite est également naturelle puisqu'il est alors possible de réécrire l'expression 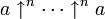$a\uparrow^n\cdots\uparrow^na$ qui apparaît dans le développement de a↑ⁿ⁺¹b comme étant égale à 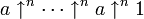$a\uparrow^n\cdots\uparrow^na\uparrow^n1$, de telle sorte que tous les a sont des opérateurs à gauche de l'opérateur flèche. Cela est important puisque les opérateurs flèche ne sont pas commutatifs, et donne l'algorithme pour le calcul itératif de la fonction.

Généralisations

Certains nombres sont si grands que la notation en flèche de Knuth devient trop encombrante pour les décrire. C'est par exemple le cas du nombre de Graham. Les hyper opérateurs ou la flèche chaînée de Conway peuvent alors être utilisées.

$\begin{matrix} a\uparrow^n b&&=&&\mbox{hyper}(a,n+2,b)&&=&&a\to b\to n\\ \mbox{(Knuth)}&&&&&&&&\mbox{(Conway)} \end{matrix}$

On conseille en général l'utilisation de la flèche de Knuth pour les nombres relativement petits, et la flèche chaînée ou les hyper opérateurs pour les plus grands.

Ce document provient de « Notation des puissances it%C3%A9r%C3%A9es de Knuth ».