Moment d'inertie

Pour les articles homonymes, voir Moment.

Lequel de ces mouvements est le plus difficile ?

Le moment d'inertie quantifie la résistance d'un corps soumis à une mise en rotation (ou plus généralement à une accélération angulaire), et a pour grandeur physique M·L² (le produit d'une masse et du carré d'une longueur, qui s'exprime en kg·m² dans le S.I.). C'est l'analogue de la masse inertielle qui, elle, mesure la résistance d'un corps soumis à une accélération linéaire.

Cette appellation est aussi utilisée en mécanique des matériaux pour déterminer la contrainte dans une poutre soumise à flexion. Il s'agit alors d'une notion physique différente, encore appelée moment quadratique, qui a pour grandeur physique L⁴ (la quatrième puissance d'une longueur, exprimée en m⁴ dans le S.I.).

Approche empirique

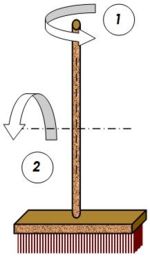
Lorsque l'on prend un balai en main au milieu du manche et qu'on le fait tourner comme sur la figure ci-contre, il est plus aisé de le faire tourner autour de l'axe du manche (1), qu'autour de l'axe transversal indiqué (2).

Cela est dû au fait que dans le deuxième cas, la matière constituant le balai se trouve plus éloignée de l'axe de rotation. Comme pour un solide en rotation, la vitesse linéaire d'un point croît en proportion avec cet éloignement, il est nécessaire de communiquer une plus grande énergie cinétique aux points éloignés. D'où la plus grande résistance du balai à tourner autour d'un axe transversal qu'autour de l'axe du manche.

Détermination du moment d'inertie

Soit un objet physique composé de plusieurs points solidaires i de masse m_i. Cet objet tourne autour d'un axe Δ, à la vitesse angulaire ω. La distance de i à Δ est r_i.

Le calcul de l'énergie cinétique de cet objet donne :

$E_c=\sum_i \tfrac12 m_i V_i^2 = \sum_i \tfrac12 m_i (\omega r_i)^2 = \tfrac12 \omega^2 \sum_i m_i r_i^2$

On définit alors le moment d'inertie J_Δ par rapport à l'axe Δ par :

$J_\Delta=\sum_i m_i r_i^2$

Par extension dans un solide considéré comme un ensemble continu de points matériels x affectés d'une masse volumique ρ, le moment d'inertie s'écrit :

$J_\Delta=\iiint d(x,\Delta)^2\;\mathrm{d}m=\iiint d(x,\Delta)^2\,\rho\;\mathrm {d}V$

où

• d(x,Δ) est la distance entre le point x et l'axe Δ ;
• dV est un volume élémentaire autour de x ;
• dm est la masse de ce volume élémentaire
• ρ est la masse volumique autour de x.

Cette définition peut également prendre une forme vectorielle :

$J_\Delta=\iiint \|\vec\Delta\wedge\vec{OM} \|^2 \mathrm{d}m=\iiint \|\vec\Delta\wedge\vec{OM}\|^2\,\rho\;\mathrm {d}V$

où

• O est un point sur l'axe Δ
• $\vec\Delta$ est un vecteur unitaire de l'axe Δ

Il découle de la définition du moment d'inertie que plus la masse d'un solide est répartie loin de l'axe de rotation, plus son moment d'inertie est important. Ainsi, le patineur sur glace rapproche les bras de son corps lors d'une pirouette. Cela a pour effet de diminuer son moment d'inertie, ce qui, par conservation du moment cinétique, le patineur dépensant autant d'énergie, implique une plus grande vitesse de rotation.

Moments d'inertie particuliers

Pour les exemples suivants, nous considérerons des solides homogène (ρ constant) et de masse M.

La boule

Pour une boule de rayon R et de centre O, les moments d'inertie au centre de la boule par rapport aux trois axes sont égaux :

$\begin{align} 3 J_\Delta &= J_{Ox} + J_{Oy} + J_{Oz} = \int_V [(Oy^2+Oz^2)+(Oz^2+Ox^2)+(Ox^2+Oy^2)]\,\mathrm dm \\ 3 J_\Delta &= 2 \int_V (Ox^2+Oy^2+Oz^2)\,\mathrm dm = 2 \int_O^R r^2 (\rho 4\pi r^2\,\mathrm dr)= \frac{6}{5}M R^2\qquad \text{(avec }M = \rho \frac{4}{3}\pi R^3\text{)} \\ J_\Delta &= \frac{2}{5}M R^2 \end{align}$

Ici, ρ exprime une masse volumique (masse par unité de volume).

La barre

Dans le cas d'une barre de section négligeable et de longueur L, le moment d'inertie selon un axe perpendiculaire à la barre est, en son centre :

$J_\Delta = \int_{-L/2}^{+L/2} x^2\rho\,\mathrm dx = \frac{1}{12} \rho L^3 = \frac{1}{12} M L^2$ (avec M = ρL)

Ici, ρ exprime une masse linéique (masse par unité de longueur).

Le carré

Dans le cas d'un carré de côté a, le moment d'inertie selon un axe perpendiculaire au plan du carré est, en son centre :

$J_\Delta = \int_{-a/2}^{+a/2}\int_{-a/2}^{+a/2} (x^2 + y^2) \rho\,\mathrm dx \mathrm dy = \frac{\rho}{6} a^4 = \frac{M a^2}{6}$ (avec M = ρa²)

Ici, ρ exprime une masse surfacique (masse par unité de surface).

Le cylindre plein

Dans le cas d'un cylindre de rayon R et de hauteur h, le moment d'inertie selon l'axe du cylindre est :

$J_\Delta = \int_{0}^{R} r^2 (\rho 2 \pi r h\,\mathrm dr) = \frac{1}{2} \rho \pi R^4 h = \frac{1}{2} M R^2$ (avec M = ρπR²h)

Ici, ρ exprime une masse volumique (masse par unité de volume).

Le cylindre creux

Dans le cas d'un cylindre creux de rayons intérieur R₁ et extérieur R₂, et de hauteur h, le moment d'inertie selon l'axe du cylindre est :

$J_\Delta = \int_{R_1}^{R_2} r^2 (\rho 2 \pi r h\,\mathrm dr) = 2 \rho \pi h \left[ \frac{r^4}{4} \right]_{R_1}^{R_2} = \frac{1}{2} \rho \pi h (R_2^4 - R_1^4) = \frac{1}{2} M (R_1^2 + R_2^2)$ (avec $M = \rho \pi h (R_2^2 - R_1^2)$)

Ici, ρ exprime une masse volumique (masse par unité de volume).

Théorème de transport (ou théorème d'Huygens ou théorème de Steiner)

Soit l'axe Δ passant par le centre de masse de l'objet, et un axe Δ' parallèle à Δ et distant de d. En calculant comme précédemment le moment d'inertie, on retrouve la relation établie par Christian Huygens connue sous le nom de théorème de transport^[1] ou théorème de Huygens ou théorème de Steiner ou théorème des axes parallèles qui donne le moment d'inertie J_Δ' en fonction de J_Δ  :

$J_{\Delta '}=J_\Delta+M\cdot d^2$

À l'énergie cinétique de rotation propre d'un corps, s'ajoute celle de « translation » circulaire du centre de masse auquel on a affecté la masse totale du solide.

Une conséquence immédiate du théorème de Huygens est qu'il est moins coûteux (en énergie) de faire tourner un corps autour d'un axe passant par le centre de masse.

Voir aussi

Articles connexes

• Moment quadratique
• Matrice d'inertie
• Moment cinétique

Liens externes

Références

1. ↑ Fascicule de L'Université de Liège, Faculté des Sciences Appliquées, Résistance des matériaux et mécanique du solide exercices, 1999, Pro. S. Cescotto (point 3.B.)