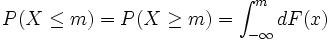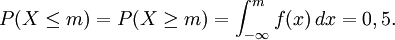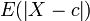- Mediane (centre)
-
Médiane (centre)
En théorie des probabilités et en statistiques, la médiane est un nombre qui divise en deux parties l'échantillon, la population ou la distribution de probabilités tel que chaque partie contient le même nombre de valeurs.
Dans une liste finie de valeurs, il suffit d'ordonner les valeurs dans un ordre croissant et de choisir la valeur centrale comme médiane. S'il y a un nombre pair de valeurs, toute valeur située entre les deux valeurs centrales est acceptable, mais c'est le plus souvent la moyenne arithmétique des deux valeurs centrales qui est utilisée.
Contrairement à la moyenne arithmétique, la valeur médiane permet d'atténuer l'influence perturbatrice des valeurs extrêmes enregistrées lors de circonstances exceptionnelles.
Sommaire
Vulgarisation
Supposons 19 pauvres et un milliardaire dans une pièce. Tous prennent l'argent de leur poche et le déposent sur une table. Chaque pauvre dépose 5 dollars, alors que le milliardaire met 1 milliard de dollars. Le montant total est 1 000 000 095 dollars. Si cet argent est également distribué parmi les vingt personnes, chacune obtient 50 000 004,75 dollars. Ce montant est la valeur moyenne de ce qu'elles ont amené. Cependant, la valeur médiane est de 5 dollars, puisque le groupe peut être divisé en deux parties égales de 10 personnes. On peut donc affirmer que tous les membres du premier groupe ont amené au plus 5 dollars, alors que les membres du deuxième groupe ont amené au moins 5 dollars.
Valeur non-unique
Théoriquement, il peut y avoir plus qu'une valeur médiane: s'il y a un nombre pair de valeurs, il existe différentes valeurs qui divisent l'ensemble en deux parties. Dans ce cas, la moyenne de ces deux valeurs centrales est généralement choisie comme médiane.
Mesure de la dispersion statistique
Lorsque la médiane est utilisée pour situer des valeurs en statistiques descriptives, il existe différentes possibilités pour exprimer la variabilité : L'étendue, l'écart interquartile et l'écart absolu. Puisque la médiane est la même valeur que le deuxième quartile, son calcul est détaillé dans l'article sur les quartiles.
Médianes dans les distributions de probabilités
Pour chacune des distributions de probabilités sur la ligne des nombres réels avec une fonction de distribution cumulative, F, peu importe s'il s'agit d'une distribution continue de probabilités ou d'une distribution discrète de probabilités, une médiane m satisfait l'égalité :
dans laquelle une intégrale de Riemann-Stieltjes apparaît. Pour une distribution de probabilités absolument continue avec une densité de probabilité f, il y a :
Médianes de certaines distributions
Pour toutes les distributions symétriques, la médiane est égale à l'espérance.
- La médiane de la loi normale d'espérance μ et de variance σ2 est μ. Pour cette distribution, espérance = médiane = mode.
- La médiane de la loi uniforme dans l'intervalle [a, b] est (a + b) / 2, qui est aussi l'espérance.
- La médiane de la loi de Cauchy avec le critère de position x0 et le paramètre d'échelle y est x0, le critère de position.
- La médiane de la loi exponentielle avec le facteur d'échelle λ est le facteur d'échelle fois le logarithme naturel de 2, λln 2.
- La médiane de la distribution de Weibull avec le facteur de forme k et le facteur d'échelle λ est λ(log 2)1/k.
Médianes en statistiques descriptives
La médiane est principalement utilisée pour les distributions asymétriques, car elle les représente mieux que la moyenne arithmétique. Considérons l'ensemble { 1, 2, 2, 2, 3, 9 }. La médiane est 2, tout comme le mode, ce qui est une meilleure mesure de tendance centrale que la moyenne arithmétique égale à 3,166….
Le calcul de la médiane est couramment effectué pour représenter différentes distributions et elle est facile à comprendre, tout comme à calculer. Elle est aussi plus robuste que la moyenne en présence de valeurs extrêmes.
Propriétés théoriques
Propriété optimale
La médiane est aussi la valeur centrale qui minimise la valeur moyenne des écarts absolus. Dans la série donnée auparavant, ce serait (1 + 0 + 0 + 0 + 1 + 7) / 6 = 1,5, plutôt que 1,944 à partir de la moyenne. En théorie des probabilités, la valeur c qui minimise
est la médiane de la distribution de probabilités de la variable aléatoire X.
Inégalité impliquant les moyennes et les médianes
Pour les distributions continues de probabilités, la différence entre la médiane et la moyenne est d'au plus d'un écart type.
Calcul efficace
Bien que le tri de n items prend en général O(n log n) opérations, il est possible de calculer la médiane de n items à l'aide de l'algorithme diviser pour régner en seulement O(n) opérations.
Voir aussi
Liens externes
- Portail des probabilités et des statistiques
Catégorie : Statistique descriptive
Wikimedia Foundation. 2010.