- Loi De Darcy
-
Loi de Darcy
La loi expérimentale de Darcy établie par Henry Darcy mesure le débit d'eau qui peut (par gravité et par capillarité) s'écouler à travers un échantillon de milieu poreux, de section A et de longueur L.
Elle décrit le phénomène physique qui est que : plus la couche d'eau est importante, plus celle-ci percole rapidement dans le milieu vers le bas. Elle s'exprime par la formule suivante :
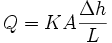
on peut aussi écrire:
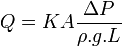
Avec :
ΔP : La différence de pression hydrostatique
Q : Le débit volumique (m3/s).
K : La conductivité hydraulique ou coefficient de perméabilité du milieu poreux (m/s).
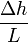 : Le gradient hydraulique (i = Δh/L), ou Δh est la différence des hauteurs piézométriques en amont et en aval de l'échantillon, L est la longueur de l'échantillon.
: Le gradient hydraulique (i = Δh/L), ou Δh est la différence des hauteurs piézométriques en amont et en aval de l'échantillon, L est la longueur de l'échantillon.La conductivité hydraulique K est un coefficient dépendant des propriétés du milieu poreux où l’écoulement a lieu (granulométrie, forme des grains, répartition et forme des pores, porosité intergranulaire) et des propriétés du fluide concerné par les écoulements (la viscosité, le poids spécifique).
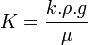
Avec :
k : la perméabilité intrinsèque du milieu poreux (m2).
ρ : la masse volumique du fluide (kg/m3).
g : l'accélération de la pesanteur (m/s2).
μ : la viscosité dynamique du fluide.
Cette loi est valable pour des nombres de Reynolds faibles, sous des conditions stationnaires. En effet, dans ce cas les gradients de pression sont proportionnels aux vitesses d'écoulement pour chacun des pores du milieu poreux (en application de la Loi de Poiseuille). Cette caractéristique demeure lorsqu'on considère un volume relativement large par rapport à la taille des pores, et que l'on considère la moyenne des vitesses d'écoulement et des gradients de pressions de tous les pores dudit volume, ce qui permet d'écrire la Loi de Darcy.
En généralisant à trois dimensions, la loi de Darcy s'écrit
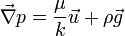
où
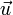 est la vitesse moyenne d'écoulement du fluide,
est la vitesse moyenne d'écoulement du fluide,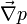 est le gradient de pression aux extrémités du système que l'on considère.
est le gradient de pression aux extrémités du système que l'on considère.Bibliographie et liens
Ouvrages
- Henry Darcy, Les fontaines publiques de la ville de Dijon, V. Dalmont, Paris, (1856)
- GUYON, E., HULIN, J.P., PETIT, L., MITESCU, C.D. Physical hydrodynamics, Oxford University Press, Oxford, (2001)
Voir aussi
Catégories : Hydrogéologie | Mécanique des fluides
Wikimedia Foundation. 2010.

