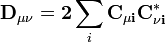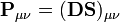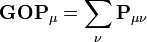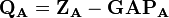- Analyse de population de Mulliken
-
Charge de Mulliken
Les charges de Mulliken proviennent de l' analyse de population de Mulliken et fournissent des moyens d'estimation des charges atomiques partielles à partir des calculs menés au moyen des méthodes de chimie numérique, et en particulier celles basées sur la combinaison linéaire d'orbitales atomiques. Si les coefficients des fonctions de base dans l'orbitale moléculaire sont Cμi pour la μe fonction de base dans la ie orbitale moléculaire, les coefficients de la matrice de densité sont :
pour un système fermé compact dans lequel chaque orbitale moléculaire est doublement occupée. La matrice de population
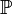 a donc comme coefficients :
a donc comme coefficients :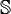 est la matrice de recouvrement des fonctions de base. La somme de l'ensemble des termes de
est la matrice de recouvrement des fonctions de base. La somme de l'ensemble des termes de 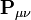 est N - le nombre total d'électrons. L'analyse de population de Mulliken vise à tout d'abord répartire les N électrons sur toutes les fonctions de base. Ceci est fait en prenant les éléments diagonaux de
est N - le nombre total d'électrons. L'analyse de population de Mulliken vise à tout d'abord répartire les N électrons sur toutes les fonctions de base. Ceci est fait en prenant les éléments diagonaux de 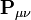 et en factorisant les éléments non-diagonaux de manière égale entre les deux fonctions de base appropriées. Les termes non-diagonaux incluant
et en factorisant les éléments non-diagonaux de manière égale entre les deux fonctions de base appropriées. Les termes non-diagonaux incluant 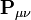 et
et 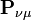 , cela simplifie l'opération à une somme sur une ligne. Cela définit la population orbitalaire brute (en anglais : gross orbital population - GOP) comme :
, cela simplifie l'opération à une somme sur une ligne. Cela définit la population orbitalaire brute (en anglais : gross orbital population - GOP) comme :Les termes
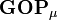 se somment sur N puis répartissent le nombre total d'électrons entre les fonctions de base. Il reste alors à sommer ces termes sur toutes les fonctions de base d'un atome donné A afin d'obtenir la population atomique brute (GAP). L'intégrale des termes
se somment sur N puis répartissent le nombre total d'électrons entre les fonctions de base. Il reste alors à sommer ces termes sur toutes les fonctions de base d'un atome donné A afin d'obtenir la population atomique brute (GAP). L'intégrale des termes 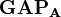 donne aussi N. La charge,
donne aussi N. La charge, 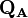 , est ensuite définie comme la différence entre le nombre d'électrons sur l'atome isolé libre, qui est le numéro atomique
, est ensuite définie comme la différence entre le nombre d'électrons sur l'atome isolé libre, qui est le numéro atomique 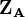 , et la population atomique brute :
, et la population atomique brute :Le problème avec cette approche est la répartition égale des termes non-diagonaux entre les deux fonctions de base. Ceci conduit à des séparations de charges entre les molécules qui sont exagérées. De nombreuses autres méthodes sont utilisées pour déterminer les charges atomiques dans les molécules.
Voir aussi
- Charge partielle
Références
- R. S. Mulliken, J. Chem. Phys.,1955 23, 1833-1840.
- I. G. Csizmadia, Theory and Practice of MO Calculations on Organic Molecules, Elsevier, Amsterdam, 1976.
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Mulliken population analysis ».
- Portail de la chimie
Catégorie : Chimie numérique
Wikimedia Foundation. 2010.