Analyse Harmonique Sur Un Groupe Abélien Fini

Analyse harmonique sur un groupe abélien fini

En mathématiques, l'analyse harmonique sur un groupe abélien fini est un cas particulier d'analyse harmonique correspondant au cas où le groupe est abélien et fini.

L'analyse harmonique permet de définir la notion de transformée de Fourier ou le produit de convolution. Elle est le cadre de nombreux théorèmes comme celui de Plancherel, l'égalité de Parseval ou la dualité de Pontryagin.

Le cas où le groupe est abélien et fini est le plus simple de la théorie, la transformée de Fourier se limite à une somme finie et le groupe dual est isomorphe au groupe d'origine.

L'analyse harmonique sur un groupe abélien fini possède de nombreuses applications, particulièrement en arithmétique modulaire et en théorie de l'information.

Contexte

Algèbre du groupe

Article détaillé : Algèbre d'un groupe fini.

L'analyse harmonique constitue un outil d'étude de l'espace des applications C^G d'un ensemble, ici un groupe abélien fini G (noté dans tout l'article additivement), dans le corps des nombres complexes C. Cet espace dispose de plusieurs structures. Dans un premier temps, comme C est un corps, C^G est un espace vectoriel complexe de dimension g si g désigne l'ordre du groupe G. Il est naturellement muni d'un produit hermitien 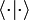$\langle\cdot|\cdot\rangle$ défini par :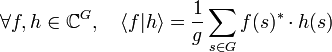

$\forall f,h \in \mathbb C^G,\quad \langle f|h\rangle=\frac 1g \sum_{s \in G} f(s)^*\cdot h(s) \;$

Ici, et dans le reste de l'article si z désigne un nombre complexe, z^* désigne son conjugué. Ce produit hermitien dit canonique, confère à C^G une structure d'espace de Hilbert, noté L²(G).

Dans tout l'article (e_s) où s décrit G, désigne la base canonique de C^G, c'est-à-dire que e_s désigne la fonction qui à t élément de G associe 0 sauf si t est égal à s et alors e_s(s) = 1.

L'espace vectoriel engendré par la famille (e_s) est muni de la multiplication interne suivante, prolongeant celle du groupe G :

$\forall (a_s)_{s\in G} \;, (b_t)_{t\in G}\in \mathbb C^G, \quad \left(\sum_{s\in G} a_s\cdot e_s\right)\cdot\left(\sum_{t\in G} b_t\cdot e_t\right)= \sum_{s,t\in G} a_sb_t\cdot e_{st}\;$

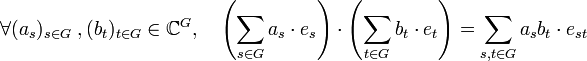
Cette multiplication confère à L²(G) une structure d'algèbre semi-simple, en général notée C[G].

La théorie de l'analyse harmonique sur un groupe abélien fini utilise indifféremment les notations L²(G) ou C[G] pour désigner la structure de base de la théorie. Dans cet article les notations utilisées sont celles de C[G]. Ainsi, si a est un élément de l'algèbre, on utilise ici la notation a_s pour désigner la coordonnée de a dans la base canonique, cette notation correspond à l'égalité a_s = a(s) si a est considéré comme un élément de L²(G).

Groupe dual

Article détaillé : caractère d'un groupe fini.

Le groupe dual de G, noté ici 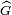$\scriptstyle \widehat G$ est constitué de l'ensemble de s caractères de G. Il forme un groupe isomorphe à G. Il est constitué d'applications de G dans C, donc est inclus dans L²(G) identifié ici à C[G]. Il forme en fait une base orthonormale de l'algèbre.

L'algèbre du groupe dual est canoniquement isomorphe à l'ensemble des applications du groupe dual dans C. Ces applications se prolongent par linéarité en une application qui à une combinaison linéaire de caractère associe un complexe, c'est-à-dire à un élément du dual de l'algèbre C[G]. Le dual de C[G] est donc canoniquement isomorphe à l'algèbre du groupe dual de G.

Théorie de l'analyse harmonique

Transformée de Fourier

Article détaillé : Transformée de Fourier.

L'égalité de Parseval dans le cas d'un espace de dimension finie montre que tout élément a de C[G] vérifie l'égalité suivante :

$a =\sum_{s \in G} a_se_s= \sum_{\chi \in \widehat G} a_{\chi} \chi \quad avec \quad a_{\chi}= <a | \chi>=\frac 1g \sum_{s \in G} a_s^*.\chi(s)\quad et \quad <a|a>= \sum_{\chi \in \widehat G} |a_{\chi}|^2 \;$

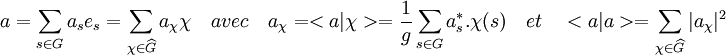
Ici (a_s) désigne les coordonnées de a dans la base canonique et (a_χ) les coordonnées de a dans la base des caractères.

• La transformée de Fourier d'un élément a de C[G] correspond à la fonction généralement notée 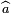$\scriptstyle \widehat a$ du groupe dual de G dans C, c'est à dire une fonction qui à un caractère du groupe associe un complexe, définie par :

$\widehat a(\chi) = \frac{1}{\sqrt g}\sum_{s \in G} a_s\chi(s)^* \;$

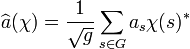
• La transformée de Fourier est une application linéaire de l'algèbre de G dans son dual.

Egalité de Parseval

Article détaillé : Égalité de Parseval.

Le produit hermitien génère une isométrie canonique entre l'algèbre de G et son dual. Il est donc possible de les identifier, dans ce contexte, la propriété suivante est vérifiée :

• La transformée de Fourier sur le groupe G est une isométrie linéaire de l'algèbre du groupe G dans l'algèbre de son dual ce qui se traduit par l'égalité suivante, dite de Parseval :

$\forall a, b \in \mathbb C[G] \quad <a|b>_{\mathbb C[G]} =<\hat a|\hat b>_{\mathbb C[\widehat G]}$

Démonstration

Si b est égal à a, alors comme le groupe dual est une base orthonormale de son algèbre :

$<\hat a|\hat a>_{\mathbb C[\widehat G]}=\frac 1g \sum_{\chi \in \widehat G} \hat a (\chi)^*.\hat a (\chi)= \frac {1}{g^2} \sum_{\chi \in \widehat G} \sum_{s,t \in G} a_s^*\chi(s).a_t\chi(t)^* = \frac {1}{g^2} \sum_{\chi \in \widehat G} \sum_{s \in G} |a_s|^2 = \frac 1g \sum_{s \in G} |a_s|^2 = <a|a>_{\mathbb C[G]} \;$

Enfin, dans le cas général :

$<\hat a + \hat b|\hat a + \hat b> =<\hat a|\hat a> + <\hat b | \hat b> + 2. Reel (<\hat a|\hat b>)\;$ $<a + b|a + b> =< a| a> + < b | b> + 2. Reel (< a| b>)\;$

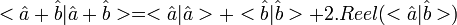
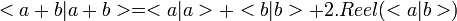
On en déduit :

$Reel (<\hat a |\hat b >) =Reel (<a |b >)\;$

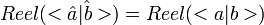
Le même calcul sur <a + b , i(a + b)> montre que les parties imaginaires sont aussi égales. Ce qui démontre le caractère isométrique de la transformation.

L'aspect injectif de la transformation provient du fait qu'elle est une isométrie, la surjectivité se se démontre en remarquant que les deux espaces de départ et d'arrivée ont même dimension.

Formule de Plancherel

Article détaillé : Théorème de Plancherel.

• La formule suivante, dite d'inversion de Plancherel, est vérifiée.

$\forall a \in \mathbb C[G] \quad a = \frac 1{\sqrt g} \sum_{\chi \in \widehat G} \widehat a(\chi) \chi \;$

En effet, les produits hermitiens de chacun des deux membres de l'égalité par un même caractère sont égaux :

$\forall \zeta \in \widehat G \quad <\frac 1{\sqrt g} \sum_{\chi \in \widehat G} \widehat a(\chi) \chi|\zeta> = \frac 1{\sqrt g} \widehat a (\zeta)^* = \frac 1g \sum_{s \in G} a_s^*\zeta(s)=<a|\zeta>$

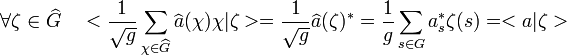
Produit de convolution

Article détaillé : Produit de convolution.

Le produit de convolution se définit simplement dans ce contexte :

• Soit a et b deux éléments de l'algèbre du groupe G ayant pour coordonnées (a_s) et (b_s), le produit de convolution de a et de b, noté a * b, est l'élément de l'algèbre ayant les coordonnées (c_s) définies par :

$c_s=\sum_{t \in G} a_tb_{s-t}\quad donc \quad a*b = \sum_{s \in G} c_s e_s=\sum_{s,t \in G} a_tb_{s-t}e_s \;$

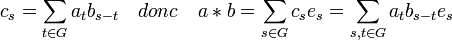
On dispose de la proposition suivante :

• Soit a et b deux éléments de l'algèbre du groupe G, la transformée de Fourier de a * b est le produit des transformées de Fourier de a et de b.

$\forall a,b \in \mathbb C[G] \quad \widehat {a*b} \,(\chi) = \hat a (\chi).\hat b (\chi)\;$

En effet, si χ est un caractère du groupe :

$\widehat {a*b} (\chi) =\frac 1g \sum_{s,t \in G} a_tb_{s-t} \chi(s)^*\;$

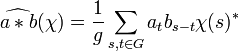
Si l'on note u la valeur s - t, on obtient :

$\widehat {a*b} (\chi) =\frac 1g \sum_{t,u \in G} a_tb_u \chi(t+u)^*= \Big(\frac 1{\sqrt g} \sum_{t \in G} a_t\chi(t)^*\Big).\Big(\frac 1{\sqrt g} \sum_{u \in G} b_u\chi(u)^*\Big) = \hat a (\chi).\hat b (\chi)\;$

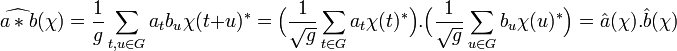
On en déduit les propriétés usuelles du produit de convolution :

• Le produit de convolution est une opération interne de l'algèbre du groupe commutative, associative, distributive par rapport à l'addition.

On peut exprimer ces propriétés de la manière suivante :

• La structure (C[G], + , *) est une algèbre semi-simple isomorphe à l'algèbre du dual de G et donc à C[G].

En effet, il suffit de remarquer que G et son dual sont isomorphes.

Dualité de Pontryagin

Article détaillé : Dualité de Pontryagin.

• Soit H un sous-groupe de G, on appelle groupe orthogonal de H, souvent noté 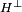$\scriptstyle H^{\perp}$, le sous-groupe du groupe dual de G défini de la manière suivante :

$H^{\perp}= \{ \chi \in \widehat G \quad / \quad \forall h \in H \quad \chi(h) = 1 \}$

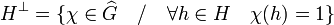
La dualité de Pontryagin s'exprime à travers les trois propriétés suivantes :

• G et son bidual sont canoniquement isomorphes.
• Le dual du quotient G/H est isomorphe à l'orthogonal de H.
• Le dual de H est isomorphe au quotient du dual de G par l'orthogonal de H.

Démonstrations

• G et son bidual sont canoniquement isomorphes.

La démonstration est donnée dans le paragraphe Bidual de l'article caractère d'un groupe fini.

• Le dual du quotient G/H est isomorphe à l'orthogonal de H.

Soit S la surjection canonique de G dans G/H, considérons l'application φ du dual de G/H dans le dual de G définie par :

$\forall s \in G \quad \forall \chi \in \widehat {G/H} \quad \varphi (\chi) (s) = \chi \circ S(s) \;$

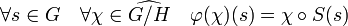
Si χ est un caractère de G/H, alors φ(χ) est la composée de deux morphismes donc est un morphisme et il est à valeur dans C^*, φ(χ) est donc un caractère de G. On remarque de plus que φ est clairement un morphisme de groupe.

Le noyau de S est égal à H, φ possède donc une image incluse dans l'orthogonal de H. Montrons alors que tout élément ζ de l'orthogonal de H possède un antécédent par φ. On remarque que ζ est constant sur toutes les classes de G/H, en effet :

$\forall \bar s \in G/H \quad \forall t \in \bar s \quad \exists h \in H \quad / \quad t = s + h \quad et \quad \zeta(t)=\zeta(s+h) = \zeta(s).\zeta(h)=\zeta(s) \;$

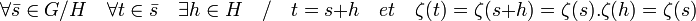
Soit χ le caractère du groupe G/H défini par :

$\forall \bar s \in G/H \quad \chi(\bar s) = \zeta(s) \;$

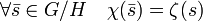
La fonction χ est bien définie car ζ est constant sur toutes les classes de G/H, elle définit bien un morphisme et χ est un caractère de G/H. Son image par φ est clairement égal à ζ. L'application φ possède donc pour image l'orthogonal de H. Son noyau est composé du caractère constant égal à un sur toutes les classes de G/H et l'application φ est donc injective, elle est donc un isomorphisme entre le dual de G/H et le groupe orthogonal de H, ce qui termine la démonstration.

• Le dual de H est isomorphe au quotient du dual de G par l'orthogonal de H.

Soit ψ l'application du dual de G dans le dual de H qui à un caractère du groupe G associe sa restriction à H. L'application ψ est un morphisme de groupe.

Son noyau est composé des caractères constants égaux à 1 sur H, c'est à dire à l'orthogonal de H. Par passage au quotient, on obtient un morphisme θ du quotient du dual de G par l'orthogonal de H à valeur dans le dual de H. La proposition précédente montre l'égalité entre les ordres des ensembles de départ et d'arrivée de θ, et comme θ est injective, la proposition est démontrée.

Formule sommatoire de Poisson

Article détaillé : Formule sommatoire de Poisson.

Dans ce paragraphe H désigne un sous-groupe de G, h son ordre et k l'ordre du groupe orthogonal de H. L'égalité h.k = g est donc vérifiée. On note a un élément de l'algèbre de G et a_s ses coordonnées dans la base canonique.

• L'égalité suivante, dite formule sommatoire de Poisson est vérifiée :

$\frac 1{\sqrt h} \sum_{t \in H} a_t = \frac 1{\sqrt k} \sum_{\chi \in H^{\perp}} \hat a (\chi) \;$

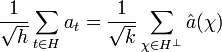Démonstration

Soit b⁰ l'élément de l'algèbre de coordonnées (b_s⁰) dans la base canonique de C[G] définies par les égalités suivantes :

$\forall s \in G \quad b_s^0=\sum_{t \in H} a_{s+t} \quad et \quad b^0 = \sum_{s \in G} b_s^0 e_s\;$

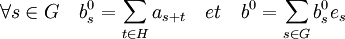
Les coordonnées de b⁰ sont constante sur chaque classe de G/H, ce qui permet de définir un élément b de l'algèbre du groupe G/H dont les coordonnées dans la base canonique indexée par les éléments de G/H sont :

$\forall \bar s \in G/H \quad b_{\bar s} = b_s^0 \;$

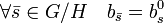
Appliquons alors la formule de Plancherel à l'élément b au point de coordonnées l'élément nul de G/H :

$b_{\bar 0} = \frac 1{\sqrt k} \sum_{\zeta \in \widehat {G/H}} \hat b(\zeta) \zeta(\bar 0) = \frac 1{\sqrt k} \sum_{\zeta \in \widehat {G/H}} \hat b(\zeta) \quad avec \quad \hat b(\zeta) = \frac 1{\sqrt k} \sum_{\bar t \in G/H} b_{\bar t}\zeta(\bar t)^* \;$

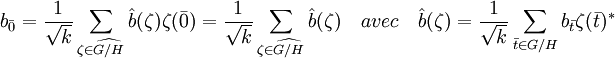
La dualité de Pontryagin montre qu'il existe un unique caractère χ de G tel que si t est un élément de 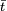$\scriptstyle \bar t$ une classe quelconque de G/H, alors χ(t) est égal à ζ(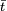$\scriptstyle \bar t$). Soit (u_i) pour i variant de 1 à k une famille de représentants des classes de G/H, les coefficients de Fourier vérifient les égalités suivantes :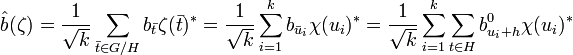

$\hat b(\zeta) = \frac 1{\sqrt k} \sum_{\bar t \in G/H} b_{\bar t}\zeta(\bar t)^* = \frac 1{\sqrt k} \sum_{i=1}^k b_{\bar u_i} \chi(u_i)^* = \frac 1{\sqrt k} \sum_{i=1}^k \sum_{t \in H} b_{u_i + h}^0 \chi(u_i)^*\;$

De plus, le caractère χ est constant sur chaque classe de G/H, on en déduit :

$\hat b(\zeta)=\frac 1{\sqrt k} \sum_{i=1}^k \sum_{t \in H} b_{u_i + h}^0 \chi(u_i + h)^*=\frac 1{\sqrt k} \sum_{s \in G} a_s \chi(s)^* = \sqrt h. \hat a (\chi)\;$

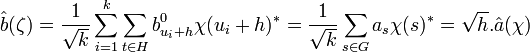
La dualité de Pontryagin indique que si ζ décrit les caractères de G/H, alors χ décrit le groupe orthogonal de H, on en déduit :

$b_{\bar 0} = \frac 1{\sqrt k} \sum_{\zeta \in \widehat {G/H}} \hat b(\zeta) = \sqrt {\frac hk}\sum_{\chi \in h^{\perp}}\hat a (\chi) \;$ $b_{\bar 0} =b_0^0=\sum_{t \in H} a_t = \sqrt {\frac hk}\sum_{\chi \in h^{\perp}}\hat a (\chi) \quad et \quad \frac 1{\sqrt h} \sum_{t \in H} a_t = \frac 1{\sqrt k} \sum_{\chi \in H^{\perp}} \hat a (\chi) \;$

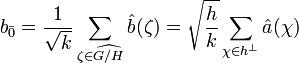
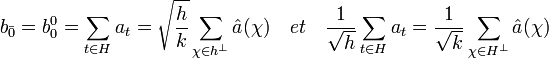
Ce qui termine la démonstration.

Applications

Arithmétique modulaire

Article détaillé : Arithmétique modulaire.

Les premières utilisations historiques des caractères ont pour objectif l'arithmétique. Le symbole de Legendre est un exemple de caractère sur le groupe multiplicatif du corps fini Z/pZ où Z désigne l'anneau des entiers relatifs et p un nombre premier impair.

Il est utilisé pour le calcul des sommes de Gauss ou des périodes de Gauss. Ce caractère est à la base d'une démonstration de la loi de réciprocité quadratique.

Symbole de Legendre

Article détaillé : Symbole de Legendre.

Dans ce paragraphe p désigne un nombre premier impair (c'est-à-dire différent de deux). G est ici le groupe Z/pZ. Le symbole de Legendre désigne la fonction, qui à un entier a, associe 0 si a est un multiple de p, 1 si la classe de a est un carré différent de 0 dans Z/pZ et -1 sinon.

• L'image de la fonction symbole de Legendre sur le groupe multiplicatif de Z/pZ correspond au caractère à valeur dans l'ensemble {-1, 1}.

En effet, le symbole de Legendre est défini sur Z. Cette fonction est constante sur les classes d'entiers modulo p, elle est donc définie sur le groupe multiplicatif de Z/pZ. Sur ce groupe, le symbole de Legendre prend ses valeurs dans l'ensemble {-1, 1} et est un morphisme de groupe, car le symbole de Legendre est un caractère de Dirichlet.

Les démonstrations sont données dans l'article associé.

Somme de Gauss

Article détaillé : Somme de Gauss.

Dans le reste de l'article, F_p désigne le corps fini de cardinal p ou p est un nombre premier impair.

• Soit ψ un caractère du groupe additif (F_p, +) et χ un caractère du groupe multiplicatif (F_p^*, .), alors la somme de Gauss associé à χ et ψ est le nombre complexe, ici noté G(χ, ψ) et défini par :

$G(\chi ,\psi)=\sum_{x \in F_p^*} \chi(x).\psi(x) \;$

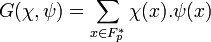
En termes de transformée de Fourier, on peut considérer l'application qui à χ associe G(χ, ψ^*) comme la transformée de Fourier du prolongement de χ à F_p par l'égalité χ(0) = 0 dans le groupe additif du corps et l'application qui à ψ associe G(χ^*, ψ) comme la transformé de Fourier de la restriction de ψ à F_p^* dans le groupe multiplicatif du corps.

Les sommes de Gauss sont largement utilisées en arithmétique, par exemple pour le calcul des périodes de Gauss, elles par exemple, de déterminer la somme des valeurs du groupe des résidus quadratiques des racines p-ièmes de l'unité et plus généralement de déterminer les racines du polynôme cyclotomique d'indice p.

Loi de réciprocité quadratique

Article détaillé : Loi de réciprocité quadratique.

Les sommes de Gauss ont une application historique importante, la loi de réciprocité quadratique, elle s'exprime de la manière suivante :

• Soit p et q deux nombres premiers impairs distincts, l'égalité suivante est vérifiée :

$\left(\frac{p}{q}\right) \left(\frac{q}{p}\right) = (-1)^{\frac{(p-1)(q-1)}{4}}$

Ce théorème est démontré dans l'article Somme de Gauss.

Caractère de Dirichlet

Article détaillé : Caractère de Dirichlet.

Pour démonter le théorème de la progression arithmétique, affirmant que toute classe inversible de l'anneau Z/nZ contient une infinité de nombres premiers, Dirichlet généralise les travaux de Gauss et étudie systématiquement le groupe des caractères du groupe de l'unité d'un quotient de Z.

L'utilisation de la transformée de Fourier est une étape clé de la démonstration. Les caractères de Dirichlet ont un rôle important dans la théorie analytique des nombres particulièrement pour analyser les racines de la fonction ζ de Rieman.

Espace vectoriel fini

Article détaillé : Analyse harmonique sur un espace vectoriel fini.

Un cas particulier est celui des espaces vectoriels sur un corps fini. Les propriétés des corps finis permettent d'établir les résultats de la théorie sous une forme légèrement différente. Ce cas est utilisé par exemple en théorie de l'information à travers l'étude des fonctions booléennes, correspondant au cas où le corps contient deux éléments. La théorie est utilisée pour résoudre des questions de cryptologie notamment pour les boîtes-S, ainsi que pour les chiffrements par flot. L'analyse harmonique sur un espace vectoriel fini intervient aussi dans le contexte de la théorie des codes et particulièrement pour les codes linéaires, par exemple pour établir l'identité de MacWilliams.

Notes et références

Liens externes

• (fr) Dual d'un groupe fini par G. Peyre
• (fr) Analyse harmonique sur les groupes finis commutatifs par A. Bechata
• (fr) Mathématiques discrètes de la transformée de Fourier C. Bachoc Université de Bordeaux I

Références

• Michel Demazure Cours d'algèbre. Primalité, divisibilité, codes Cassini 1997
• Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]
• A. Warusfel Structures algébriques finies Hachette 1971
• G. Peyré L'algèbre discrète de la transformée de Fourier Ellipses Marketing 2004

Ce document provient de « Analyse harmonique sur un groupe ab%C3%A9lien fini ».