- Integrale de chemin
-
Intégrale de chemin
Une intégrale de chemin («path integral» en anglais) est une intégrale fonctionnelle, c'est-à-dire que l'intégrant est une fonctionnelle et que la somme est prise sur des fonctions, et non sur des nombres réels (ou complexes) comme pour les intégrales ordinaires. On a donc ici affaire à une intégrale en dimension infinie. Ainsi, on distinguera soigneusement l'intégrale de chemin (intégrale fonctionnelle) d'une intégrale ordinaire calculée sur un chemin de l'espace physique, que les mathématiciens appellent intégrale curviligne [1].
C'est Richard Feynman qui a introduit les intégrales de chemin en physique dans sa thèse, soutenue en mai 1942, portant sur la formulation de la mécanique quantique basée sur le lagrangien [2]. En raison de la Seconde Guerre mondiale, ces résultats ne seront publiés qu'en 1948 [3]. Cet outil mathématique s'est rapidement imposé en physique théorique avec sa généralisation à la théorie quantique des champs, permettant notamment une quantification des théories de jauge non-abéliennes plus simple que la procédure de quantification canonique.
Par ailleurs, le mathématicien Mark Kac a ensuite développé un concept similaire pour la description théorique du mouvement brownien, s'inspirant de résultats obtenus par Norbert Wiener dans les années 1920. On parle dans ce cas de la formule de Feynman-Kac, qui est une intégrale pour la mesure de Wiener.[4]
Sommaire
Genèse du concept d'intégrale de chemin
Alors qu'il est étudiant de 3e cycle sous la direction de Wheeler à l'université de Princeton, le jeune Feynman cherche une méthode de quantification basée sur le lagrangien pour pouvoir décrire un système ne possédant pas nécessairement d'hamiltonien. Sa motivation première est de quantifier la nouvelle formulation de l'électrodynamique classique basée sur l'action à distance qu'il vient juste de développer avec Wheeler[5].
Au printemps de 1941, il rencontre Herbert Jehle, alors visiteur à Princeton, qui lui indique lors d'une soirée à la Nassau Tavern l'existence d'un article de Dirac qui discute précisément la quantification à partir du lagrangien [6]. Jehle précise à Feynman que cette formulation permet une approche relativiste covariante bien plus aisée que celle basée sur le hamiltonien. Le lendemain, les deux physiciens se rendent à la bibliothèque pour étudier l'article de Dirac. Ils y lisent notamment la phrase suivante : pour deux instants
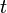 et
et 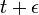 voisins, l'amplitude de transition élémentaire :
voisins, l'amplitude de transition élémentaire :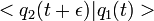 est analogue à
est analogue à ![\exp ( i S[q]/\hbar )\,](/pictures/frwiki/102/f0f0ac1206095833ebdf16daf0b0873c.png)
Dans cette formule, la grandeur
![S[q(t)]\,](/pictures/frwiki/48/0e9fd62e69c48d17f5295b0c4d75f7a8.png) est l'action classique :
est l'action classique :![S[q_2(t + \epsilon) ,q_1(t)] \ = \ \int_{t}^{t + \epsilon} L(q,\dot{q}) \ dt \ = \ L \left( q_1, \frac{q_2-q_1}{\epsilon} \right) \ \epsilon\,](/pictures/frwiki/102/ffe056acc92b67324e8f86305088fa1b.png)
Afin de comprendre ce que Dirac veux dire par analogue, Feynman étudie le cas d'une particule non relativiste de masse
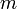 pour laquelle le lagrangien s'écrit :
pour laquelle le lagrangien s'écrit :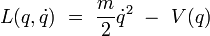
On sait que :
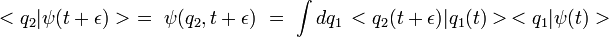
Feynman suppose alors une relation de proportionnalité :
![\psi(q_2,t + \epsilon) \ = \ A \ \int dq_1 \, \exp \, \left( \, i \, \frac{S[q(t)]}{\hbar} \, \right) \ \psi(q_1,t)](/pictures/frwiki/55/70f482eccc0090e48a8ac8cb398a1cc1.png)
où
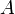 est une constante inconnue. En présence de Jehle, Feynman démontre que cette équation implique que
est une constante inconnue. En présence de Jehle, Feynman démontre que cette équation implique que 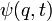 obéit à l'équation de Schrödinger :
obéit à l'équation de Schrödinger :![\left[ \, - \ \frac{\hbar^2}{2m} \ \frac{\partial^2 ~~}{\partial q^2} \ + \ V(q) \, \right] \ \psi(q,t) \ = \ i \, \hbar \ \frac{\partial ~~}{\partial t}\psi(q,t)](/pictures/frwiki/57/94bb8fbd11b93cd266a0f0eb81ceefd8.png)
à la condition que la constante inconnue A soit égale à :
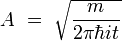
À l'automne 1946, lors du bicentenaire de l'université de Princeton, Feynman rencontra Dirac et le bref échange suivant eut lieu:
- - Feynman : « Saviez-vous que ces deux grandeurs étaient proportionnelles ? »
- - Dirac : « Elles le sont ? »
- - Feynman : « Oui. »
- - Dirac : « Oh ! C'est intéressant. »
Cette réponse laconique mettra un point final à la discussion ... Pour plus de détails historiques, on lira avec profit l'article de Schweber [7].
Rappels sur le propagateur de l'équation de Schrödinger
Pour simplifier les notations, on se restreint ci-dessous au cas d'une seule dimension d'espace. Les résultats s'étendent sans difficulté à un nombre quelconque de dimensions.
Définition
Considérons une particule de masse
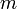 non relativiste, décrite en mécanique quantique par une fonction d'onde. Supposons que l'on se donne la condition initiale
non relativiste, décrite en mécanique quantique par une fonction d'onde. Supposons que l'on se donne la condition initiale 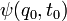 à un instant initial
à un instant initial 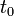 fixé. Alors, la fonction d'onde à un instant ultérieur
fixé. Alors, la fonction d'onde à un instant ultérieur 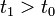 , solution de l'équation de Schrödinger, est donnée par l'équation intégrale :
, solution de l'équation de Schrödinger, est donnée par l'équation intégrale :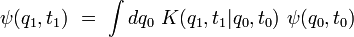
où
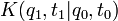 est le propagateur de la particule :
est le propagateur de la particule :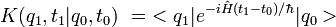
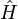 est l'opérateur hamiltonien de la particule.
est l'opérateur hamiltonien de la particule.Equation de Chapman-Kolmogorov
Rappelons que, si
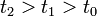 , le propagateur obéit à l'équation de Chapman-Kolmogorov :
, le propagateur obéit à l'équation de Chapman-Kolmogorov :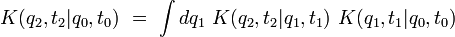
Cette relation va nous permettre de trouver l'expression du propagateur en termes d'une intégrale de chemin.
Expression du propagateur en termes d'intégrale de chemin
Cherchons l'expression du propagateur
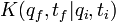 entre l'instant initial
entre l'instant initial 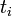 et l'instant final
et l'instant final 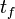 .
.Application de l'équation de Chapman-Kolmogorov
On découpe l'intervalle de temps
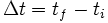 en
en 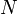 intervalles de temps élémentaires de durée
intervalles de temps élémentaires de durée  en introduisant les
en introduisant les 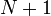 instants :
instants :
avec
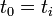 et
et 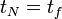 . Il y a donc
. Il y a donc 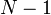 instants intermédiaires
instants intermédiaires 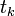 entre l'instant initial
entre l'instant initial 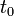 et l'instant final
et l'instant final 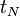 . Pour que les intervalles de temps aient une durée
. Pour que les intervalles de temps aient une durée 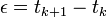 élémentaire, la limite
élémentaire, la limite 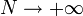 est sous-entendue.
est sous-entendue.L'application de l'équation de Chapman-Kolmogorov une première fois permet d'écrire :
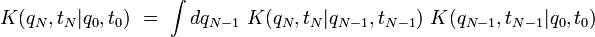
puis, en l'appliquant une deuxième fois :
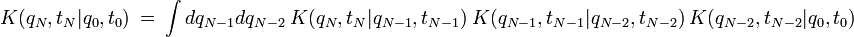
et ainsi de suite. On obtient au final après
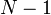 applications aux
applications aux 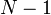 temps intermédiaires[8] :
temps intermédiaires[8] :![K(q_N,t_N|q_0,t_0) \ = \ \int \left[ \, \prod_{k=1}^{N-1} dq_k \, \right] \ K(q_N,t_N|q_{N-1},t_{N-1}) \times \dots \times K(q_{k+1},t_{k+1}|q_{k},t_{k}) \times \dots \times K(q_{1},t_{1}|q_0,t_0)](/pictures/frwiki/100/d525ac09f5944c10cacd8c1969dc1628.png)
On est ainsi amené à considérer le propagateur élémentaire :
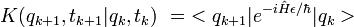
Propagateur élémentaire : formule de Feynman-Dirac
Pour une particule de masse
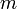 non relativiste à une dimension dans un potentiel, dont l'opérateur Hamiltonien s'écrit :
non relativiste à une dimension dans un potentiel, dont l'opérateur Hamiltonien s'écrit :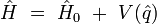
et le propagateur élémentaire s'écrit :
![K(q_{k+1},t_{k+1}|q_{k},t_{k}) \ = \ < q_{k+1} |e^{-i \, [ \, \hat{H}_0 + V(\hat{q}) \, ] \, \epsilon /\hbar} | q_k >](/pictures/frwiki/55/79913cbea2dd47ca49c3d2bf6a19afd6.png)
On utilise la formule de Trotter-Kato :
![e^{t(\hat{A} + \hat{B})} \ = \ \lim_{n \to \infty} \ \left[ \ e^{\hat{A}t/n} \ \times \ e^{\hat{B}t/n} \ \right]^n](/pictures/frwiki/54/6a7af09d6c118d00474c31ca24a8276d.png)
Cette formule n'est pas triviale, car les opérateurs
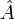 et
et 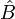 ne commutent en général pas ! On obtient ici :
ne commutent en général pas ! On obtient ici :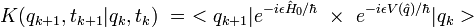
On peut sortir l'exponentielle contenant le potentiel qui ne dépend que de la position :
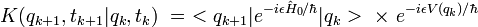
L'élément de matrice restant est le propagateur de la particule libre, donc on peut finalement écrire l'expression :
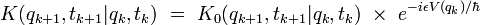
Or l'expression du propagateur libre est connue exactement :
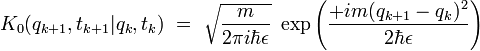
On remarque que l'argument de l'exponentielle peut se réécrire en termes d'une expression discrètisée de la vitesse :
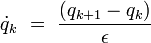
comme :
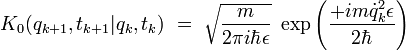
On en déduit que le propagateur élémentaire s'écrit :
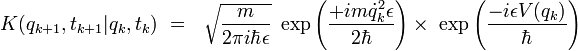
Les arguments des deux exponentielles étant maintenant des nombres complexes, on peut écrire sans difficultés :
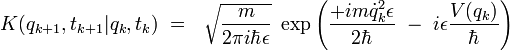
soit encore :
![K(q_{k+1},t_{k+1}|q_{k},t_{k}) \ = \ \ \sqrt{\frac{m}{2 \pi i \hbar \epsilon}} \ \exp \left[ + \frac{i}{\hbar} \ \left( \frac{m}{2} \dot{q}_k^2 \ - \ V(q_k) \right) \ \epsilon \ \right]](/pictures/frwiki/100/d2e6c64d9a6b0993d7984a6756c4d2a8.png)
Le terme entre parenthèse représente le Lagrangien de la particule :
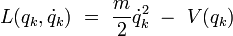
d'où la formule de Feynman-Dirac pour le propagateur élémentaire :
![K(q_{k+1},t_{k+1}|q_{k},t_{k}) \ = \ \ \sqrt{\frac{m}{2 \pi i \hbar \epsilon}} \ \exp \left[ + \frac{i}{\hbar} \ L(q_k,\dot{q}_k) \ \epsilon \ \right]](/pictures/frwiki/52/4dac735213dbe66e97e99cd56ce05dee.png)
Intégrale de chemin
On injecte l'expression de Feynman-Dirac dans la formule générale :
![K(q_N,t_N|q_0,t_0) \ = \ \int \left[ \, \prod_{k=1}^{N-1} dq_k \, \right] \ K(q_N,t_N|q_{N-1},t_{N-1}) \times \dots \times K(q_{k+1},t_{k+1}|q_{k},t_{k}) \times \dots \times K(q_{1},t_{1}|q_0,t_0)](/pictures/frwiki/100/d525ac09f5944c10cacd8c1969dc1628.png)
Il vient :
![K(q_N,t_N|q_0,t_0) \ = \ \left( \, \frac{m}{2 \pi i \hbar \epsilon} \, \right)^{N/2} \ \int \left[ \, \prod_{k=1}^{N-1} dq_k \, \right] \ \exp \left[ + \frac{i}{\hbar} \ L(q_{N-1},\dot{q}_{N-1}) \ \epsilon \ \right] \times \dots \times \exp \left[ + \frac{i}{\hbar} \ L(q_k,\dot{q}_k) \ \epsilon \ \right] \times \dots \times \exp \left[ + \frac{i}{\hbar} \ L(q_0,\dot{q}_0) \ \epsilon \ \right]](/pictures/frwiki/49/1958e35f000c6df83210aedf460d91a7.png)
L'argument des exponentielles étant des nombres complexes, on peut écrire :
![K(q_N,t_N|q_0,t_0) \ = \ \left( \, \frac{m}{2 \pi i \hbar \epsilon} \, \right)^{N/2} \ \int \left[ \, \prod_{k=1}^{N-1} dq_k \, \right] \ \exp \left[ + \frac{i}{\hbar} \ \left[ \, L(q_{N-1},\dot{q}_{N-1}) + \dots + L(q_k,\dot{q}_k) + \dots + L(q_0,\dot{q}_0) \, \right] \ \epsilon \ \right]](/pictures/frwiki/54/63a8e31f7a4b036d75d0d1387c09b498.png)
On reconnait dans l'argument de l'exponentielle une discrétisation de l'action classique :
![\lim_{N\to\infty} \sum_{k=1}^{N-1} L(q_k,\dot{q}_k) \epsilon \ = \ \int_{t_0}^{t_N} L(q(t),\dot{q}(t)) dt \ = \ S \left[ \, q(t) \, \right]](/pictures/frwiki/102/f9528674af5aeaf41cbd5441eb7d1203.png)
On en déduit avec Feynman l'expression du propagateur comme intégrale fonctionnelle sur tous les chemins continus :
![K(q_N,t_N|q_0,t_0) \ = \ \int \mathcal{D}q(t) \ \textrm{e}^{ + \frac{i \, S \left[ \, q(t) \, \right]}{\hbar}}](/pictures/frwiki/49/11de894d712ef0667ca37000ce0e709c.png)
avec la mesure formelle[9] :
![\mathcal{D}q(t) \ = \ \lim_{N\to\infty} \left( \, \frac{m}{2 \pi i \hbar \epsilon} \, \right)^{N/2} \ \left[ \, \prod_{k=1}^{N-1} dq_k \, \right]](/pictures/frwiki/52/4673b2ac26a7fc1248cb2842e76d3746.png)
Interprétation
La formule de Feynman :
![K(q_f,t_f|q_i,t_i) \ = \ \int \mathcal{D}q(t) \ \textrm{e}^{ + \frac{i \, S \left[ \, q(t) \, \right]}{\hbar}}](/pictures/frwiki/99/c44fe6f004a074e716d66ac3cf21b97c.png)
admet l'interprétation suivante : pour calculer l'amplitude de transition du point initial
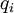 à l'instant
à l'instant 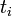 vers le point final
vers le point final 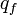 à l'instant tf, il faut considèrer tous les chemins continus[10]
à l'instant tf, il faut considèrer tous les chemins continus[10] 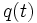 vérifiants les conditions aux limites :
vérifiants les conditions aux limites : 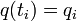 et
et 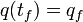 . Chaque chemin se voit attribuer un « poids » complexe de module unité :
. Chaque chemin se voit attribuer un « poids » complexe de module unité : ![\exp ( i S[q(t)]/\hbar )\,](/pictures/frwiki/100/dd1e01dee08cad29a0c1208abd9811ed.png) , où
, où ![S[q(t)]\,](/pictures/frwiki/48/0e9fd62e69c48d17f5295b0c4d75f7a8.png) est l'action classique calculée sur ce chemin. On « somme » alors cette infinité non dénombrable de poids complexes, et on obtient in fine l'amplitude de transition désirée.
est l'action classique calculée sur ce chemin. On « somme » alors cette infinité non dénombrable de poids complexes, et on obtient in fine l'amplitude de transition désirée.Cette interprétation est l'œuvre de Feynman seul, Dirac n'ayant pas franchi le pas. Elle est implicite dans sa thèse de 1942, et explicite dans la publication de 1948.
Limite semi-classique
Dans la limite où l'action du système est beaucoup plus grande que
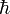 , on peut utiliser un développement du type semi classique, où y est une petite perturbation de la trajectoire classique xc: x = xc + y
, on peut utiliser un développement du type semi classique, où y est une petite perturbation de la trajectoire classique xc: x = xc + yConsidérons un Lagrangien standard:
![\mathcal{L}[x,\dot{x}]= \frac{m\dot{x}^{2}}{2}- V(x)](/pictures/frwiki/97/aabc30b9b9f82daf69db73f1f376c7c4.png)
On écrit alors l'action sous la forme suivante, en se limitant au deuxième ordre:
![S[x] \approx S[x_{c}]+ \int_{t_{i}}^{t_{f}}dt \underbrace{\frac{\delta S}{\delta x(t)}|_{x_{c}}}_{=0} y(t) + \frac{1}{2} \int_{t_{i}}^{t_{f}}dt_{1} dt_{2} \frac{\delta^{2} S}{\delta x(t_{1})\delta x(t_{2}) }|_{x_{c}}y(t_{1})y(t_{2})\Longrightarrow](/pictures/frwiki/97/a2af42c15acf496b8eb59cbf9e0fcc11.png)
![S[x]\approx S[x_{c}]+ \frac{1}{2} \int_{t_{i}}^{t_{f}}dt (m \dot{y}^{2} - V''(x_{c}) y^{2})](/pictures/frwiki/51/31659c3c8a96ea1bff7209fd7974bdb8.png)
on peut donc approximer le propagateur:
![K(x_{f},t_{f};x_{i},t_{i}) \approx e^{i S[x_{c}]/ \hbar} \int \mathcal{D}[y] e^{i \int_{t_{i}}^{t_{f}}dt (m \dot{y}^{2} - V''(x_{c}) y^{2})/2\hbar}](/pictures/frwiki/51/34a01a003d70ba5737366c55bdc21769.png)
une intégration par partie de l'exposant ramène à une forme Gaussienne:
![K(x_{f},t_{f};x_{i},t_{i})\approx e^{i S[x_{c}]/ \hbar} \int \mathcal{D}[y] e^{i \int_{t_{i}}^{t_{f}}dt (y[-m \frac{d^{2}}{dt^{2}} - V''(x_{c}] y)/2\hbar}](/pictures/frwiki/50/2922ad0fcf82f997d7c301df4ff54768.png)
Définissons l'opérateur
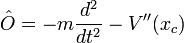
les règles de calcul des intégrales Gaussiennes fournissent:
![K(x_{f},t_{f};x_{i},t_{i}) \approx cste \cdot \sqrt{\frac{1}{Det (\hat{O})}}\cdot e^{i S[x_{c}]/ \hbar}](/pictures/frwiki/54/670ad65fe69c000b2c03ba8e2ee198cf.png)
Considérons maintenant la fonction Ψ(t) définie comme suit:
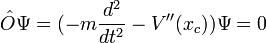
avec les conditions de bords:
Ψ(ti) = 0
Ψ'(ti) = 1
On peut alors montrer que:
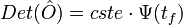
ce qui nous donne pour l'approximation du propagateur:
![K(x_{f},t_{f};x_{i},t_{i}) \approx \sqrt{\frac{A}{\Psi(t_{f})}}\cdot e^{i S[x_{c}]/ \hbar}](/pictures/frwiki/99/cf282603976ee6a16a78d82e308ab3ce.png)
on détermine la constante A à partir du propagateur de la particule libre:
![K_{fp}(x_{f},t_{f};x_{i},t_{i})=\sqrt{\frac{m}{2\pi i \hbar (t_{f}-t_{i})}} e^{i S[x_{c}]/ \hbar}](/pictures/frwiki/53/58aedadc4a116db583b15d5e1960c58f.png)
dans le cas de la particule libre, la fonction Ψ qui satisfait les conditions exposées plus haut est Ψ(t) = t − ti, ce qui nous donne immédiatement une expression pour A. On obtient finalement l'approximation dite semi-classique du propagateur:
![K(x_{f},t_{f};x_{i},t_{i}) \approx \sqrt{\frac{m}{2 \pi i \hbar \Psi(t_{f})}}\cdot e^{i S[x_{c}]/ \hbar}](/pictures/frwiki/97/a400c660a68b8b9d59da52c147c417f3.png)
cette approximation est puissante, et peut même donner parfois un résultat exact, comme par exemple dans le cas où le potentiel est celui d'un oscillateur harmonique de fréquence ω. Dans ce cas, la fonction Ψ doit satisfaire, en plus des conditions de bord:
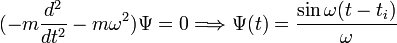
et on obtient l'expression exacte du propagateur de l'oscillateur harmonique, par l'approximation semi-classique:
![K_{ho}(x_{f},t_{f};x_{i},t_{i}) = \sqrt{\frac{m \omega}{2 \pi i \hbar \sin \omega(t_{f}-t_{i})}}\cdot e^{i S[x_{c}]/ \hbar}](/pictures/frwiki/50/2ab2a18072011a587efc8f885ee46092.png)
avec l'action classique de l'oscillateur harmonique:
![S_{cl}[x]= \int_{t_{i}}^{t_{f}} dt \mathcal{L}[x,\dot{x}] = \frac{m\omega}{2}\left[(x_{f}^{2}+x_{i}^{2})\cot\omega (t_{f}-t_{i})-\frac{2x_{i}x_{f}}{\sin\omega (t_{f}-t_{i})}\right]](/pictures/frwiki/48/08fa3dfef8fd286276232bc536be0a08.png)
à noter une autre formulation équivalente de l'approximation semi-classique, dite de Van Vleck-Pauli-Morette, qui découle directement de la précédente:
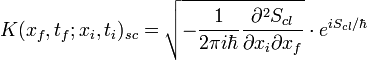
Bibliographie
Textes historiques
- Richard P. Feynman ; The principle of least action in quantum mechanics, thèse de l'université de Princeton. Cette thèse vient d'être publiée par Laurie M. Brown (cf. ci-dessous).
- Richard P. Feynman ; Space-time approach to non-relativistic quantum mechanics, Review of Modern Physics 20 (1948) 267. Cet article est reproduit dans : Julian Schwinger (ed) ; Selected papers on quantum electrodynamics, Dover Publications, Inc. (1958) (ISBN 0-486-60444-6).
- PAM Dirac ; The lagrangian in quantum mechanics, Physikalische Zeitschrift der Sowjetunion 3(1) (1932) 64. Cet article est reproduit dans : Julian Schwinger (ed) ; Selected papers on quantum electrodynamics, Dover Publications, Inc. (1958) (ISBN 0-486-60444-6).
- Laurie M. Brown (Editor) ; Feynman's thesis: a new approach to quantum theory, World Scientific (2005),(ISBN 981-256-380-6). Contient la thèse originale de Feynman, ainsi que les deux articles précédents.
Ouvrages de références
- Jean Zinn-Justin ; Intégrale de chemin en mécanique quantique : Introduction, Collection savoirs actuels, E.D.P. Sciences/C.N.R.S. Editions (2003), (ISBN 2-86883-660-7). Excellente introduction au sujet, ce livre est le fruit de nombreuses années d'enseignement au Magistère Interuniversiataire de Physique de l'E.N.S.
- Claude Cohen-Tannoudji ; Compléments de mécanique quantique, (1966). Cours donné en 1966 par le prix Nobel 1997 (Collège de France, Paris). Aborde la formulation Lagrangienne de la mécanique quantique, et l'utilisation des fonctions de Green. Notes de cours rédigées en 1966 par Serge Haroche (Collège de France, Paris).
- Richard P. Feynman and André R. Hibbs, Quantum Mechanics and Path Integrals, New York: McGraw-Hill (1965), (ISBN 0-07-020650-3).
- Larry S. Schulman ; Techniques & Applications of Path Integration, Jonh Wiley & Sons (New York-1981), ISBN . Réédité par Dover Publications, Inc. (2005), (ISBN 0-486-44528-3). Une autre référence, un peu plus moderne que la précédente.
- Christian Grosche & Frank Steiner; Handbook of Feynman Path Integrals, Springer Tracts in Modern Physics 145, Springer-Verlag (1998), (ISBN 3-540-57135-3).
- Philippe A. Martin ; L'intégrale fonctionnelle ; Presses Polytechniques Universitaires Romandes (1996), (ISBN 2-88074-331-1).
- Lundqvist & co ; Path Summation ; World scientific (1988), (ISBN 9971-5-0597-5).
- Martin Veltman ; Diagrammatica, CambridgeLNP
- Lewis H. Ryder ; Quantum Field Theory (Cambridge University Press, 1985), (ISBN 0-521-33859-X).
- R.J. Rivers ; Path Integrals Methods in Quantum Field Theory, Cambridge University Press (1987), (ISBN 0-521-25979-7).
- Hagen Kleinert, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore, 2004), (ISBN 981-238-107-4). (Disponible aussi en ligne au format pdf).
- Christian Grosche ; An introduction into the Feynman path integral, cours donné au Quantenfeldtheorie und deren Anwendung in der Elementarteilchen- und Festkörperphysik, Universität Leipzig, 16-26 November 1992. Texte complet disponible sur l'ArXiv : hep-th/9302097.
- Sanjeev Seahra ; Path Integrals in Quantum Field Theory, notes du cours Quantum Field Theory donné en 2000 par Eric Poisson à l'University of Waterloo (Canada). Texte complet disponible au format pdf.
- Richard MacKenzie ; Path integral methods and applications, cours donné aux Rencontres du Vietnam: VIth Vietnam School of Physics, Vung Tau, Vietnam, 27 December 1999 - 8 January 2000. Texte complet disponible sur l'ArXiv : quant-ph/0004090.
- Gert Roepstorff ; Path Integral Approach to Quantum Physics, Springer-Verlag (1994), (ISBN 3-540-55213-8).
Approche mathématiquement rigoureuse
- S. Albeverio & R. Hoegh-Krohn. ; Mathematical Theory of Feynman Path Integral, Lecture Notes in Mathematics 523, Springer-Verlag (1976), ISBN .
- James Glimm et Arthur Jaffe Quantum Physics: a Functional Integral Point of View, New York: Springer-Verlag (1981), (ISBN 0-387-90562-6).
- Gerald W. Johnson and Michel L. Lapidus ; The Feynman Integral and Feynman's Operational Calculus, Oxford Mathematical Monographs, Oxford University Press (2002), (ISBN 0-19-851572-3).
- Etingof, Pavel ; Geometry and Quantum Field Theory, M.I.T. OpenCourseWare (2002). Ce cours en ligne, conçu pour les mathématiciens, est une introduction rigoureuse à la théorie quantique des champs via les intégrales fonctionnelles.
- Cécile DeWitt-Morette ; Feynman's path integral - Definition without limiting procedure, Communication in Mathematical Physics 28(1) (1972) pp. 47–67. Texte complet disponible sur : Euclide Project.
- Pierre Cartier & Cécile DeWitt-Morette ; A new perspective on functional integration, Journal of Mathematical Physics 36 (1995) pp. 2137-2340. Texte complet disponible sur l'ArXiv : funct-an/9602005.
- Pierre Cartier ; L'intégrale de chemin de Feynman : d'une vue intuitive à un cadre rigoureux, dans : Leçons de mathématiques d'aujourd'hui, Collection Le sel et le fer, Cassini (2000) pp.27-59 (ISBN 2-84225-007-9).
- Alain Connes & Dirk Kreimer : Communication in Mathematical Physics 210 (2000)1. 249-273
- Alain Connes & Marcolli : Communication in Mathematical Physics 216 (2001),1, 215-241
- Alain Connes ; page personnelle, articles 137, 148, 155, 157, 158, 162, 165, 167.
Notes et références
- ↑ Les physiciens qualifient l'intégrale curviligne d'un champ de vecteur de circulation (par exemple, le travail d'une force.)
- ↑ Richard P. Feynman ; The principle of least action in quantum mechanics, thèse de l'université de Princeton. Cette thèse vient d'être publiée dans Laurie M. Brown (Editor) ; Feynman's thesis: a new approach to quantum theory, World Scientific (2005),(ISBN 981-256-380-6).
- ↑ Richard P. Feynman ; Space-time approach to non-relativistic quantum mechanics, Review of Modern Physics 20 (1948) 267. Cet article est reproduit dans : Julian Schwinger (ed) ; Selected papers on quantum electrodynamics, Dover Publications, Inc. (1958) (ISBN 0-486-60444-6), ainsi que dans : Laurie M. Brown (Editor) ; Feynman's thesis: a new approach to quantum theory, World Scientific (2005),(ISBN 981-256-380-6).
- ↑ Il existe clairement un lien formel entre les deux types d'intégrales de chemins - Feynman et Wiener -, car alors que l'équation de Schrödinger d'une particule massive non relativiste libre s'écrit :
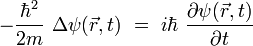 où ψ est la fonction d'onde quantique, l'équation de la diffusion dans l'espace pour la densité de probabilité P s'écrit :
où ψ est la fonction d'onde quantique, l'équation de la diffusion dans l'espace pour la densité de probabilité P s'écrit : 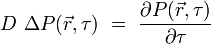 On voit clairement qu'il suffit de poser :
On voit clairement qu'il suffit de poser : 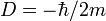 pour le coefficient de diffusion, et : t = iτ pour le temps pour transformer l'équation de Schrödinger en équation de la diffusion. Or, il se trouve que l'intégrale de chemin de Wiener - pour l'équation de la diffusion - est plus facile à définir mathématiquement rigoureusement que celle de Feynman - pour l'équation de Schrödinger. Certains auteurs ont donc proposé de définir l'intégrale de Feynman à partir de la mesure de Wiener en faisant un prolongement analytique pour les temps imaginaires.
pour le coefficient de diffusion, et : t = iτ pour le temps pour transformer l'équation de Schrödinger en équation de la diffusion. Or, il se trouve que l'intégrale de chemin de Wiener - pour l'équation de la diffusion - est plus facile à définir mathématiquement rigoureusement que celle de Feynman - pour l'équation de Schrödinger. Certains auteurs ont donc proposé de définir l'intégrale de Feynman à partir de la mesure de Wiener en faisant un prolongement analytique pour les temps imaginaires. - ↑ Cette théorie ne sera publiée qu'en 1945 : John Archibald Wheeler & Richard P. Feynman ; Review of Modern Physics 17 (1945) 157.
- ↑ PAM Dirac ; The lagrangian in quantum mechanics, Physikalische Zeitschrift der Sowjetunion 3(1) (1932) 64. Cet article est reproduit dans : Julian Schwinger (ed) ; Selected papers on quantum electrodynamics, Dover Publications, Inc. (1958) (ISBN 0-486-60444-6), ainsi que dans : Laurie M. Brown (Editor) ; Feynman's thesis: a new approach to quantum theory, World Scientific (2005),(ISBN 981-256-380-6).
- ↑ Silvian S. Schweber ; Feynman's visualization of space-time processes, Review of Modern Physics 58(2) (1986) 449-508.
- ↑ Cette équation avait été écrite par Dirac dans son article de 1933.
- ↑ Un gros problème dans cette définition est que cette "mesure formelle" n'est pas une vraie mesure au sens rigoureux du mathématicien. Pour une définition rigoureuse de l'intégrale de Feynman, consulter les traités - souvent très techniques - de la bibliographie.
- ↑ L'analogie avec le mouvement Brownien montre que les chemins qui contribuent de façon significative à l'intégrale de Feynman sont continus, mais non différentiables. Plus précisément, ce sont des chemins Lipchitziens d'exposants 1/2.
- Portail de la physique
Catégories : Physique théorique | Théorie de l'intégration | Probabilités
Wikimedia Foundation. 2010.
