Algèbre des fonctions

Fonction (mathématiques élémentaires)

Pour les articles homonymes, voir Fonction.

Cet article fait partie de la série Mathématiques élémentaires

Algèbre

Logique

Arithmétique

Probabilités

Statistiques

En mathématiques élémentaires, plus de 90 % des fonctions rencontrées sont des fonctions numériques, mais la notion de fonction ne se limite pas à celle-ci .

• L'article qui suit présente quelques règles à connaître sur les fonctions
• L'article fonction numérique traite des fonctions numériques en mathématiques élémentaires
• L'article fonction (mathématiques) les présente dans leur généralité.

Les fonctions

Les fonctions sont des outils. Pour être une fonction il faut respecter des règles scrupuleuses. Elles ont de nombreuses propriétés. Nous présentons ici les bases .

Les règles scrupuleuses

• Avoir un ensemble de départ contenant l'ensemble de définition de la fonction et un ensemble d'arrivée.

• À chaque élément de cet ensemble de définition faire correspondre un de ceux de l'ensemble d'arrivée.

En mathématiques élémentaires, la première de ces règles (pourtant primordiale) est souvent oubliée par les élèves car les exemples qui sont proposés se limitent à quelques ensembles de départ et d'arrivée naturels dans le contexte de travail (ensemble des réels pour les fonctions numériques, ensemble des points du plan pour les fonctions ponctuelles)

Toutefois elle reste importante.

Image, antécédent

Si à un élément a, on fait correspondre un élément b,

• l'élément b est appelé l'image de a
• l'élément a est appelé un antécédent de b

Exemple: 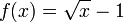$f(x)=\sqrt{x}-1$ Avec x = 0,1,4,9, on a $f(0)=-1 , \;f(1)=0 , \;f(4)=1 , \;f(9)=2$

on dira

1 est l'image de 4 par f

9 est un antécédent de 2 par f

Exemples

Une fonction est donc un outil ayant un ensemble de départ et un ensemble d'arrivée, faisant correspondre aux éléments du premier des éléments du second.

Exemple 1

Une fonction permet de transformer un nombre réel en un autre par exemple, en lui appliquant une suite d'opérations qui doit rester identique pour chaque nombre.

Dans ce cas l'ensemble de départ est $\mathbb{R}$, l'ensemble de définition est l'ensemble des réels pour lesquels on peut appliquer la suite d'opérations, et l'ensemble d'arrivée est $\mathbb{R}$.

Si la suite d'opérations consiste à élever au carré, ôter 4 et prendre l'inverse, on crée une fonction

• Ensemble de départ : $\mathbb{R}\setminus\{-2; 2\}$
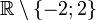
• Domaine de définition : tous les réels différents de − 2 et 2
• Ensemble d'arrivée : $\mathbb{R}$
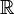
• Correspondance : à x, on associe $\dfrac{1}{x^2-4}$

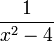
l'image de 3 est $\dfrac{1}{5}$, les antécédents de $\dfrac{1}{5}$ sont 3 et − 3

Exemple 2

Une fonction permet aussi d'associer des points à d'autres points à partir de considérations géométriques.

Dans ce cas l'ensemble de départ est l'ensemble des points du plan (ou de l'espace), l'ensemble d'arrivée est l'ensemble des points du plan (ou de l'espace)

Par exemple si A et B sont deux points différents, on peut associer, à tout point M non situé sur (AB) le point N tel que AMBN soit un parallélogramme

• Ensemble de départ $\mathcal P$
• Ensemble de définition $\mathcal P - (AB)$
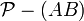
• Ensemble d'arrivée$\mathcal P$
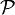
• Correspondance : à M, on associe N tel que AMBN soit un parallélogramme.

Nom

Les fonctions souvent utilisées finissent par porter des noms spécifiques (sin, cos...), les autres s'appellent f, g, etc. L'image d'un élément a pour la fonction f est alors notée f(a).

Notation

Pour résumer toutes ces informations, on utilise l'écriture suivante

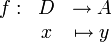$\begin{matrix}f: & D & \rightarrow A\\ & x & \mapsto y\\\end{matrix}$ avec y = f(x) où D représente l'ensemble de départ et A l'ensemble d'arrivée.

La recherche du domaine de définition, si celui-ci est plus petit que l'ensemble de départ, reste faire.

Parfois, on se contente de l'écriture abusive y = f(x) en oubliant tout le reste. Ce qui peut conduire parfois à des confusions dangereuses si on simplifie trop vite, comme le signalait Gottlob Frege dans Qu’est-ce qu’une fonction ?.

• exemple subtil : la fonction 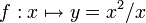$f:x\mapsto y=x^2/x$ et la fonction 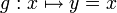$g:x\mapsto y=x$ ne sont pas les mêmes; puisque f est « interdite pour x=0 ».

Ce document provient de « Fonction (math%C3%A9matiques %C3%A9l%C3%A9mentaires) ».