Algorithmes d'optimisation
- Algorithmes d'optimisation
-
Algorithme d'optimisation
Les algorithmes d’optimisation cherchent à déterminer le jeu de paramètres d’entrée d’une fonction donnant à cette fonction la valeur maximale ou minimale. On cherchera par exemple la découpe optimale d’une tôle pour en fabriquer le plus grand nombre de boîtes de conserve possible (ou d’un tissu pour en faire le plus grand nombre de chemises possibles, etc.). Cette optimisation peut se faire sans contrainte ou sous contrainte, le second cas se ramenant au premier dans le cas des fonctions dérivables par la méthode du multiplicateur de Lagrange (et des fonctions non-dérivables par l’algorithme d’Everett).
Le problème est insoluble en tant que tel si l’on ne connaît rien de la fonction (il existe peut-être une combinaison très particulière de valeurs d’entrées lui donnant ponctuellement une valeur extrêmement haute ou basse, qui pourrait échapper à l’algorithme. Aussi existe-t-il plusieurs classes d’algorithmes liés aux différentes connaissances qu’on peut avoir sur la fonction. Si celle-ci est dérivable, l’une des plus performantes est celle du gradient conjugué.
Aucune méthode connue en 2004 (à part l’énumération exhaustive ou l’analyse algébrique) ne permet de trouver avec certitude un extremum global d’une fonction. Les extrema déterminables sont toujours locaux à un domaine, et demandent souvent même en ce cas quelques caractéristiques à la fonction, par exemple dans certains cas la continuité.
Les métaheuristiques sont une classe d’algorithmes d’optimisation qui tentent d’obtenir une valeur approchée de l’optimum global dans le cas de problèmes d’optimisation difficile. Elles ne donnent cependant aucunes garanties sur la fiabilité du résultat.
Détails
- Soit A l’algorithme du problème d’optimisation associé au problème de décision P.
- Opt(i) est la solution optimale pour l’instance i du problème P.
- Cout(i) est la valeur k' de la solution j.
- A est polynomial et on a :
- A :
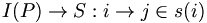 , tel que CP(i,j) = oui.
, tel que CP(i,j) = oui.
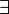 c, constante ne dépendant pas de i, telle que:
c, constante ne dépendant pas de i, telle que:
Catégorie : Algorithme d'optimisation
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Algorithmes d'optimisation de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Optimisation Multidisciplinaire — Sommaire 1 Histoire 2 Les formulations MDO 2.1 Variable de conception 2.2 Contrainte … Wikipédia en Français
Algorithmes de colonie de fourmis — Algorithme de colonies de fourmis Les algorithmes de colonies de fourmis sont des algorithmes inspirés du comportement des fourmis et qui constituent une famille de métaheuristiques d’optimisation. Initialement proposé par Marco Dorigo et al.… … Wikipédia en Français
Optimisation multidisciplinaire — Sommaire 1 Histoire 2 Les formulations MDO 2.1 Variable de conception 2.2 Contrainte 2.3 … Wikipédia en Français
Optimisation (informatique) — Optimisation de code En programmation informatique, l optimisation est la pratique qui consiste généralement à réduire le temps d exécution d une fonction, l espace occupé par les données et le programme, ou la consommation d énergie. La règle… … Wikipédia en Français
Optimisation du code — Optimisation de code En programmation informatique, l optimisation est la pratique qui consiste généralement à réduire le temps d exécution d une fonction, l espace occupé par les données et le programme, ou la consommation d énergie. La règle… … Wikipédia en Français
Optimisation des moteurs de recherche — Optimisation pour les moteurs de recherche L optimisation pour les moteurs de recherche, appelé aussi SEO (de l anglais Search engine optimization) est un ensemble de techniques visant à favoriser la compréhension de la thématique et du contenu d … Wikipédia en Français
Optimisation du référencement — Optimisation pour les moteurs de recherche L optimisation pour les moteurs de recherche, appelé aussi SEO (de l anglais Search engine optimization) est un ensemble de techniques visant à favoriser la compréhension de la thématique et du contenu d … Wikipédia en Français
Optimisation (mathematiques) — Optimisation (mathématiques) En mathématiques, l optimisation est l’étude des problèmes qui sont de la forme : Étant donné : une fonction d’un ensemble A dans l ensemble des nombre réels Rechercher : un élément x0 de A tel que pour … Wikipédia en Français
OPTIMISATION ET CONTRÔLE — L’avènement du calcul différentiel, au XVIIe siècle, a permis de caractériser le minimum d’une fonction f par l’équation f (x ) = 0. On résolvait ainsi d’un coup une foule de problèmes pratiques, tout en soulevant de grandes questions théoriques … Encyclopédie Universelle
Optimisation linéaire — En optimisation, qui est une branche des mathématiques, un problème d optimisation linéaire est un problème d optimisation dans lequel on minimise une fonction linéaire sur un polyèdre convexe. La fonction coût et les contraintes peuvent donc… … Wikipédia en Français
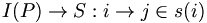 , tel que CP(i,j) = oui.
, tel que CP(i,j) = oui. c, constante ne dépendant pas de i, telle que:
c, constante ne dépendant pas de i, telle que: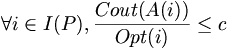 Catégorie : Algorithme d'optimisation
Catégorie : Algorithme d'optimisation