- Algorithme de cantor-zassenhaus
-
Algorithme de Cantor-Zassenhaus
L'algorithme de Cantor-Zassenhaus est un algorithme de factorisation des polynômes à coefficients dans un corps fini Il a été découvert par D. Cantor et Hans Zassenhaus en 1981. Un autre algorithme effectuant cette opération est l'algorithme de Berlekamp, qui date de 1967.
Préparation
L'algorithme fonctionne sur des polynômes sans facteur carré, et dont tous les facteurs premiers ont même degré. La première condition est habituelle, et on s'y ramène en considérant le pgcd du polynôme et de son polynôme dérivé. Quant à la deuxième condition, elle est traitée grâce au fait que tous les polynômes irréductibles de degré divisant n, à coefficients dans un corps fini de cardinal q, sont des diviseurs du polynôme Xqn-X.
Soit f un polynôme sans facteur carré à factoriser. L'algorithme de Cantor-Zassenhaus implique donc de calculer d'abord le pgcd de f et Xq-X, c'est un produit de polynômes de degré 1, auxquels on applique le pas général de l'algorithme ; on divise ensuite f par tous ses facteurs de degré 1 , et on recommence en calculant le pgcd du quotient avec Xq2-X, en divisant par les facteurs trouvés, et en continuant jusqu'à épuisement des facteurs premiers de f.
Pas général de l'algorithme
On suppose ici que f est un polynôme à coefficients dans le corps fini
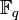 à q éléments, sans facteur carré et dont tous les facteurs premiers sont de même degré d, fixé à l'avance. Notons f1, jusqu'à fr ces facteurs premiers. Alors, par le théorème des restes chinois, il existe un isomorphisme :
à q éléments, sans facteur carré et dont tous les facteurs premiers sont de même degré d, fixé à l'avance. Notons f1, jusqu'à fr ces facteurs premiers. Alors, par le théorème des restes chinois, il existe un isomorphisme :On cherche alors un polynôme a(x), dont la réduction modulo fi sera notée ai pour chaque i, tel que tous les ai valent 0, 1, ou -1, et tel que deux au moins des ensembles suivants sont non vides :
- A = {i | ai(x) = 0},
- B = {i | ai(x) = − 1},
- C = {i | ai(x) = 1},
Alors, les polynômes suivant fournissent une factorisation non triviale de f :
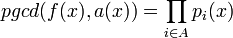 ,
,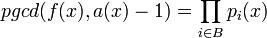 ,
,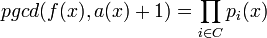 .
.
Il faudra alors appliquer ce pas général récursivement aux facteurs trouvés jusqu'à obtenir des facteurs de degré d. En caractéristique différente de 2, un polynôme a(x) est trouvé en constatant que chaque
![\mathbb{F}_q[x]/(f_i)](/pictures/frwiki/102/fc810e8c2947e154fdfd25bf1ff9f107.png) est un corps fini de cardinal qd, et que donc, en choisissant b(x) de degré plus petit que d, et différent des polynômes constants 0,1, et -1, les réductions ai du polynôme
est un corps fini de cardinal qd, et que donc, en choisissant b(x) de degré plus petit que d, et différent des polynômes constants 0,1, et -1, les réductions ai du polynôme 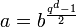 sont bien toutes 0, 1 ou -1. Il peut cependant advenir que pour le polynôme a ainsi construit, deux des trois ensembles A, B et C soient vides, mais la probabilité peut être contrôlée. L'algorithme consiste donc à tester des polynômes b choisis au hasard jusqu'à trouver un polynôme a tel que souhaité.
sont bien toutes 0, 1 ou -1. Il peut cependant advenir que pour le polynôme a ainsi construit, deux des trois ensembles A, B et C soient vides, mais la probabilité peut être contrôlée. L'algorithme consiste donc à tester des polynômes b choisis au hasard jusqu'à trouver un polynôme a tel que souhaité.Référence
Michel Demazure, Cours d'algèbre. Primalité Divisibilité. Codes [détail des éditions]
- Portail des mathématiques
Catégories : Corps fini | Algorithme
Wikimedia Foundation. 2010.

![\mathbb{F}_q[x]/(f)\simeq \mathbb{F}_q[x]/(f_1)\oplus\dots\oplus \mathbb{F}_q[x]/(f_r)](/pictures/frwiki/52/483dc3e3d50d4cb5f01abec4c0f1b32b.png)