Homotopie

Les deux jeux de lettres : bleu et rouge, peuvent être définis par des fonctions homotopes.

L'homotopie est une notion de topologie algébrique. Elle formalise la notion de déformation continue d'un objet à un autre. Deux lacets sont dits homotopes lorsqu'il est possible de passer continument de l'un à l'autre, comme illustré sur la figure de droite. Ce concept se généralise à bien d'autres objets que des lacets. Ainsi, les fonctions définissant les deux jeux de lettres de droite (les bleues et les rouges) sont aussi homotopiques.

L'homotopie fournit des informations sur la nature topologique d'un espace. Une bande circulaire d'un plan ne peut être équivalente, au sens de l'homéomorphisme, à un disque. Dans un disque, tout lacet est homotope à un point. Dans une bande circulaire, ce n'est pas le cas. Cette remarque est source de démonstrations, comme celle du théorème de d'Alembert-Gauss, du point fixe de Brouwer, de Borsuk-Ulam ou encore celle du théorème du sandwich au jambon, qui précise que trois solides mesurables et de mesures finies d'un espace euclidien de dimension trois étant donnés, il existe un hyperplan affine qui sépare chacun des solides en deux parties de mesures égales.

Définition

Homotopie entre deux chemins

Les deux chemins γ₀ et γ₁ sont strictement homotopes.

Soit X un espace topologique. Un chemin continu de X est une application continue du segment réel [0, 1] dans X. Cette définition correspond à l'idée intuitive de chemin, au sens de sentier qui part d'un point pour arriver à un autre.

Deux chemins continus γ₀ et γ₁ de X sont dits homotopes^[1] lorsqu'il existe une application continue H de [0, 1]² dans X telle que l'application qui à t associe H(t, 0) est égale à γ₀ et celle qui à t associe H(t, 1) est égale à γ₁.

$\forall t \in [0,1]\quad H(t,0) = \gamma_0(t)\text{ et } H(t,1) = \gamma_1(t)$

Cette situation ne décrit pas encore exactement la situation représentée à droite. Sur l'illustration, les deux chemins γ₀ et γ₁ possèdent la même origine x ainsi que la même extrémité y. C'est-à-dire :

$\gamma_0(0) = \gamma_1(0) = x \text { et } \gamma_0(1) = \gamma_1(1) = y\;$

Deux chemins continus γ₀ et γ₁ de X ayant même origine et même extrémité, sont dits homotopes strictement lorsqu'ils sont homotopes d'homotopie H et que, pour tout s élément de [0, 1] on dispose des égalités H(0, s) = x et H(1, s) = y^[1].

$\forall s \in [0,1]\quad H(0,s) = x\text{ et } H(1,s) = y$

Homotopie entre deux fonctions

Les définitions précédentes se généralisent à deux fonctions continues f et g d'un espace topologique X dans un espace topologique Y.

Les deux fonctions f et g sont dites homotopes^[2], d'homotopie H, si H est une fonction continue de X×[0, 1] dans Y telle que l'application qui à t associe H(t, 0) est égale à f et celle qui à t associe H(t, 1) est égale à g.

Il est possible de généraliser la deuxième définition. Soit A un sous-ensemble de X tel que les restrictions de f et de g à A soient égales.

Les deux fonctions f et g sont dites homotopes relativement à A si f et g sont homotopes, d'homotopie H et que^[2] :

$\forall s \in [0,1],\; \forall a \in A \quad H(a,s) = f(a) = g(a)$

Exemples

Convexe d'un espace euclidien

Article détaillé : Connexité simple.

Soit E un espace euclidien de dimension n, où n est un entier strictement positif. On dispose de la propriété suivante :

Tout lacet d'ensemble convexe C non vide de E est homotope à un point, c'est-à-dire à un lacet constant^[3].

La figure de droite illustre le cas d'un lacet dans un disque. Ce lacet est manifestement homotope à un point, c'est-à-dire homotope à un lacet constant. Autrement dit, un convexe d'un espace euclidien (plus généralement d'un espace vectoriel topologique localement convexe) est simplement connexe.

Soit A est un élément de C, l'objectif est de montrer que tout lacet γ basé en A (c'est-à-dire ayant pour origine et extrémité A), est homotope au point A. Pour cela on définit une application H : [0 1]² → C définie par :

$\forall t,s \in [0,1]\quad H(t,s)= tA + (1-t)\gamma(s)$

L'application H est manifestement continue, comme γ(x) et A sont deux éléments de C, pour toutes valeurs de t et de s H(t, s) est élément de C car C est convexe. L'application H définit bien une homotopie entre le lacet constant et γ.

Cercle

Dans le cas d'un cercle C, identifié ici aux complexes de module 1, la situation n'est pas équivalente à la précédente. Intuitivement, si un fil parcourt une boucle autour d'un cercle, il n'est pas possible de le ramener à un point sans que le fil ne quitte la surface du cercle et sans le briser. On définit le lacet α comme l'application de [0, 1] dans C, qui à t associe exp(2πi.t) et c le lacet constant qui à t associe 1.

On dispose de la propriété^[4] :

Le lacet du cercle α n'est pas homotope à c.

Cette vérité est en général démontrée dans un résultat plus large, établissant la structure du groupe fondamental du cercle, on peut néanmoins procéder plus directement ici. Intuitivement, si le lacet s'imagine comme un fil qui tourne autour du cercle, tirer suffisamment fort sur les deux brins que l'on trouve au point 1 pour ramener l'intégralité du fil en 1, va casser le fil. Trouver le point de cassure est une méthode pour exhiber une discontinuité.

Démonstration

On raisonne par l'absurde.

Soit H(t, s) une homotopie stricte du lacet α vers c.

Pour une valeur de s donnée, la fonction t → H(t, s) n'est pas toujours surjective, par exemple pour s égal à 1, elle ne l'est pas car elle est constante. Soit N l'ensemble des points s de[0, 1] tel que t → H(t, s) ne soit pas surjectif. Cet ensemble ne contient pas 0, et est ouvert. En effet, si s est élément de N, il existe un point z de du cercle, qui n'est pas atteint par H(., s). L'image de H(., s) est un compact, car H est continue et H(., s) est définie sur un compact. Le complémentaire est ouvert donc z est élément d'un ouvert ne rencontrant pas l'image de H(., s). L'uniforme continuité de H, garantie par le fait que H est continue et définie sur un compact, montre qu'il existe un voisinage de s tel que l'image de H(., s) ne rencontre pas z. Soit s₀ la borne inférieure de la composante connexe de N contenant 1. Cette borne inférieure est au moins égal à 0, strictement inférieure à 1 et ne fait pas partie de N, car N est ouvert.

Un instant s₀ où se produit une déchirure est maintenant connu, il s'agit de trouver le point H(t₀, s₀), indiquant l'endroit où se produit cette déchirure pour trouver une discontinuité.

Pour s élément de ]s₀, 1], on définit N_s comme l'adhérence union des images suivantes :

$\mathcal N_s = \overline {\bigcup_{s_0<\sigma<s} \Big\{z \in \mathcal C,\; \forall t \in [0,1]\quad H(t,\sigma) \neq z\Big\}}$

Soit z₀ un élément de l'intersection I_N des N_s, lorsque s décrit ]s₀, 1]. Comme ces N_s forment un ensemble de fermés emboîtés non vides dans le compact C, l'intersection n'est pas vide et z₀ existe bien. Comme s₀ n'est pas élément de N, la fonction H(.,s₀) est surjective et il existe un élément t₀ tel que H(t₀, s₀) est égal à z₀. Le « point de déchirure » (t₀, s₀) est maintenant trouvé.

Il faut encore montrer que ce « point de déchirure » est bien une discontinuité de H.

On considère les deux points du cercle situés à une distance de 1/2 de z₀ et t₁, t₂ leurs antécédents par la fonction qui à t associe H(t, s₀). Comme H(., s₀) est une fonction surjective, les deux valeurs existent bien. Comme la fonction H est uniformément continue, il existe un réel strictement positif δ, plus petit que 1 - s₀ tel que :

$(1)\quad \forall s \in [s_0,s_0 + \delta[ \quad |H(s_0, t_1) - H(s,t_1)| < \frac 14\quad\text{et}\quad |H(s_0,t_2) - H(s,t_2)| < \frac 14$

Comme z₀ est adhérent à l'ensemble I_N il existe une valeur z à une distance strictement inférieure à 1/4 de z₀ et une valeur σ de l'intervalle ]s₀, s₀ + δ[, tel que H(., σ) ne contienne pas z dans son image. L'image de l'intervalle [t₁, t₂] par la fonction H(., σ) ne contient ni z ni -z, d'après la propriété (1). Sans ces deux points, le cercle contient au moins deux composantes connexes. Les points H(σ, t₁) et H(σ, t₂) sont dans deux composantes connexes distinctes. En conséquence, l'image de l'intervalle [t₁, t₂] par H(σ, .) n'est pas connexe, ce qui montre que H ne peut pas être continu.

Usages

Théorème de d'Alembert-Gauss

L'homotopie est source de nombreuses démonstrations. Un exemple célèbre est celui du théorème de d'Alembert-Gauss qui indique que tout polynôme à coefficients complexes et non constant admet au moins une racine dans C^[5].

Pour le démontrer, on considère un polynôme unitaire p(z) n'ayant aucune racine dans C et on note n son degré. Pour chaque réel positif r, on définit le lacet α_r par :

$\forall t \in [0,1]\quad \alpha_r(t) = \frac {p(r\exp(2\pi i \cdot t))/p(r)}{|p(r\exp(2\pi i \cdot t))/p(r)|}$

Par définition, α_r est un lacet défini sur le cercle. Si r est égal à 0, on obtient le lacet constant égal à 1. Comme la fonction, qui à r et t associe α_r(t) est continue, tous les lacets α_r sont homotopes à un point.

Soit (a_j) la suite presque nulle des coefficients de p et ρ un nombre réel plus grand que 1 et que Σ|a_j| la somme des valeurs absolues des coefficients de p. Si z est un nombre complexe de module égal à ρ :

$(1)\quad |z^n| = \rho^n > (|a_0| + \cdots + |a_{n-1}|)\rho^{n-1} \ge |a_0 + a_1z + \cdots + a_{n-1}z^{n-1}|$

On définit le polynôme p_s(z) et le lacet β_s par :

$p_s(z) = s(a_0 + a_1z + \cdots + a_{n-1}z^{n-1}) + z^n,\quad \forall t \in [0,1]\quad \beta_s(t) = \frac {p_s(\rho\exp(2\pi i \cdot t))/p_s(\rho)}{|p_s(\rho\exp(2\pi i \cdot t))/p_s(\rho)|}$

La majoration (1) montre que le polynôme p_s n'admet pas de racine de module ρ et le lacet β_s est bien défini. Si s est égal à 0, le lacet β₀ fait n tours autour de l'origine, d'après le paragraphe précédent. Comme la fonction si à s et t associe β_s(t) est continue, le lacet β₁ est homotope à β₀. Or le lacet β₁ est égal au lacet α_ρ. Comme le lacet α_ρ est homotope à un point c'est-à-dire qu'il fait 0 tour autour de l'origine, n est égal à 0. Autrement dit, les seuls éventuels polynômes n'ayant pas de racine dans C sont les polynômes constants.

Groupe fondamental

Article détaillé : Groupe fondamental.

Si X est un espace topologique, on peut composer deux lacets de même base p (c'est-à-dire de même origine et même extrémité p) α₁ et α₂ en construisant un lacet parcourant d'abord la trajectoire de α₁, puis celle de α₂. Cette composition est compatible avec la relation d'équivalence est homotope à. Quotienté par cette relation d'équivalence, on obtient une structure de groupe appelé groupe fondamental ou groupe de Poincaré^[6]. Cette notion se généralise et permet de définir une infinité de groupes d'homotopie.

Ce groupe est à l'origine de démonstrations. L'une des plus célèbres est celle du théorème du point fixe de Brouwer en dimension deux, qui indique que toute application continue du disque dans lui-même admet un point fixe^[7].

Topologie algébrique

Article détaillé : Topologie algébrique.

Si trois fermés recouvrent une sphère, l'un au moins contient deux points antipodaux.

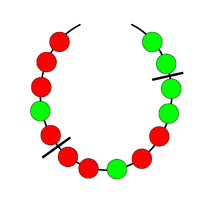
L'homotopie est l'un des outils essentiels de la topologie algébrique^[8]. Le cas le plus simple, celui des lacets est la source de nombreuses démonstrations dans ce domaine. En plus du théorème de d'Alembert-Gauss ou de celui du point fixe de Brouwer, celui de Borsuk-Ulam est caractéristique d'une démarche de la topologie algébrique. En dimension deux, il indique que toute application continue de la sphère dans R² admet deux points antipodaux de même image^[9]. Autrement dit, il existe toujours sur terre deux points situés aux antipodes ayant exactement la même température et la même pression^[10]. Il permet de résoudre par l'affirmative quelques questions célèbres comme celle du sandwich au jambon : existe-il un plan qui coupe trois solides bornés et mesurables (correspondant au jambon, au fromage et au pain d'un sandwich) en deux parties de volumes égaux pour les trois solides^[11] ? Les raisonnements de topologie algébrique faisant usage de l'homotopie permettent aussi de démontrer que si trois fermés ont pour union la sphère, l'un d'entre eux au moins contient deux points antipodaux^[12]. On peut citer encore la question du partage du collier et des deux voleurs : un collier ouvert, illustré à gauche, est formé de perles de deux couleurs différentes, avec un nombre pair de perles de chaque couleur. On montre de façon élémentaire que les deux voleurs peuvent se répartir équitablement les perles en coupant le collier par seulement deux coups de ciseaux. Le théorème de Borsuk-Ulam permet de démontrer que plus généralement, s'il y a t couleurs de perles, t coupes suffisent.

Équivalence homotopique entre espaces topologiques

La notion d'homotopie entre deux fonctions permet de définir une relation d'équivalence entre espaces topologiques :

Deux espaces E et F sont dits homotopiquement équivalents (ou « de même type d'homotopie ») s'il existe deux applications continues $\scriptstyle f:E\to F$ et $\scriptstyle g:F\to E$ telles que :

• $\scriptstyle g\circ f$ est homotope à id_E, l'identité de E ;
• $\scriptstyle f\circ g$ est homotope à id_F, l'identité de F.

Un espace est dit contractile s'il a le même type d'homotopie qu'un point, ou ce qui est équivalent, si son application identité est homotope à une application constante. L'espace ℝⁿ est contractile, ainsi que ses parties convexes, et même ses parties étoilées.

Deux espaces topologiques homéomorphes sont homotopiquement équivalents mais la réciproque est fausse, comme le montrent les exemples suivants :

• mis à part le point lui-même, les espaces contractiles ne sont pas homéomorphes (ni même équipotents) au point ;
• un cercle est homotopiquement équivalent à ℂ* c'est-à-dire un plan privé d'un point, mais ne lui est pas homéomorphe (le cercle privé de deux points n'est pas connexe, tandis que le plan privé de trois points l'est) ;
• l'intervalle réel, le disque dans le plan ou la boule dans ℝ³, de rayon 1, ouverts ou fermés, sont, tous les six, contractiles donc homotopiquement équivalents, mais deux à deux non homéomorphes (par des arguments analogues de connexité ou de simple connexité, voire – pour distinguer les ouverts des fermés – de compacité).

Diverses propriétés importantes en topologie algébrique sont conservées par équivalence homotopique, parmi lesquelles : la simple connexité, la connexité par arcs, les groupes d'homotopie, les groupes d'homologie et de cohomologie…

Isotopie

L’isotopie est un raffinement de l'homotopie ; dans le cas où les deux applications continues $f \, : \, X \rightarrow Y \,\!$ et $g \, : \, X \rightarrow Y \,\!$ sont des homéomorphismes on peut vouloir passer de $f \,\!$ à $g \,\!$, non seulement continûment mais en plus par homéomorphismes.

On dira donc que $f \,\!$ et $g \,\!$ sont isotopes si et seulement s’il existe une application continue $H \, : \, X \times [0,1] \rightarrow Y \,\!$ telle que :

• $\forall x \in X, \, H(x,0) = f(x) \,\!$
• $\forall x \in X, \, H(x,1) = g(x) \,\!$
• pour tout $t \in [0,1] \,\!$ l'application partielle $h_t \,\!$ est un homéomorphisme.

La fonction $h_t \,\!$ est définie par $\forall x \in X, \, h_t(x) = H(x,t) \,\!$.

La notion d'isotopie est notamment importante en théorie des nœuds : deux nœuds sont considérés identiques s'ils sont isotopes, c'est-à-dire si on peut déformer l'un pour obtenir l'autre sans que la « corde » se déchire ou se pénètre.

Notes et références

1. ↑ ^{a et b} On trouve cette définition dans : L. Borel et P. Weiss, Une première approche de l'homotopie dans le cadre continu, cours de Master de l'ENST.
2. ↑ ^{a et b} On trouve cette démonstration dans Lannes 2004, p. 13.
3. ↑ H. Cartan, Cours de C3, Algèbre et géométrie : Groupe fondamental, revêtements, Orsay, 1968-1969, p. 8, traite le cas plus général d'un espace étoilé.
4. ↑ On trouve une approche plus complète qui permet de déterminer le groupe fondamental du cercle dans Lannes 2004, p. 8.
5. ↑ Hatcher 2001, p. 31
6. ↑ Lannes 2004, p. 5
7. ↑ Lannes 2004, p. 11
8. ↑ L'homotopie est qualifiée de main idea of algebraic topology dans Hatcher 2001, p. 1.
9. ↑ D. Leborgne, Calcul différentiel et géométrie, Puf , 1982 (ISBN 2130374956), p. 16
10. ↑ Cette anecdote provient de Hatcher 2001, p. 32.
11. ↑ (en) Jiří Matoušek (de), Using the Borsuk-Ulam Theorem: Lectures on Topological Methods in Combinatorics and Geometry, Springer, 2003 (ISBN 978-3-54000362-5), p. 47 
12. ↑ Ce résultat est une conséquence du théorème de Borsuk-Ulam (Hatcher 2001, p. 33).

• (en) Allen Hatcher (en), Algebraic Topology, Cambridge University Press, 2001 (ISBN 0521795400) 
• J. Lannes, Groupe fondamental, École Polytechnique, 2004 

Articles connexes

• Connexité (mathématiques)
• Homologie, Cohomologie