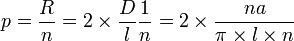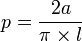- Aiguille de buffon
-
Aiguille de Buffon
L'aiguille de Buffon est une expérience de probabilité proposée en 1733[1] par Georges-Louis Leclerc de Buffon, un scientifique français du XVIIIe siècle. Cette expérience fournit une approximation du nombre Pi. Son analyse met en œuvre un cas simple d'espace de probabilités bidimensionel et continu.
Sommaire
Procédé pratique
Il s'agit de lancer un grand nombre de fois une aiguille sur un parquet. Le parquet est composé de planches parallèles de même largeur. On comptabilise le nombre de fois où l'aiguille tombe à cheval sur [au moins] une rainure du parquet (cas "favorable") par rapport au nombre de lancers totaux. Au fur et à mesure que le nombre de lancers augmente, le quotient se rapproche d'un certain nombre permettant de retrouver π (par exemple, si la longueur de l'aiguille est égale à la largeur d'une planche, ce nombre sera 2⁄π).
Conditions, hypothèses
Pour que l'expérience fonctionne correctement,
- Les lancers successifs doivent être nombreux, indépendants, et on doit considérer une situation d'équiprobabilité (la position de l'aiguille est indifférente, en position et en angle, par rapport au parquet).
- Tous les lancers doivent être reproduits dans des conditions identiques.
Pour que la formule soit simple à calculer,
- La longueur de l'aiguille doit être inférieure ou égale à la largeur d'une planche du parquet.
Étude mathématique
Soient :
- l le réel positif correspondant à la largeur d'une latte de parquet ;
- a le réel positif correspondant à la longueur de l'aiguille ;
- θ le réel compris entre 0 et π / 2 correspondant à l'angle géométrique formé avec les rainures du parquet ;
- r le réel positif correspondant à la distance du centre de l'aiguille à la rainure la plus proche.
D'après les hypothèses, et en utilisant toutes les symétries, on peut considérer que :
- θ suit une loi uniforme continue sur [0;π / 2]
- r suit une loi uniforme continue sur [0;l / 2]
Point de vue géométrique simple
Considérons n lancers (n assez grand) de cette aiguille. On peut considérer alors que toutes le positions différentes de l'aiguille mises bout à bout forme un polygone à n cotés. Plus n est grand plus ce polygone se rapprochera d'un cercle. Le périmètre P de ce cercle vaut alors
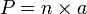 . Le diamètre de ce cercle vaudra
. Le diamètre de ce cercle vaudra 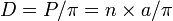 . Le problème revient à savoir : Combien de rainures parallèles sont coupées par le polygone, ou encore combien y a-t-il de rainures à l'intérieur du cercle ?
. Le problème revient à savoir : Combien de rainures parallèles sont coupées par le polygone, ou encore combien y a-t-il de rainures à l'intérieur du cercle ?Le nombre de rainures R coupées est donné par R = 2D / l. Finalement la probabilité que l'aiguille coupe une rainure est donnée par
et en simplifiant
Cas limite
Considérons un lancer isolé. Si l'aiguille touche un point de la rainure avec sa pointe sans la chevaucher, alors on a un triangle rectangle dont l'hypoténuse est la moitié de l'aiguille, un coté est la longueur r, l'autre coté une portion de la rainure. On a alors :
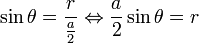
Cas défavorable
Par conséquent, si l'aiguille est pleinement sur une planche, on aura :
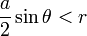
Cas favorable
Si elle chevauche au moins une rainure (la plus proche), on aura :
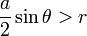
Analyse
On traite ici du cas simple (a < = l).
De même que, pour les probabilités discrètes on forme le quotient des cas "favorables" aux cas "totaux",
on aura dans
![[0;\frac {\pi}2]](/pictures/frwiki/48/0920683d85385d35dfe8492d3a37ec58.png) x
x ![[0;\frac l2]](/pictures/frwiki/50/2800fc3eab2067fd0cafb2bddd663169.png) la probabilité pour une aiguille de tomber sur une rainure l'expression :
la probabilité pour une aiguille de tomber sur une rainure l'expression :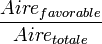
Soit (dessiner l'espace (r,θ) et la limite):
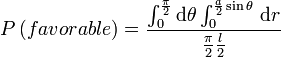
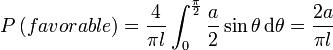
Après une multitude de lancers, d'après la loi des grands nombres, la valeur pratique tendra à se rapprocher de la valeur théorique
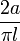 . On peut alors facilement retrouver pi en connaissant les données de l'expérience (l et a).
. On peut alors facilement retrouver pi en connaissant les données de l'expérience (l et a).En effet, soit p la proportion qui estime P : alors on a un estimateur pour
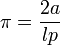
Analyse pour
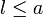
On traite ici du cas où l'aiguille est plus longue que l'écart entre les lames du parquet (penser à des aiguilles à tricoter). Le cas "favorable" est encore : "l'aiguille croise [au moins] une lame de parquet".
Le cas "défavorable" étant plus facile à exprimer mathématiquement, on a (dessiner l'espace (r,θ) et la limite) :
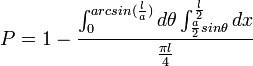
On passe les étapes intermédiaires pour obtenir :
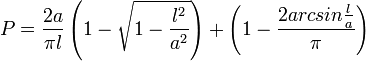
On confirme que pour l = a, on retrouve la formule précédente (établie pour l > = a : une aiguille courte).
La formule permet encore d'estimer π en fonction de (1 − p) où p est la proportion qui estime P puisque (1 − P) a π en facteur (le faire).
En posant
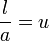 et en développant au voisinage de u = 0, on trouve l'expression de la probabilité pour une très longue aiguille (formule approchée) :
et en développant au voisinage de u = 0, on trouve l'expression de la probabilité pour une très longue aiguille (formule approchée) :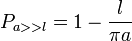
qui tend vers 1 pour a très grand, comme on l'espérait.
Simulation numérique
Erreur en pourcent sur l'estimation de π (un million d'essais) 
0.1 0.2 0.5 1 2 5 10 100 formule exacte 0.4 -0.1 0.1 0.001 -0.1 -0.06 -0.7 1.05 formule approchée - - - - -2 -0.5 -0.3 1.05 Conclusions :
- la meilleure estimation est obtenue pour l = a
- la dégradation de l'estimation est rapide, mais se stabilise rapidement
- l'hypothèse l > = a n'est pas nécessaire pour conduire l'expérience
- la formule approchée (pour a grand) donne de bons résultats dans son domaine d'application
Programme (python) de simulation
# let l=2, we must generate a uniform x in [0,1] # we must also generate a uniform theta in [0, pi/2] # we have : # success if sin(theta) > 2x/a # failure otherwise import random import math Max=1000000 for a in [0.2, 0.4, 1, 2, 4, 10, 20, 200]: Count=0 for i in range(Max): x=random.uniform(0,1) t=random.uniform(0,1)*math.pi/2 if math.sin(t)>2*x/float(a): Count+=1 if a <=2: print a/2.,100*((a/(float(Count)/float(Max)))-math.pi)/math.pi else: P=float(Count)/float(Max) print a/2.,100*(float(a)/(P-1.)*(1.-math.sqrt(1-(2/float(a))*(2/float(a))))-2/(P-1.)*math.asin(2./float(a))-math.pi)/math.pi print a/2.,100.*(2/float(a)/(1.-P)-math.pi)/math.piNotes et références
- ↑ Mémoire sur le jeu du Franc Carreau, présenté à l’Académie des Sciences (1733)
Voir aussi
Articles connexes
Bibliographie
- Martin Aigner et Günter M. Ziegler (trad. Nicolas Puech), Raisonnements divins : quelques démonstrations mathematiques particulièrement élégantes, Springer Verlag, 2e éd., 2006, 270 p. (ISBN 2287338454).
Liens externes
- Un applet Java qui permet de simuler l'expérience de l'aiguille de Buffon
- Un site qui mentionne le fait qu'une expérience de probabilité censée produire un quotient (dans Q) amène π (dans R)
- Portail des probabilités et des statistiques
Catégories : Probabilités | Loi de probabilité | Statistiques | Hasard et aléatoire
Wikimedia Foundation. 2010.