- Extension Cyclotomique
-
Extension cyclotomique
En théorie algébrique des nombres, on appelle extension cyclotomique du corps
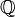 des nombres rationnels, les surcorps de la forme
des nombres rationnels, les surcorps de la forme 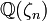 où ζn est une racine primitive nème de l'unité ; cette appellation provient de ce que ces extensions sont des corps de décomposition des polynômes cyclotomiques.
où ζn est une racine primitive nème de l'unité ; cette appellation provient de ce que ces extensions sont des corps de décomposition des polynômes cyclotomiques.Ces corps jouent un rôle crucial, d'une part dans la compréhension de certaines équations diophantiennes : par exemple, l'arithmétique (groupe des classes, notamment) de leur anneau des entiers permet de montrer le dernier théorème de Fermat dans de nombreux cas (voir nombre premier régulier) ; mais aussi, dans la compréhension des extensions algébriques de
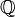 , ce qui peut être considéré comme une version abstraite du problème précédent : le théorème de Kronecker-Weber, par exemple, assure que toute extension abélienne est contenue dans une extension cyclotomique. Enfin, la théorie d'Iwasawa permet d'étudier ces extensions cyclotomiques, en ne les considérant plus séparément, mais comme des familles cohérentes.
, ce qui peut être considéré comme une version abstraite du problème précédent : le théorème de Kronecker-Weber, par exemple, assure que toute extension abélienne est contenue dans une extension cyclotomique. Enfin, la théorie d'Iwasawa permet d'étudier ces extensions cyclotomiques, en ne les considérant plus séparément, mais comme des familles cohérentes.Les extensions cyclotomiques, peuvent aussi être définies pour d'autres corps :
- pour les corps finis, la théorie est essentiellement complète.
- pour les corps locaux de caractéristique 0, elle est mieux comprise que pour le cas global.
- pour les corps de fonctions ...
Sommaire
Premières propriétés en vrac
- L'anneau des entiers du corps
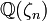 est l'anneau
est l'anneau ![\mathbb{Z}[\zeta_n]](/pictures/frwiki/53/5fcabdadf4b1dc440441ffbc261fe6c3.png) .
. - Les nombres premiers qui ramifient dans l'extension
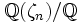 sont exactement les diviseurs de n.
sont exactement les diviseurs de n. - L'extension
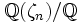 est de degré φ(n), où φ désigne la fonction indicatrice d'Euler. Elle est galoisienne, de groupe de Galois
est de degré φ(n), où φ désigne la fonction indicatrice d'Euler. Elle est galoisienne, de groupe de Galois 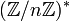 .
. - Le discriminant du corps
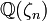 est :
est :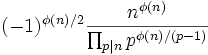
- Le corps
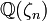 est à multiplication complexe : c'est une extension quadratique totalement imaginaire du corps totalement réel
est à multiplication complexe : c'est une extension quadratique totalement imaginaire du corps totalement réel 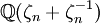 .
.
Quelques questions arithmétiques
On considère le corps
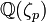 , pour p un nombre premier. Alors, on peut montrer relativement facilement que l'équation :
, pour p un nombre premier. Alors, on peut montrer relativement facilement que l'équation :- xp + yp = zp
n'admet pas de solution (x, y, z) entières non triviales avec xyz premier à p sous l'hypothèse que p ne divise pas le nombre de classes de
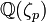 . Un tel nombre premier est appelé nombre premier régulier. Ceci est souvent appelé premier cas du dernier théorème de Fermat, et a été étudié par Ernst Kummer. Kummer a notamment un critère portant sur les nombres de Bernoulli pour déterminer si un nombre premier est régulier. Il est actuellement connu qu'une infinité de nombre premiers ne sont pas réguliers, en revanche, on ne le sait pas s'il en existe une infinité de réguliers.
. Un tel nombre premier est appelé nombre premier régulier. Ceci est souvent appelé premier cas du dernier théorème de Fermat, et a été étudié par Ernst Kummer. Kummer a notamment un critère portant sur les nombres de Bernoulli pour déterminer si un nombre premier est régulier. Il est actuellement connu qu'une infinité de nombre premiers ne sont pas réguliers, en revanche, on ne le sait pas s'il en existe une infinité de réguliers.Plus précisément, on peut se demander pour quelles valeurs de n l'anneau
![\mathbb{Z}[\zeta_n]](/pictures/frwiki/53/5fcabdadf4b1dc440441ffbc261fe6c3.png) est principal, c'est-à-dire que le nombre de classes est 1. Ceci est connu : les seuls nombres n tels que
est principal, c'est-à-dire que le nombre de classes est 1. Ceci est connu : les seuls nombres n tels que 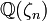 a pour nombre de classes 1 sont 1, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15, 16, 17, 19, 20, 21, 24, 25, 27, 28, 32, 33, 35, 36, 40, 44, 45, 48, 60, 84.
a pour nombre de classes 1 sont 1, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15, 16, 17, 19, 20, 21, 24, 25, 27, 28, 32, 33, 35, 36, 40, 44, 45, 48, 60, 84.Action de la conjugaison complexe
Le fait que le corps soit CM permet de faire agir
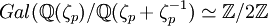 sur les différents objets arithmétiques liés à
sur les différents objets arithmétiques liés à 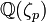 . En particulier, cela permet (voir représentation des groupes) de définir deux parties dans le nombre de classes : la partie + et la partie -. La conjecture de Vandiver s'énonce alors : « pour tout nombre premier p, p ne divise pas la partie + du nombre de classes ». En particulier, un nombre premier régulier vérifie la conjecture de Vandiver. Sous cette hypothèse, et une hypothèse supplémentaire sur les unités du sous-corps réel
. En particulier, cela permet (voir représentation des groupes) de définir deux parties dans le nombre de classes : la partie + et la partie -. La conjecture de Vandiver s'énonce alors : « pour tout nombre premier p, p ne divise pas la partie + du nombre de classes ». En particulier, un nombre premier régulier vérifie la conjecture de Vandiver. Sous cette hypothèse, et une hypothèse supplémentaire sur les unités du sous-corps réel 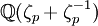 , on peut montrer le deuxième cas du théorème de Fermat : xp + yp = zp n'admet pas de solutions entières non triviales avec
, on peut montrer le deuxième cas du théorème de Fermat : xp + yp = zp n'admet pas de solutions entières non triviales avec 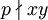 et
et 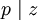 .
.La conjecture de Vandiver est à l'heure actuelle encore une conjecture. Elle a été vérifiée numériquement pour p<4000000.
Extensions cyclotomiques infinies
Pour chaque corps de nombres, et chaque nombre premier p, une tour infinie d'extension peut être considérée : la
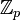 -extension cyclotomique. Si p est impair, la
-extension cyclotomique. Si p est impair, la 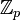 -extension cyclotomique de
-extension cyclotomique de 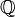 est la tour d'extensions
est la tour d'extensions 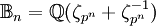 , où
, où 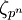 est une racine primitive pnème de l'unité.
est une racine primitive pnème de l'unité. 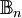 peut encore être vu comme la sous-extension totalement réelle maximale de
peut encore être vu comme la sous-extension totalement réelle maximale de 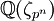 , ou encore, via la correspondance de Galois comme la sous-extension fixée par
, ou encore, via la correspondance de Galois comme la sous-extension fixée par 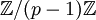 , vu comme sous groupe de
, vu comme sous groupe de 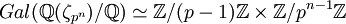 . Le corps
. Le corps 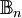 est ainsi une extension galoisienne de
est ainsi une extension galoisienne de 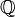 , et même cyclique d'ordre pn ; par définition de la limite projective, la réunion des
, et même cyclique d'ordre pn ; par définition de la limite projective, la réunion des 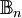 est alors galoisienne sur
est alors galoisienne sur 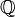 de groupe de Galois
de groupe de Galois 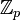 , d'où l'appellation.
, d'où l'appellation.La
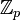 -extension cyclotomique d'un corps de nombres quelconque est obtenu par compositum avec celle-ci.
-extension cyclotomique d'un corps de nombres quelconque est obtenu par compositum avec celle-ci.Référence
(en) Lawrence C. Washington, Introduction to cyclotomic fields [détail des éditions]
- Portail des mathématiques
Catégorie : Corps cyclotomiques
Wikimedia Foundation. 2010.
