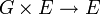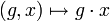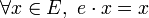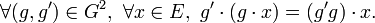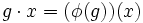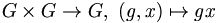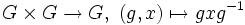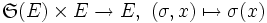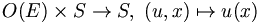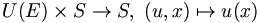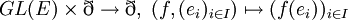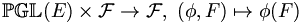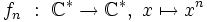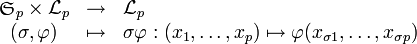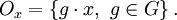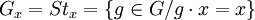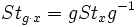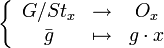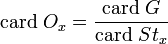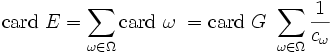- Actions de groupes
-
Action de groupe (mathématiques)
 Pour les articles homonymes, voir Action de groupe.
Pour les articles homonymes, voir Action de groupe.Une action de groupe est, en mathématiques, une description algébrique d'une famille de transformations géométriques d'un espace, par exemple le groupe des rotations agit sur
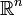 , le groupe de matrices
, le groupe de matrices 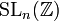 agit sur l'espace
agit sur l'espace 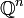 .
.Sommaire
Définition
Étant donné un groupe G, dont la loi est notée multiplicativement et dont l'élément neutre est noté e, on peut définir une action (ou opération) de G sur un ensemble E par une application :
vérifiant les propriétés suivantes :
Dans ce cas on dit également que G opère (ou agit) sur l'ensemble E. Il est important de bien vérifier que l'ensemble E est stable sous l'action du groupe G.
Un point de vue équivalent consiste à dire que le groupe G opère sur l'ensemble E si l'on dispose d'un morphisme de groupes, dit associé à l'action,
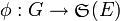 , du groupe dans le groupe symétrique de l'ensemble. Un tel morphisme est appelé une représentation du groupe G.
, du groupe dans le groupe symétrique de l'ensemble. Un tel morphisme est appelé une représentation du groupe G.Ce morphisme est lié à l'action par
pour tous
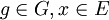 .
.Exemples
- Un groupe opère sur lui-même de deux manières fondamentales :
-
- par translation à gauche, cette action est libre et transitive:
- par automorphisme intérieur, action aussi appelée par conjugaison :
- Le groupe symétrique d'un ensemble E opère naturellement sur E, cette action est fidèle et transitive :
- Le groupe orthogonal (resp. unitaire) d'un espace euclidien (resp. espace hermitien) E opère sur sa sphère unité :
- Le groupe linéaire d'un espace vectoriel de dimension finie E opère sur l'ensemble de ses bases
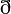 , cette action est libre et transitive :
, cette action est libre et transitive :
- Le groupe projectif (ou groupe des homographies)
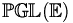 d'un espace projectif
d'un espace projectif 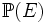 opère sur l'ensemble
opère sur l'ensemble 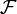 de ses faisceaux harmoniques :
de ses faisceaux harmoniques :
- Si pour tout entier relatif n on définit
alors le groupe
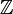 opère sur
opère sur 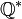 :
: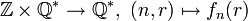 . Cette action est fidèle, mais pas transitive.
. Cette action est fidèle, mais pas transitive.
- Le groupe des permutations opère sur l'ensemble des formes p-linéaires par :
Orbites, stabilisateurs et points fixes
Orbite d'un élément
On définit l'orbite d'un élément x de E par
L'orbite de x est l'ensemble des positions (dans E) susceptibles d'être occupées par l'image de x sous l'action de G. La relation « y est dans l'orbite de x » est une relation d'équivalence sur E, les classes d'équivalences sont les orbites.
En particulier, les orbites forment une partition de E.
Stabilisateur d'un élément
Le stabilisateur d'un élément x de E est l'ensemble
des éléments qui laissent x invariant sous leur action. C'est un sous-groupe de G. Les stabilisateurs de deux éléments de la même orbite sont isomorphes via la formule :
L'application
est une bijection de G / Stx sur Ox.
Points fixes d'un élément du groupe
On peut définir, de manière analogue, l'ensemble Fixg des points fixés par un élément
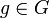 comme l'ensemble des éléments de E invariants sous l'action de g.
comme l'ensemble des éléments de E invariants sous l'action de g.Caractéristiques des actions de groupe
Action transitive
Une action est dite transitive si elle possède une seule orbite. Autrement dit, deux éléments quelconques de l'espace peuvent être envoyés l'un sur l'autre par l'action d'un élément du groupe :
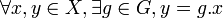 .
.Action libre
Une action est dite libre si tous les stabilisateurs sont réduits au neutre, autrement dit si tout élément différent du neutre agit sans point fixe :
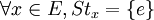 .
.Action fidèle
Une action est dite fidèle si l'intersection des stabilisateurs de tous les éléments est réduite au neutre. Une action libre est fidèle.
Action simplement transitive
Ce terme est peu usité car il a été l'objet de plusieurs controverses sur son interprétation. Pour certains, cela signifie que l'action n'est que transitive, pour d'autres qu'elle est au moins transitive mais a d'autres propriétés, notamment celle d'être une action directe. Enfin, une troisième école affirme que l'action est à la fois transitive et simple, tout en affirmant que "simplement transitive" est légèrement (pas au sens d'une action légère) différente d'une action "librement transitive". Toutefois cette école s'est elle-même divisée entre ceux qui prenaient "librement transitive" au sens de libre et transitive, et ceux qui y voyaient une nuance, et de taille, dans la mesure ou la terminologie "simplement transitive" renvoie à des axiomes différents par deux aspects : on ajoute aux axiomes qui définissent une action transitivement simple l'hypothèse que l'action est légèrement différente ; il restait donc à ce courant de bien définir cette action.
Formule des classes, formule de Burnside
À travers les notions d'orbite et de stabilisateur, les actions de groupe sont un outil commode en combinatoire. D'autre part, un certain nombre de propriétés concernant la structure de certains groupes peuvent être démontrées par des arguments de dénombrement.
Deux identités reviennent fréquemment. Lorsque l'ensemble E et le groupe G sont finis, la formule des classes affirme que pour toute orbite Ox
Remarquons que les stabilisateurs de 2 éléments d'une même orbite sont conjugués et ont donc le même cardinal (on peut donc remplacer dans la formule ci-dessus x par n'importe quel élément de l'orbite.
Par suite si on désigne par Ω l'ensemble des orbites et par cω le cardinal commun des stabilisateurs des éléments de l'orbite ω on peut écrire:
Cette formule relie le cardinal de l'ensemble à la structure du groupe G.
La formule de Burnside affirme pour sa part (toujours sous l'hypothèse que E et G sont finis) que le nombre d'orbites est
-
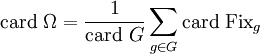 .
.
En particulier, si G est un groupe fini agissant transitivement sur un ensemble non vide E, alors la moyenne du nombre de points fixes des éléments du groupe G est égale à 1.
DémonstrationsFormule des classes
- x étant fixé dans
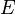 , soit dans
, soit dans 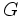 la relation d'équivalence
la relation d'équivalence 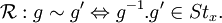 Les classes d'équivalence ne sont autres que les classes à gauche pour
Les classes d'équivalence ne sont autres que les classes à gauche pour 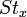 .
.
Ces classes ont donc toutes le même cardinal, celui de
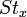 .
.Soit γ l'application de
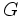 dans Ox, orbite de x :
dans Ox, orbite de x : 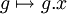 .
.Deux éléments de
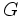 ont même image par γ si et seulement s'ils sont équivalents selon
ont même image par γ si et seulement s'ils sont équivalents selon 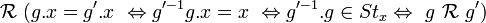 . On peut donc effectuer la factorisation canonique
. On peut donc effectuer la factorisation canonique 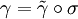 où σ désigne la surjection canonique de
où σ désigne la surjection canonique de 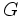 sur
sur 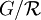 et
et 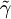 l'injection quotient qui est en réalité bijective puisque γ est surjective (par définition même de l'orbite). Il en résulte immédiatement la formule annoncée :
l'injection quotient qui est en réalité bijective puisque γ est surjective (par définition même de l'orbite). Il en résulte immédiatement la formule annoncée : 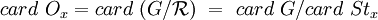 .
.Formule de Burnside
- Soit
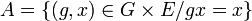 .
.
On peut écrire en désignant par Ω l'ensemble des orbites:
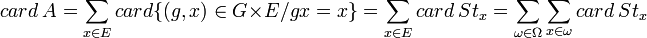
Mais les stabilisateurs de 2 éléments d'une même orbite sont conjugués (l'un est l'image de l'autre par un automorphisme intérieur) et ont donc le même cardinal. Donc en désignant par cω ce cardinal:
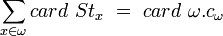 . Il résulte alors de la formule des classes (cf. ci-dessus) que
. Il résulte alors de la formule des classes (cf. ci-dessus) que 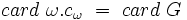 .
.Donc
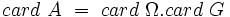 .
.Mais on peut aussi calculer card A en groupant différemment les éléments:
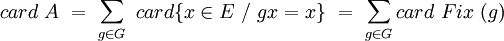
Et en écrivant l'égalité des 2 expressions de
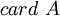 trouvées, on obtient la formule demandée:
trouvées, on obtient la formule demandée: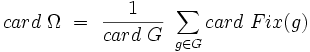
Voir aussi
- Portail des mathématiques
Catégorie : Action de groupes -
Wikimedia Foundation. 2010.