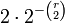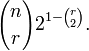Combinatoire probabiliste

Méthode probabiliste

Cet article n'est pas sur les systèmes de preuve interactive qui sont utilisés pour convaincre un vérificateur qu'une démonstration est correcte, ni sur les algorithmes probabilistes, qui donnent la bonne réponse avec une grande probabilité, mais pas avec certitude, ni sur les méthodes de Monte-Carlo.

La méthode probabiliste est une méthode nonconstructive, principalement utilisés dans la combinatoire et lancé par Paul Erdös, pour démontrer l'existence d'un certain type d'objet mathématique. Cette méthode a été appliquée à d'autres domaines de mathématiques tels que la théorie des nombres, l'algèbre linéaire et analyse réelle. Il travaille en montrant que si l'on choisit au hasard des objets d'une catégorie, la probabilité que le résultat est de la certain type est plus que zéro. Bien que la démonstration utilise la probabilité, la conclusion finale est déterminée pour certains, sans aucune erreur possible.

Introduction

Si chaque objet dans une collection d'objets ne parvient pas à avoir une certaine propriété, alors la probabilité qu'un objet choisi au hasard à partir de la collection a cette propriété est zéro. S'agissant de ce gaz, si la probabilité que l'objet au hasard a la propriété est supérieure à zéro, cela démontre l'existence d'au moins un objet dans la collection qui a la propriété. Il n'a pas d'importance si la probabilité est extrêmement faible; toute probabilité positive est acceptable.

De même, ce qui montre que la probabilité est (strictement) moins de 1 peut être utilisé pour démontrer l'existence d'un objet qui ne satisfait pas les propriétés.

Une autre façon d'utiliser la méthode probabiliste est par le calcul de l'espérance de certaine variable aléatoire. S'il peut être démontré que la variable aléatoire peut prendre une valeur inférieure à l'espérance, cela démontre que la variable aléatoire peut également prendre sur une valeur supérieure à l'espérance.

Certains outils sont fréquemment utilisés dans la méthode probabiliste sont l'inégalité de Markov, l'inégalité de Chernoff, et le lemme local de Lovász.

Deux exemples dus à Erdős

Bien que d'autres avant lui aient démontré des théorèmes en s'appuyant sur la méthode probabiliste^[1], la plupart des démonstrations utilisant cette méthode sont à mettre au crédit d'Erdős. Le premier exemple publié en 1947 donne une démonstration d'une limite inférieure pour le nombre de Ramsey R(r, r; 2).

Premier exemple

Supposons que nous ayons un graphe complet sur n sommets et que nous voulions démontrer (pour les valeurs assez petites de n) qu'il est possible de colorer les arêtes du graphe en deux couleurs (par exemple rouge et bleu), de sorte qu'il n'y ait pas de sous-graphe complet sur r sommets qui soit monochromatique (toutes les arêtes de même couleur).

Pour ce faire, colorions le graphe de façon aléatoire, c'est-à-dire colorions chaque arête de façon indépendante, avec probabilité ½ d'être rouge et ½ d'être bleu. Calculons le nombre de sous-graphes monochromatiques sur r sommets comme suit:

• Pour tout ensemble S de r sommets de notre graphe, affectons à la variable X(S) la valeur 1 si toutes les arêtes entre les r sommets sont de la même couleur et la valeur 0 autrement. Notons que le nombre de r-sous-graphes monochromatiques est la somme des X(S) quand S parcourt tous les sous-ensembles. Pour tout S, l'espérance de X(S) est la probabilité que toutes les 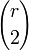${r \choose 2}$ arêtes de S soient de même couleur,

$2 \cdot 2^{-{r \choose 2}}$

(le facteur 2 provient de ce qu'il y a deux couleurs possibles).

Cela est vrai pour l'une des C(n, r) sous-ensembles nous aurions pu choisir, nous avons donc que la somme de E[X(S)] sur tous S est

${n \choose r}2^{1-{r \choose 2}}.$

La somme de l'espérance est l'espérance de la somme (indépendamment du fait que les variables sont indépendants), de sorte que l'espérance de la somme (l'attendu nombre de r-sous-graphes monochromatiques) est

${n \choose r}2^{1-{r \choose 2}}.$

Pensez à ce qui se passe si cette valeur est inférieure à 1. Le nombre de r-sous-graphes monochromatiques dans notre coloration aléatoire sera toujours un entier, donc il doit être inférieur à l'espérance, pour au moins un des colorations. Mais le seul entier qui satisfait à ce critère est de 0. Ainsi, si

$C(n,r) < 2^{{r \choose 2} - 1}$,

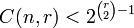puis certains colorations répond à notre critère désirée, donc par définition, R(r, r; 2) doit être plus grande que n. En particulier, R(r, r; 2) doit augmenter au moins exponentielle avec r.

Une particularité de cet argument est qu'il est entièrement nonconstructive. Même s'il démontre (par exemple) que presque tous les colorations de la graphe complet sur (1.1)^r sommets ne contient pas de r-sous-graphe monochromatique, il ne donne pas d'exemple explicite d'une telle coloration. Le problème de trouver une telle coloration a été ouvert à plus de 50 ans.

Deuxième exemple

Un document 1959 par Erdös (voir références citées ci-dessous) a abordé le problème en suivant dans la théorie des graphes: étant donné entiers g et k, existe-t-il un graphe G contenant cycles de longueur au plus g, tels que le nombre chromatique de G est au moins k?

Il peut être démontré que ce type de graphe existe pour tout g et k, et la démonstation est relativement simple. Soit n très grand et envisager un random graph G sur n sommets, où chaque arête dans G existe avec une probabilité n^(1-g)/g. Il peut être démontré que, avec probabilité positive, les deux déclarations suivantes sont vraies:

• G ne contient aucun stable de taille $\lceil n/2k \rceil$
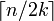
• G contient au plus n/2 cycles de longueur au plus g.

Voici l'astuce: depuis G a ces deux propriétés, on peut supprimer au plus n/2 sommets de G pour obtenir un nouveau graphe G' sur n' sommets qui ne contient pas de cycles de longueur au plus g. Nous pouvons voir que cet nouveau graphe n'a pas un stable de taille 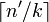$\lceil n'/k \rceil$, donc G' a nombre chromatique au moins k.

Ce résultat donne une indication sur les raisons pour lesquelles le calcul du nombre chromatique d'un graphe est si difficile: même quand il n'y a pas de raisons locales (telles que les petits cycles) d'un graphe d'exiger beaucoup de couleurs le nombre chromatique peut être arbitrairement grande.

Notes

1. ↑ Ainsi, Szele's a montré en 1943 qu'il existe des tournois contenant un grand nombre de cycles hamiltoniens.

Voir aussi

• Graphe aléatoire

Références

• Alon, Noga; Spencer, Joel H. (2000). The probabilistic method (2ed). New York: Wiley-Interscience. ISBN 0-471-37046-0.
• Erdos, P. (1959). Graph theory and probability. Canad. J. Math. 11: 34–38.
• Matoušek, Jirí. http://kam.mff.cuni.cz/~matousek/prob-ln-2pp.ps.gz (gzipped ps file)
• Alon, N and Krivelevich, M (2006). Extremal and Probabilistic Combinatorics

Ce document provient de « M%C3%A9thode probabiliste ».