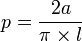- 3,14
-
Pi
 Pour les articles homonymes, voir Pi (homonymie).
Pour les articles homonymes, voir Pi (homonymie). Si le diamètre du cercle est 1, sa circonférence est π.
Si le diamètre du cercle est 1, sa circonférence est π.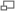
Le nombre pi, noté par la lettre grecque du même nom π (toujours en minuscule) est le rapport constant[1] entre la circonférence d’un cercle et son diamètre. Il est appelé aussi constante d’Archimède.
Le nombre π est aussi le rapport constant entre l’aire d’un disque et le carré de son rayon.
Valeurs approchées courantes : 3,14 ; 3,1416 ; 22/7 ; 355/113
Mais π est un nombre irrationnel, c’est-à-dire qu’il n’est pas le rapport de deux nombres entiers. En fait, ce nombre est transcendant[2]. Ceci signifie qu’il n'existe pas de polynôme non nul à coefficients entiers dont π soit une racine.
La transcendance de π établit l’impossibilité de résoudre le problème de la quadrature du cercle : il est impossible de construire, à l’aide de la règle et du compas seulement, un carré dont la surface est rigoureusement égale à la surface d’un disque donné.
- π ≈ 3,14159265358979323846264338327950288419716939937510
Sommaire
Histoire
Premiers calculs
Il semble que, très tôt, les mathématiciens aient été convaincus qu’il existait un rapport constant entre le périmètre du cercle et son diamètre, ainsi qu’entre l’aire du disque et le carré du rayon. Des tablettes babyloniennes datant de 2000 ans avant J.-C. et découvertes en 1936[3] présentent des calculs d’aire conduisant à une valeur de π de 3+1/8. La tablette propose un premier calcul qui utilise une valeur de π égale à 3. Ce calcul est suivi d’un autre présentant un facteur correctif de 1/(57/60+36/3600).
- Première approximation de π : 3
- Seconde approximation :
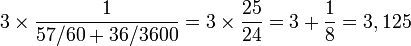
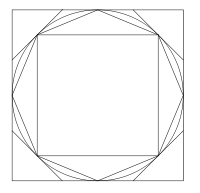
Découvert en 1855, le papyrus de Rhind contient le texte, recopié vers l’an 1650 avant notre ère par le scribe égyptien Ahmès, d’un manuel de problèmes pédagogique plus ancien encore. On y trouve une méthode pour évaluer l’aire d’un disque en prenant le carré dont le côté est égal au diamètre du disque diminué d’un neuvième. Cette méthode conduit à une évaluation de π de 256⁄81. Dans l’illustration ci-contre, le disque a pour diamètre 9. L’aire du disque est légèrement supérieure à l’aire de l’octogone irrégulier obtenu en rognant les coins du carré de côté 9. Cet octogone a pour aire 63, l’aire du disque est alors évaluée à 64 soit l’aire d'un carré de côté 8.
- Autre approximation :

Mais ni chez les Babyloniens, ni chez les Égyptiens, on ne décèle une volonté de mettre en évidence un nombre ni de montrer que le rapport entre l’aire du disque et le carré du rayon est le même que le rapport entre la circonférence du cercle et son diamètre.
- Formule restant à prouver :
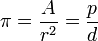
C’est chez Archimède, dans son traité De la mesure du cercle[4] que l’on peut lire une démonstration liant l’aire du disque et l’aire du triangle ayant pour base le périmètre du cercle et pour hauteur le rayon.
- Aire du disque =
 circonférence × rayon =
circonférence × rayon =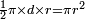
C’est ainsi qu’il prouve que le même nombre s’utilise dans les deux formules. Dans ce même traité, Archimède prouve que le rapport entre le périmètre du cercle et son diamètre est compris entre 3 + 10⁄71 et 3 + 1⁄7.
- Encadrement de π : 3,1408 < π < 3,1429
La première démonstration s’appuie sur la méthode d'exhaustion et un raisonnement par l'absurde. En partant d’un carré inscrit dans le cercle et d’un carré circonscrit au cercle et en multipliant indéfiniment par 2 le nombre de côtés, il prouve que l’aire du disque ne peut être inférieure ni supérieure à celle du triangle correspondant.
Sa démonstration exploite l’idée du découpage en quartiers : le cercle est découpé en plusieurs quartiers qui, mis bout à bout, dessinent des triangles curvilignes de même hauteur. En multipliant le nombre de quartiers, la base des triangles curvilignes est presque droite et la hauteur est proche du rayon, la somme des bases correspond alors au périmètre du cercle et l’aire est alors de 1⁄2 de la base multipliée par la hauteur, c’est-à-dire 1⁄2 du périmètre multiplié par le rayon.
La seconde démonstration consiste à encadrer le périmètre du cercle par le périmètre de polygones réguliers inscrit et circonscrit au cercle et possédant 96 côtés. Pour calculer les périmètres de ces polygones, il part d’hexagones inscrit et circonscrit et met en évidence les formules donnant le périmètre d’un polygone dont le nombre de côté a doublé. Archimède s’arrête à 96 côtés car les calculs qu’il est amené à effectuer, avec valeurs approchées, sont déjà longs pour l’époque. Mais il met en place ainsi une méthode qui sera reprise par ses successeurs et qui peut en théorie être poursuivie indéfiniment.
Formules d'ArchimèdeArchimède utilise une propriété liant le pied d’une bissectrice aux côtés adjacents : Dans la figure ci-contre SS′ est la bissectrice de l’angle de sommet S
Pour le polygone circonscrit. Dans la figure ci-dessous (gauche), c1 et c2 sont les demi-côtés de deux polygones circonscrits consécutifs. Archimède montre, en utilisant la propriété précédente, que
et réitère 4 fois l’opération à partir de l’hexagone.
Pour le polygone inscrit. Dans la figure ci-contre, c1 et c2 sont les côtés de deux polygones inscrits consécutifs. Archimède montre, en utilisant les triangles semblables et la propriété de la bissectrice queDe nos jours, les formules trigonométriques permettent de simplifier l’algorithme d’Archimède. Les périmètres pi et Pi des polygones inscrits et circonscrits vérifient les relations de récurrence suivantes
En effet, pour un cercle de rayon 1, si on note an la moitié de l’angle au centre des polygones à l’étape n, on sait que
et
Ce n’est cependant pas Archimède qui attribue à ce rapport la lettre grecque « π », première lettre des mots grecs περιφέρεια (périphérie) et περίμετρος (périmètre, c'est-à-dire circonférence) mais William Jones en 1706. Cette notation, reprise par Euler en 1736, est définitivement adoptée dès la fin du XVIIIe siècle[5].
À la conquête des décimales
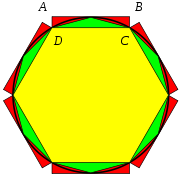 Encadrement de Liu Hui. Méthode développée dans en:Liu Hui's π algorithm.
Encadrement de Liu Hui. Méthode développée dans en:Liu Hui's π algorithm.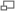
Si les calculs pratiques peuvent se satisfaire de la valeur 3,14 comme bonne approximation de π, la curiosité des mathématiciens les pousse à déterminer ce nombre avec plus de précision. Au IIIe siècle, en Chine, Liu Hui, commentateur des Neuf chapitres, propose comme rapport entre le périmètre et le diamètre la valeur pratique de 3 mais développe des calculs proches de ceux d’Archimède mais plus performants et fournit une approximation de π de 3,1416[6]. Le mathématicien chinois Zu Chongzhi donna une approximation rationnelle encore plus précise de π[7] : π ≈ 355/113 (dont les développement décimaux sont identiques jusqu'à la 6ème décimale, π ≈ 3,1415926 et 355/113 ≈ 3,1415929).
En Perse, en 1429, Al-Kashi calcule 14 décimales de π. En 1596, toujours avec des méthodes géométriques, l’Allemand Ludolph van Ceulen calcule 20 décimales, puis 34 en 1609. Il est si fier de son exploit (il y consacra une bonne partie de sa vie) qu’il demande à ce que le nombre soit gravé sur sa tombe.
Ensuite, grâce au développement de l’analyse au XVIIe siècle, avec notamment les sommes et produits infinis, le calcul des décimales de Pi s’accélère.
James Gregory (1638 - 1675) découvre la formule suivante[8] :
 James Gregory(1638 - 1675)
James Gregory(1638 - 1675)
qui permet en prenant une valeur adéquate pour x de calculer π. Cependant, il ne semble pas que ceci ait interessé Gregory. Il souhaitait, par d'autres moyens, arriver à l'impossibilité de la quadrature du cercle en montrant la transcendance de π, ce qui est exact mais sa méthode était erronée[9].
En fait, la formule de développement en série de la fonction arctan avait déjà été proposée vers 1410 par le mathématicien indien Madhava de Sangamagrama (1350-1425). Celui-ci précise les cas particuliers π/4=arctan(1) et π/6=arctan(1/√3) :
La première série est remarquablement simple mais n'est guère utile pour calculer π. En effet, la précision du calcul est de 1/(2n+1), c’est-à-dire qu’il est nécessaire de calculer 500 termes pour n’avoir une erreur que sur la troisième décimale. La seconde, par contre, fournit une méthode de calcul plus efficace que celle d'Archimède. Elle permet à Madhava de calculer 11 décimales de π[10]. En utilisant cette même série, Sharp en 1699 calcule 71 décimales de π[11].
Isaac Newton calcule 16 décimales en 1665, en utilisant le développement en série de π/6=arcsin 1/2[11].
En 1706, John Machin utilise astucieusement le développement en série de Gregory, en établissant la formule qui porte son nom :
et calcule 100 décimales de π[12].
Vers 1760, Euler calcule 20 décimales en une heure (à comparer avec la trentaine de décimales obtenue par Van Ceulen en plus de 10 ans de calcul). Le mathématicien slovène Jurij Vega calcule en 1789 les 140 premières décimales π parmi lesquelles 137 sont correctes. Ce record tiendra plus de 50 ans. Il améliore la formule que John Machin avait trouvée en 1706 et sa méthode est toujours mentionnée aujourd'hui. Le mathématicien William Shanks passe 20 ans de sa vie à calculer les décimales de Pi. En 1873, à l’aide de la formule de Machin, il présente 707 décimales de π, mais seules les 528 premières sont correctes. À l'occasion de l’exposition universelle de Paris de 1937, celles-ci furent malheureusement gravées dans la salle π du Palais de la Découverte. L’erreur ne sera détectée qu’en 1945, elle est corrigée depuis.
Le calcul des décimales de π s’emballe au XXe siècle avec l’apparition de l’informatique : 2 037 décimales sont calculées en 1949 par le calculateur américain ENIAC, 10 000 décimales sont obtenues en 1958, 100 000 en 1961, 1 000 000 en 1973, 10 000 000 en 1982, 100 000 000 en 1989, puis 1 000 000 000 la même année. En 2002, 1 241 100 000 000 décimales étaient connues.
Les approximations très précises de π sont généralement calculées avec l’algorithme de Gauss-Legendre et l’algorithme de Borwein.
L’algorithme de Salamin-Brent, donnant un très grand nombre de décimales et inventé en 1976, s’appuie sur un vieux résultat pressenti puis démontré par Gauss. En 1818, celui-ci démontre le lien existant entre la moyenne arithmético-géométrique de 1 et √2 (M(1,√2)), la longueur de la lemniscate de Bernoulli et π. La longueur de la lemniscate est
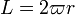 où r représente la distance OA entre le centre et un sommet de la lemniscate et où
où r représente la distance OA entre le centre et un sommet de la lemniscate et où 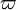 est la constante de la lemniscate. Si on note G, la constante de Gauss, c’est-à-dire l’inverse de M(1,√2) alors
est la constante de la lemniscate. Si on note G, la constante de Gauss, c’est-à-dire l’inverse de M(1,√2) alorsL’Américain Eugène Salamin et l’Australien Richard Brent utilisent ce résultat pour un algorithme donnant les décimales de π dont la convergence est quadratique, c’est-à-dire que le nombre de décimales justes double à chaque étape. La conquête des décimales de π avance alors conjointement avec celle des décimales de √2[13].
On peut voir 1 000 000 de décimales de π et de 1⁄π sur le Projet Gutenberg (voir liens externes).
Le record actuel est de 1 241 100 000 000 de décimales, déterminées après 600 heures de calcul en novembre 2002 sur un supercalculateur parallèle Hitachi à 64 nœuds, avec 1 téraoctet de mémoire centrale, qui pouvait effectuer 2 000 milliards d’opérations en virgule flottante par seconde, soit près de deux fois plus que pour le précédent record (206 milliards de décimales) ; les formules de Machin suivantes ont été utilisées pour cela :
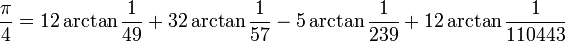 (K. Takano, 1982)
(K. Takano, 1982)
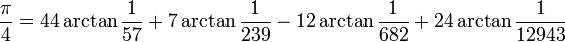 (F. C. W. Störmer, 1896)
(F. C. W. Störmer, 1896)
Ces approximations sont tellement grandes qu’elles n’ont aucune utilisation pratique, si ce n’est tester les nouveaux supercalculateurs.
D’autres méthodes et algorithmes sont actuellement à l’étude et mis en œuvre comme l’utilisation en parallèle d’ordinateurs connectés sur le réseau Internet.
Parallèlement à ces recherches, d'autres algorithmes se mettent en place pour calculer directement la ne décimale de π. En 1995, David Bailey, en collaboration avec Peter Borwein et Simon Plouffe, découvre une nouvelle formule de π, une série (souvent appelée formule BBP) :
Cette formule permet de calculer facilement la ne décimale binaire ou hexadécimale de π, sans avoir à calculer les décimales précédentes. Le site de Bailey[14] en contient la dérivation et l’implémentation dans de nombreux langages de programmation. Grâce à une formule dérivée de la formule BBP, le 4 000 000 000 000 000e chiffre de π en base 2 a été obtenu en 2001.
Un an plus tard, Simon Plouffe met au point un algorithme permettant le calcul de la ne décimale de π, mais cette fois-ci en décimal[15]. Malheureusement, cet algorithme qui permet actuellement de déterminer en base 10 un chiffre précis et isolé de π est moins rapide que celui qui consiste à calculer tous les chiffres décimaux précédents.
De la nature de π
Article détaillé : Quadrature du cercle.Dès l’époque grecque, la question de la quadrature du cercle est posée :
- « Peut-on, uniquement avec une règle non graduée et un compas, construire un carré dont l’aire a même surface que celle d’un disque donné ? »
Le fait que certaines lunules soient quarables a laissé l’espoir aux mathématiciens qu’une telle construction était possible. Réaliser la quadrature du cercle, c’est trouver une méthode permettant, lorsqu'une longueur r est donnée, de construire à la règle et au compas la longueur r√π. Derrière la question de la quadrature du cercle, se pose la question de la nature du nombre π . Les Grecs savaient construire toute longueur en rapport rationnel (rapport de deux entiers) avec une autre, et même la racine carrée de celle-ci. Si π avait été rationnel, le problème aurait été terminé. Mais les Grecs étaient incapables de statuer sur la rationalité ou l’irrationalité de π. De plus, l’irrationalité de π n’aurait prouvé aucune impossibilité pour la construction. En effet, Euclide avait déjà prouvé que √2 était irrationnel ce qui n’empêchait nullement la duplication du carré. Cependant, très rapidement, on pressent qu’un nombre qui ne serait pas solution d’une équation polynomiale à coefficients entiers, c’est-à-dire un nombre transcendant, a peu de chance d’être constructible. Ce pressentiment ne deviendra une certitude que lorsque Pierre-Laurent Wantzel énoncera, en 1837, son théorème sur les nombres constructibles. Une des conséquences de son théorème permet d’affirmer qu’une longueur constructible est toujours un nombre algébrique.
La question à laquelle les mathématiciens doivent répondre est donc double :
- le nombre π est-il rationnel ?
- le nombre π est-il transcendant?
Le développement de π selon la série
laisse soupçonner que π n’est pas rationnel mais sans démonstration rigoureuse à l’appui. Les fractions continues généralisées vont fournir la réponse à la question.
En 1761, dans son Mémoires sur quelques propriétés remarquables des quantités transcendantes, circulaires et logarithmiques, Jean Henri Lambert étudie le développement en fraction continue de tan(x) et montre que, lorsque x est rationnel, le développement en fraction continue de tan(m/n) est
Par conséquent, lorsque x est rationnel, le développement en fraction continue de tan(x) est illimité. Or on sait qu’un développement illimité conduit à un nombre irrationnel. Bref, quand x est rationnel, tan(x) est irrationnel. Or tan(π/4) vaut 1, c’est un rationnel. Par contraposée, on peut affirmer que π/4 n’est pas rationnel.
En 1873, Charles Hermite prouve que la base du logarithme népérien le nombre e est transcendant. En 1882, Ferdinand von Lindemann généralise son raisonnement en un théorème (Théorème d'Hermite-Lindemann) qui stipule que, si x est algébrique, alors ex est transcendant. Or eiπ = -1 donc eiπ n’est pas transcendant. Par contraposée, iπ n’est pas algébrique et π est transcendant.
Mais de nombreuses questions se posent encore : π et e sont deux nombres transcendants mais sont-ils algébriquement indépendant ou bien existe-t-il une équation polynomiale à deux variables et à coefficients entiers dont le couple (π, e) soit solution ? La question est encore en suspens. En 1929, Alexandre O Gel'fond prouve que eπ est transcendant [17] et en 1996, Yuri Nesterenko prouve que π et eπ sont algébriquement indépendants.
Par ailleurs, le développement décimal de π ouvre le champ à d’autres questions
- Existe-t-il un nombre infini de 0 ? de 1 ? de 2 ? etc. dans le développement décimal ?
- Les 10 chiffres de l’écriture décimales sont-ils équirépartis ?
- π est-il un nombre univers ? C’est-à-dire, peut-on trouver dans le développement décimal de π n’importe quelle séquence de chiffres ?
- π est-il un nombre normal ? Les séquences de n chiffres sont-elles équiprobables ?
À ce jour[18], il n'existe pas de réponse à ces questions[19].
π grandeur physique ?
La définition de π comme le rapport constant entre la longueur d’un cercle et son diamètre pourrait laisser penser que cette grandeur est une grandeur physique et qu’il suffirait, pour en déterminer une valeur précise, de prendre un cercle assez grand et d’effectuer les deux mesures correspondantes. On peut, par une expérience de l’esprit, imaginer qu’un Chinois, ou un Babylonien, convaincu de cette méthode, se soit rendu sur une surface suffisamment vaste et plane pour effectuer ces mesures. On peut imaginer qu’il ait poursuivi l’expérience en agrandissant fortement le rayon du cercle. Il aurait alors eu la surprise de constater que ce rapport n’était plus constant mais variable, que ce rapport, proche de 3,14 pour un petit cercle, tendait à diminuer quand le rayon du cercle augmentait de façon significative. En effet, les mesures qu’il aurait effectuées sont des mesures effectuées sur la terre, c’est-à-dire sur une sphère. En géométrie sphérique, le rapport circonférence/diamètre n’est pas constant. Le résultat énoncé précédemment n’est valable qu’en géométrie euclidienne. Les physiciens émettent l’hypothèse que notre univers puisse ne pas être euclidien. Dans ce cas, la circonférence d’un cercle physique ne vaudrait pas π multiplié par le diamètre. Mais, quelle que soit la nature globale de notre univers, la théorie de la relativité indique que les masses déforment localement notre espace. La valeur de π × d comme circonférence d’un cercle physique n’est donc qu’une approximation qui ne nécessite pas tous les efforts de précision sur les décimales. Le nombre π n’est donc qu’une constante mathématique utile dans un espace mathématique euclidien. Cette observation a poussé certains mathématiciens à rechercher une définition de π moins concrète.
Formules incluant π
Les formules intéressantes incluant π sont innombrables et apparaissent dans quasiment tous les domaines des mathématiques et des sciences. Une des plus célèbres après celles relevant de la définition géométrique de π est l’identité d'Euler. Cette formule a été décrite comme la formule la « plus remarquable » pour sa propriété de faire intervenir 1, 0, e, i et bien sûr Pi qui sont parmi les nombres les plus « remarquables » des mathématiques.
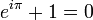
Géométrie
Pi apparaît dans beaucoup de formules de géométrie impliquant les cercles et les sphères
Forme géométrique Formule Circonférence d’un cercle de rayon r et de diamètre d 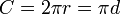
Aire d’un disque de rayon r 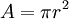
Aire d’une ellipse de demi-axes a et b 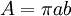
Volume d’une boule de rayon r 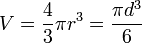
Aire surfacique d’une sphère de rayon r 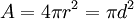
Volume d’un cylindre de hauteur h et de rayon r 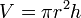
Aire surfacique d’un cylindre de hauteur h et de rayon r 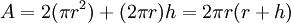
Volume d’un cône de hauteur h et de rayon r 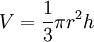
Aire surfacique d’un cône de hauteur h et de rayon r 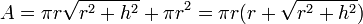
La surface d’un cylindre circonscrit à la sphère et de même hauteur est la même (bases du cylindre exclues).
π se retrouve aussi dans le calcul des surfaces et volumes des hypersphères (à plus de 3 dimensions). La mesure d’angle 180° (en degrés) est égale à π radians.En géométrie non euclidienne, la somme des angles d’un triangle peut être supérieure ou inférieure à π, et le rapport de la circonférence du cercle à son diamètre peut aussi être différent de π.
Définitions alternatives
Article détaillé : Exponentielle.La définition historique et usuelle du nombre π (le rapport de la circonférence d’un cercle et de son diamètre) est parfois gênante pour dégager les propriétés du nombre π, qui dépassent largement le cadre de la géométrie euclidienne. À l’instar des fonctions cosinus et sinus qui sont définies de manière intuitive grâce au cercle trigonométrique mais de manière rigoureuse grâce aux séries entières, nous pouvons introduire une définition analytique de π, ce qui facilite grandement l’étude de ce nombre grâce aux outils de l’analyse.
Les propriétés exp(z+w)=exp(z)exp(w) et exp(0)=1 qui découlent de la définition analytique de l’exponentielle font que l’application
 est un morphisme de groupes continu du groupe
est un morphisme de groupes continu du groupe 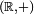 vers le groupe
vers le groupe 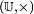 (où
(où 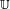 est l’ensemble des complexes de module égal à 1). On démontre alors que l’ensemble des nombres réels t tels que exp(it) = 1 est de la forme
est l’ensemble des complexes de module égal à 1). On démontre alors que l’ensemble des nombres réels t tels que exp(it) = 1 est de la forme 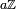 où a est un réel strictement positif. On pose alors π = a / 2. Le calcul intégral permet ensuite de vérifier que cette définition abstraite correspond bien à celle de la géométrie euclidienne.
où a est un réel strictement positif. On pose alors π = a / 2. Le calcul intégral permet ensuite de vérifier que cette définition abstraite correspond bien à celle de la géométrie euclidienne.Le groupe Bourbaki propose une définition alternative très voisine en démontrant l’existence d’un morphisme de groupe f continu de
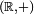 vers
vers 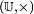 tel que f(1/4) = i. Il démontre que ce morphisme est périodique de période 1, dérivable et qu’il existe un réel a tel que, pour tout réel x, f'(x) = 2iaf(x). Il définit π comme le réel ainsi trouvé.
tel que f(1/4) = i. Il démontre que ce morphisme est périodique de période 1, dérivable et qu’il existe un réel a tel que, pour tout réel x, f'(x) = 2iaf(x). Il définit π comme le réel ainsi trouvé.Les deux méthodes précédentes consistent en réalité à rectifier le cercle soit avec la fonction
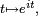 soit avec la fonction
soit avec la fonction 
Mais on peut aussi définir π grâce au calcul intégral en posant :
ce qui revient à calculer l’aire d’un quart de disque
Ou bien à l’aide du dénombrement, en appelant
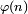 , le nombre de couples d’entiers naturels (k, p) tels que
, le nombre de couples d’entiers naturels (k, p) tels que 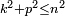 et en définissant :
et en définissant :ce qui est une autre méthode de quarrer le quart de cercle.
Ou bien encore, si la fonction cosinus a été définie formellement soit par sa série entière soit par l’unique solution de l’équation différentielle y'' = − y vérifiant f(0) = 1 et f'(0) = 0, le nombre π peut être défini comme le plus petit réel positif a tel que cos(a)= - 1.
Enfin, toutes les suites établies dans la section suivante fournissent une définition alternative de π.
Suites et séries
De nombreuses suites ou séries convergent vers π ou un multiple rationnel de π et sont même à l’origine de calculs de valeurs approchées de ce nombre.
Méthode d’Archimède
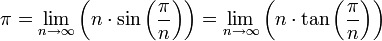 .
.
Les deux suites définies par
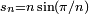 , et
, et 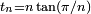 , n ≥ 3, représentent les demi-périmètres des polygones réguliers à n côtés, inscrit dans le cercle trigonométrique pour sn, exinscrit pour tn. On les exploite par des suites extraites dont l’indice (le nombre de côtés du polygone) double à chaque itération, pour obtenir π par passage à la limite d’expressions utilisant les opérations arithmétiques élémentaires et la racine carrée. Ainsi on peut s’inspirer de la méthode utilisée par Archimède — voir historique du calcul de π — pour donner une définition par récurrence des suites extraites de termes
, n ≥ 3, représentent les demi-périmètres des polygones réguliers à n côtés, inscrit dans le cercle trigonométrique pour sn, exinscrit pour tn. On les exploite par des suites extraites dont l’indice (le nombre de côtés du polygone) double à chaque itération, pour obtenir π par passage à la limite d’expressions utilisant les opérations arithmétiques élémentaires et la racine carrée. Ainsi on peut s’inspirer de la méthode utilisée par Archimède — voir historique du calcul de π — pour donner une définition par récurrence des suites extraites de termes 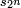 et
et  ou encore
ou encore  et
et 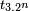 , à l’aide des identités trigonométriques usuelles :
, à l’aide des identités trigonométriques usuelles :En utilisant les identités trigonométriques,
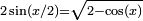 et
et 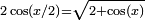 (x ∈ [0,π]), on peut exprimer s2k+1 et s3.2k (k≥1) par emboîtements successifs de racines carrées. On obtient les formules qui suivent pour π.
(x ∈ [0,π]), on peut exprimer s2k+1 et s3.2k (k≥1) par emboîtements successifs de racines carrées. On obtient les formules qui suivent pour π.π peut alors s’exprimer sous la forme d’une formule où s'emboîtent des racines carrées :
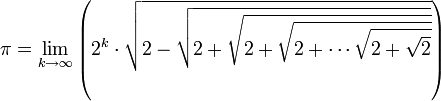 (k est le nombre de racines carrées emboitées)
(k est le nombre de racines carrées emboitées)
ou encore :
Une autre expression de s2k+1, qui peut se déduire simplement de la première de ces deux égalités (multiplier par √(2+√…)), conduit au produit infini suivant (formule de François Viète, 1593).
Sommes et produits infinis
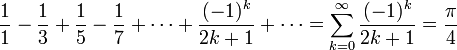 (formule de Leibniz, James Gregory et Madhava de Sangamagrama[8],[10])
(formule de Leibniz, James Gregory et Madhava de Sangamagrama[8],[10])
 (produit de Wallis)
(produit de Wallis)
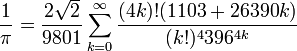 (formule due à Ramanujan)
(formule due à Ramanujan)
 (formule due à David et Gregory Chudnovsky)
(formule due à David et Gregory Chudnovsky)
Fonction zêta de Riemann
Article détaillé : Fonction zêta de Riemann.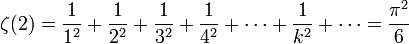 (Euler)
(Euler)
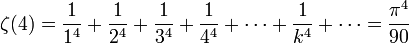 ,
,
- et plus généralement, Euler indiqua que ζ(2n) est un multiple rationnel de π2n pour un entier positif n.
Fonction Gamma d’Euler
Fraction continue
π peut s’écrire sous forme de fractions continues généralisées remarquables :
Les démonstrations ainsi que d’autres représentations sont données dans l’article Fraction continue.
Théorie des nombres
La fréquence d’apparition de paires d’entiers naturels premiers entre eux parmi les paires d’entiers comprises entre 0 et N tend vers 6/π² quand N tend vers l’infini.
Le nombre moyen de façons d’écrire deux entiers positifs quelconques compris entre 0 et N comme la somme de deux carrés parfaits, en tenant compte de l’ordre, tend vers π/4 quand N tend vers l’infini.
 où
où 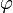 est la fonction indicatrice d'Euler (cf. aussi les suites de Farey).
est la fonction indicatrice d'Euler (cf. aussi les suites de Farey).Probabilité
L’aiguille de Buffon est une expérience de probabilité proposée par Georges-Louis Leclerc, comte de Buffon et consistant à calculer la probabilité qu’une aiguille de longueur a, lancée sur une parquet fait de lattes de largeur l, soit à cheval sur deux lattes, cette probabilité p est :
 Évaluation de π par la méthode de Monte Carlo
Évaluation de π par la méthode de Monte Carlo
La méthode de Monte Carlo est une autre expérience probabiliste consiste à prendre au hasard un point dans un carré de côté 1, la probablité que ce point soit dans le quart de disque de rayon 1 est de π/4.
Les deux formules suivantes, tirées de l’analyse trouvent des applications pratique en probabilité. L’une permet de montrer la convergence de la loi binomiale vers la loi de Gauss et l’autre permet de calculer la densité d’une loi de Gauss.
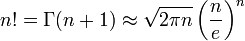 (formule de factorielle de Stirling)
(formule de factorielle de Stirling)
Voir aussi
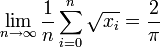 presque sûrement, lorsque les xi sont les itérés de la fonction logistique de paramètre μ = 4 appliquée à un réel x0 choisi dans l'intervalle [0, 1] (c’est-à-dire qu’on définit, pour tout i > 0,
presque sûrement, lorsque les xi sont les itérés de la fonction logistique de paramètre μ = 4 appliquée à un réel x0 choisi dans l'intervalle [0, 1] (c’est-à-dire qu’on définit, pour tout i > 0, 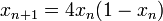 ).
).Autour de π
Retenir π
Un moyen mnémotechnique est ce poème[20] où le nombre de lettres de chaque mot correspond à une décimale, hormis un mot de 10 lettres codé « 0 » :
- Que j’aime à faire apprendre un nombre utile aux sages !
- Immortel Archimède, artiste, ingénieur,
- Qui de ton jugement peut priser la valeur ?
- Pour moi ton problème eut de pareils avantages.
- Jadis, mystérieux, un problème bloquait
- Tout l’admirable procédé, l’œuvre grandiose
- Que Pythagore découvrit aux anciens Grecs.
- Ô quadrature ! Vieux tourment du philosophe
- Insoluble rondeur, trop longtemps vous avez
- Défié Pythagore et ses imitateurs.
- Comment intégrer l’espace plan circulaire ?
- Former un triangle auquel il équivaudra ?
- Nouvelle invention : Archimède inscrira
- Dedans un hexagone ; appréciera son aire
- Fonction du rayon. Pas trop ne s’y tiendra :
- Dédoublera chaque élément antérieur ;
- Toujours de l’orbe calculée[21] approchera ;
- Définira limite ; enfin, l’arc, le limiteur
- De cet inquiétant cercle, ennemi trop rebelle
- Professeur, enseignez son problème avec zèle
En 2005, un Japonais de 59 ans, Akira Haraguchi, a réussi à aligner par cœur 83 431 décimales de π en 13 heures. Il réitéra son record un an plus tard (2006) en mémorisant et récitant publiquement 100 000 décimales pendant 16 heures. Cet exploit a été homologué par le Livre Guinness des records.
Hommages à π
Une tradition anglo-saxonne veut que l’on fête l’anniversaire de π dans certains départements mathématiques des universités le 14 mars. Le 14 mars qui est noté "3/14" en notation anglo-saxonne, est donc appelé la journée de pi[22]. On y mange des tartes (pie en anglais).
De même, le 22 juillet, noté "22/7", est l'occasion de fêter une approximation de π.
Le système logiciel de composition de documents TeX a choisi, en hommage à π, de nommer ses versions du nom des approximations décimales successives de pi. La version actuelle est donc la version 3.1415926
π et culture populaire
Si π est un nombre univers, il est normal, quoique parfois surprenant, de trouver dans les décimales de π, n’importe quelle séquence de nombres. Jean-Paul Delahaye[19] signale par exemple que la somme des 20 premières décimales de π donne 100 ; Robert Gold, amateur de guématrie, affirme avoir trouvé, à l’aide de calculs compliqués, que les mots clefs de la Bible étaient dans π[23].
Nombreux sont les sites ou ouvrages qui signalent la présence du nombre π dans les pyramides et, plus précisément, que π est le rapport entre le périmètre de la base et le double de la hauteur des pyramides[24]. Il est vrai que la pyramide de Khéops possède une pente de 14/11, et que, par conséquent, le rapport entre la base et la hauteur est de 22/14. Le rapport 22/7 étant une bonne approximation de π , le rapport entre le périmètre et le double de la hauteur de la pyramide de Khéops est bien voisin de π . Faut-il pour autant y chercher une intention ? Rien n’est moins sûr[25] puisque la pente des pyramides n’est pas constante et que, selon les régions et les époques, l’on trouve des pentes de 6/5 (pyramide rouge), 4/3 (pyramide de Khephren) ou 7/5 (pyramide rhomboïdale) qui conduisent à un rapport entre périmètre et double de la hauteur éloigné de π.
Notes et références
- ↑ dans un plan euclidien
- ↑ Ce qui a été prouvé par Ferdinand Lindemann en 1882 : Lindemann, F. « Über die Zahl π », Mathematische Annalen 20 (1882), p. 213-225.
- ↑ Tablettes de Suse - voir par exemple ici
- ↑ Voir une traduction du texte original
- ↑ Florian Cajori, A History of Mathematical Notations [détail des éditions] , volume 2, p. 9 nos 396 - 398
- ↑ Karine Chemla, Guo Shuchun, Neuf Chapitres. Le Classique de la Chine ancienne et ses commentaires. Edition critique" [détail des éditions], p. 144-147
- ↑ (en) D’après sa biographie sur le site de Mac Tutor, dans son texte Zhui shu.
- ↑ a et b attribuée souvent à Leibniz, mais découverte probablement antérieurement par Gregory, voir (en)Pi_through_the_ages.html sur le site de l’université de Saint Andrews. Cette formule avait également été trouvée vers 1400 par le mathématicien indien Madhava, mais cette découverte resta inconnue du monde occidental.
- ↑ Voir (en)Squaring the circle, et la (en)biographie de Gregory sur le site de l’université de Saint Andrews
- ↑ a et b (en) Biographie de Madhava sur le site de l’université de Saint-Andrew
- ↑ a et b http://www-history.mcs.st-andrews.ac.uk/HistTopics/Pi_chronology.html
- ↑ 26 décimales suffisent pour estimer la taille de l’univers avec une précision égale à la taille d’un atome.
- ↑ La recherche, no 392, Décembre 2005, L’indispensable nombre π
- ↑ (en)site de bailey
- ↑ Voir (en) page de Simon Plouffe
- ↑ Pour plus de détail voir Fraction continue et approximation diophantienne#Nombre de Pythagore
- ↑ La recherche, no 392, Décembre 2005, L'indispensable nombre π
- ↑ octobre 2008
- ↑ a et b Conférence de Jean-Paul Delahaye, le nombre pi est-il simple ou compliqué consultable ici
- ↑ Publié pour la première fois par the academy, d'après la Revue scientifique, 1905. Les quatre premiers vers sont connus en 1846, dans Le livre des singularites, Gabriel Peignot, G. P. Philomneste
- ↑ Le mot orbe est du masculin mais ce ne fut pas toujours le cas, ceci induit à présent une faute d’accord à « calculée » que l’on peut remplacer par « escompté », par exemple, pour conserver le bon nombre de lettres.
- ↑ (en) Site « officiel » de la journée de pi.
- ↑ Robert Gold, "Dieu et le nombre pi", Éditions O. Bène Kénane, ISBN 9652227277
- ↑ Voir par exemple Le secret de la grande pyramide" de George Barbarin
- ↑ Selon The journal of the Society for the study of Egyptian Antiquities, ISSN 0383-9753, 1978, vol 8, n4, « la valeur de π apparaissant dans la relation entre la hauteur et la longueur de la pyramide est vraisemblablement co-accidentelle »
Annexes
Articles connexes
Bibliographie
- Jean-Paul Delahaye, Le fascinant nombre π, Éditions Belin, Pour la Science - (ISBN 2-9029-1825-9)
- Pierre Eymard, Jean-Pierre Lafon, Autour du nombre Pi, Éditions Hermann, Paris, 1999 - (ISBN 2705614435)
- Jörg Arndt & Christoph Haenel : À la poursuite de π, Éditions Vuibert, 2006 - (ISBN 2-7117-7170-9)
Liens externes
- (fr) La preuve par Lambert de l’irrationalité de π (1761), commentée sur le site BibNum
- (fr) Nombreuses informations historiques et mathématiques sur pi dans pi314.net
- (en) Site permettant une recherche de chiffres dans les 200 000 000 premières décimales
- (en) Le site Wolfram Mathematics compile de nombreuses formules pour π
- Portail des mathématiques
- Portail de la géométrie
Catégories : Nombre transcendant | Constante mathématique | Histoire des mathématiques | Grandeur sans dimension | Pi
Wikimedia Foundation. 2010.






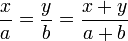

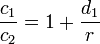
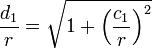



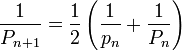
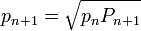
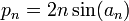
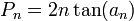
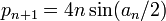
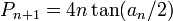
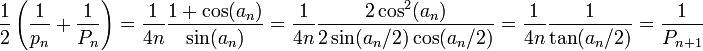

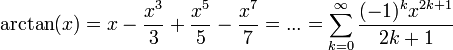
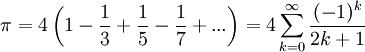

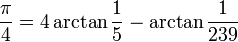

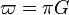
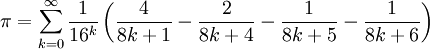


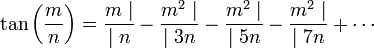

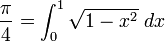
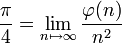
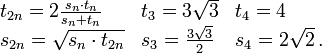
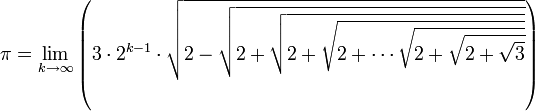
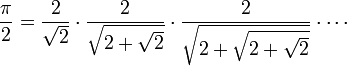
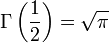 (
(
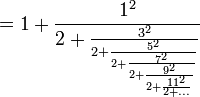 (
(