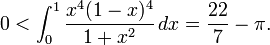- 22 / 7 dépasse π
-
22 / 7 dépasse π
Les preuves du célèbre résultat mathématique que le nombre rationnel 22 / 7 est supérieur à π remontent à l'Antiquité. Ce qui suit est une démonstration mathématique moderne que 22 / 7> π, nécessitant uniquement des techniques élémentaires de calcul. Le but n'est pas d'abord de convaincre le lecteur que 22 / 7 est en effet plus grand que π; des méthodes de calcul systématiques de la valeur de π existent. Contrairement à certaines preuves élémentaires, le calcul fondé sur la preuve présentée ici est simple, son élégance résultant de ses liens avec la théorie des approximations diophantines. Stephen Lucas qualifie cette proposition de "l'un des plus beaux résultats liés à l'approximation de π". Julian Havil met fin à une discussion sur les fractions approchant π avec ce résultat, le décrivant comme "impossible de ne pas être mentionné" dans ce contexte.
Les détails
Il reste de démontrer que l'intégral en effet evalue à la quantité désirée:
-
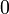
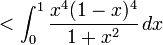
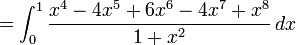
(développer les termes du numérateur) 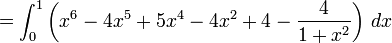
(faire la division polymomiale, un aspect important de la formulation de la géométrie algébrique) 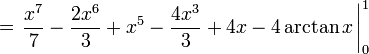
(integration définie) 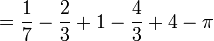
(substituer un pour x, puis zéro pour x, et faire soustraire l'un de l'autre, utiliser arctan(1) = π/4) 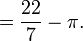
(addition)
- Portail des mathématiques
Catégories : Analyse | Algèbre | Pi | Approximation diophantienne
Wikimedia Foundation. 2010.