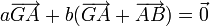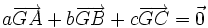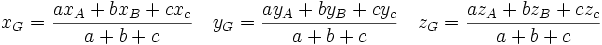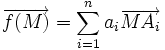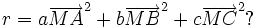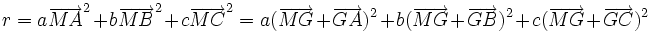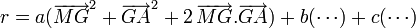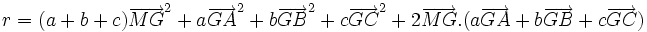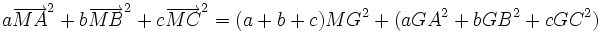- Barycentre (mathématiques élémentaires)
-
Barycentre (géométrie euclidienne)
 Pour les articles homonymes, voir Barycentre.
Pour les articles homonymes, voir Barycentre.En géométrie, le barycentre est un point qui permet de résumer un ensemble géométrique sur lequel sont réparties des valeurs numériques. Ces valeurs peuvent représenter des poids pour déterminer le point d'équilibre d'un mobile. Mais le barycentre permet aussi de caractériser le centre d'inertie d'un solide ou concentrer un ensemble de charges électriques.
Mathématiquement, le barycentre s'obtient en annulant une relation vectorielle. Cette notion généralise la construction du milieu d'un segment ou du centre de gravité d'un triangle.
Sommaire
Barycentre de deux points
Point d'équilibre
Le terme de barycentre est formé sur la racine grecque barus (lourd) pour désigner un centre des poids ou centre d'équilibre. Sa conception est liée au théorème des moments découvert par Archimède au IIIe siècle av. J.-C.
Pour que la balance soit en équilibre, il faut que les moments, c'est-à-dire les produits des longueurs de bras par les masses correspondantes, soient égaux. Autrement dit le point d'équilibre est caractérisé par la relation :
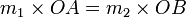 .
.Par exemple, si la masse m1 est 4 fois plus importante que la masse m2, il faudra que la longueur OA soit 4 fois plus petite que la longueur OB.
Ce principe des moments est d'ailleurs utilisé dans la balance dite romaine
Les poids peuvent également avoir une valeur numérique négative, si l'une des masses est remplacée par un ballon d'hélium, par exemple. Dans ce cas, le point d'équilibre se situe en dehors de l'espace délimité par les deux objets.
Relation vectorielle
En géométrie affine, le point d'équilibre, ou barycentre, est noté G et les poids des points fixes A et B sont notés usuellement a et b. Le théorème des moments est remplacé par la relation
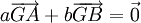 .
.
À l'aide de la relation de Chasles, cette relation peut se réécrire sous la forme
c'est-à-dire
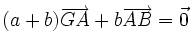 ou de manière équivalente
ou de manière équivalente 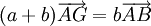 .
.Si la somme a + b est non nulle, il existe un unique point G qui satisfait cette relation, donné par la relation
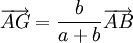 .
.Colinéarité
De la définition
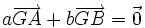 , on tire que
, on tire que 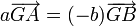 ou encore que
ou encore que 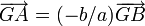 ; ainsi
; ainsi 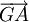 et
et 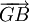 sont colinéaires et ont un point en commun, G. Par conséquent, G appartient à la droite (AB). Nous venons de démontrer que
sont colinéaires et ont un point en commun, G. Par conséquent, G appartient à la droite (AB). Nous venons de démontrer que- si G est le barycentre de {(A,a),(B,b)} alors G appartient à la droite (AB).
Si G est sur le segment [AB] (entre A et B) alors
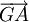 et
et 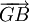 sont de sens opposé, ce qui se traduit par
sont de sens opposé, ce qui se traduit par 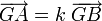 avec k< 0. Mais, comme dans le même temps
avec k< 0. Mais, comme dans le même temps 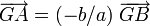 , on en déduit que b et a sont de même signe. Nous venons de démontrer que
, on en déduit que b et a sont de même signe. Nous venons de démontrer que- Si G est sur le segment [AB] (entre A et B) alors a et b sont de même signe.
Coordonnées barycentriques
On démontre (à démontrer ultérieurement) que, si A et B sont distincts, tout point M de la droite (AB) peut s'écrire comme barycentre des points A et B. Les pondérations obtenues sont appelées les coordonnées barycentriques du point M.
Homogénéité
Si G est le barycentre de {(A,a);(B,b)} alors,
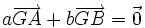 , et il vient que pour tout réel k
, et il vient que pour tout réel k 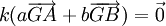 . Autrement dit, on obtient
. Autrement dit, on obtient 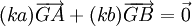 De plus, comme a + b est non nul, pour tout k réel non nul, k(a + b) est également non nul. Alors G est le barycentre de {(A,k.a);(B,k.b)}.
De plus, comme a + b est non nul, pour tout k réel non nul, k(a + b) est également non nul. Alors G est le barycentre de {(A,k.a);(B,k.b)}.Nous venons de démontrer que
- si G est le barycentre de {(A,a);(B,b)} alors pour tout k réel non nul, G est aussi le barycentre de {(A,ka);(B,kb)}.
Cette propriété s'appelle l'homogénéité.
Réduction
L'application de la relation de Chasles à
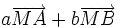 , en introduisant le barycentre G de (A,a),(B,b) donne
, en introduisant le barycentre G de (A,a),(B,b) donne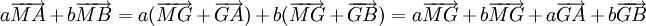 .
.G étant barycentre de (A,a),(B,b) alors
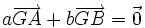 . La relation précédente devient:
. La relation précédente devient: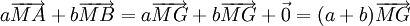 .
.
Nous venons de démontrer que
- si G est le barycentre de (A,a),(B,b) alors pour tout M du plan,
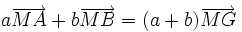 .
.
C'est la propriété de réduction.
Elle permet de positionner le point G par rapport à tout point M. Si M est l'origine d'un repère du plan ou de l'espace, elle permet de définir les coordonnées du point G
Barycentre de trois points dans le plan ou dans l'espace
La définition peut se généraliser à trois points : pour tous réels a, b et c tels que a + b + c soit non nul, il existe un unique point G tel que
appelé barycentre du système pondéré {(A,a);(B,b);(C,c)}. Les points G, A, B et C sont toujours coplanaires et on démontre que , si A, B, C définissent un plan, tous les points M de ce plan peuvent s'écrire comme barycentre de A, B et C. Les pondérations s'appellent alors coordonnées barycentriques de M dans le repère A, B et C
Comme pour le barycentre de deux points, le barycentre de trois points permet de réduire l'expression vectorielle
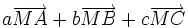 , pour tout point M :
, pour tout point M :Ce qui permet, en remplaçant M par l'origine du repère, de donner les coordonnées du point G
Ce barycentre possède en outre une propriété dite d'associativité ou de barycentre partiel : si a + b est non nul et si G1 est le barycentre du système {(A,a);(B,b)}, alors G est le barycentre du système {(G1,a + b);(C,c)}. Cela signifie que la construction du barycentre de trois points peut se ramener à la construction de barycentres de deux points.
Cette propriété simplifie grandement les problèmes d'alignement et de concours.
En considérant ces trois points comme les sommets d’un triangle, le centre de gravité est le point d'intersection de ses 3 médianes. Le centre de gravité est situé aux
 d'une médiane en partant du sommet.
d'une médiane en partant du sommet.
Autrement dit, soit un triangle ABC, A' le milieu de [BC], B' le milieu de [AC], et C' le milieu de [AB] et G son centre de gravité.
Alors : 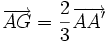 ,
, 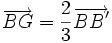 et
et 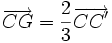 .
.Le centre de gravité est aussi l' isobarycentre des sommets du triangle, c'est-à-dire que
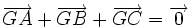 .
.Barycentre de n points
On peut généraliser la définition à n points dans un espace affine E quelconque. On définit alors une fonction f de E dans
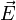 , appelée fonction vectorielle de Leibniz :
, appelée fonction vectorielle de Leibniz :On démontre que si
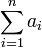 est non nul, la fonction s'annule pour un unique point G appelé barycentre du système {(Ai,ai)}i = 1...n. Ce point G est toujours dans le sous-espace affine engendré par les (Ai). Réciproquement, si les Ai constituent une famille libre de n points d'un sous-espace affine F de dimension n - 1, tout point M de F peut s'écrire comme barycentre des points (Ai). Les pondérations s'appellent les coordonnées barycentriques de G dans le repère (Ai).
est non nul, la fonction s'annule pour un unique point G appelé barycentre du système {(Ai,ai)}i = 1...n. Ce point G est toujours dans le sous-espace affine engendré par les (Ai). Réciproquement, si les Ai constituent une famille libre de n points d'un sous-espace affine F de dimension n - 1, tout point M de F peut s'écrire comme barycentre des points (Ai). Les pondérations s'appellent les coordonnées barycentriques de G dans le repère (Ai).Réduction de fonctions vectorielles ou du second degré
Article détaillé : Fonctions de Leibniz.À partir du barycentre, il est possible de réduire des expressions vectorielles. Prenons l'exemple de 3 points seulement A B C de poids a b c et leur barycentre G. La formule du premier degré est celle du barycentre :
 qui permet de nombreux calculs du premier degré sur les vecteurs.
qui permet de nombreux calculs du premier degré sur les vecteurs.
A partir du barycentre il est possible de définir une formule du second degré, au sens du produit scalaire des vecteurs : Que peut-on dire de la formule du second degré suivante, dont le résultat est un nombre r
Remplaçons chaque vecteur
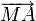 etc par
etc par  et appliquons la formule du carré d'une somme:
et appliquons la formule du carré d'une somme:Les doubles produits s'annulent, d'où le résultat
au second degré où seul le terme MG2 est variable.
Rappelons la formule de départ du premier degré
Exemple pratique
Article détaillé : Théorème de Ceva.Dans le dessin ci-contre (figure 2), les graduations sur chaque côté sont régulières. Les droites (AM) (BN) et (CP) sont concourantes.
- Démonstration
La lecture du dessin permet de dire que
- P est barycentre du système {(A ; 2), (B ; 1)}
- N est barycentre du système {(A ; 3), (C ; 1)}
- M est barycentre du système {(B ; 3), (C ; 2)}
La propriété d'homogénéité du barycentre permet de dire que
- P est barycentre du système {(A ; 6), (B ; 3)}
- N est barycentre du système {(A ; 6), (C ; 2)}
- M est barycentre du système {(B ; 3), (C ; 2)}
Il suffit alors de créer un point G barycentre du système {(A ; 6) , (B ; 3) ; (C ; 2)} et d'utiliser trois fois la propriété d'associativité
- G est barycentre du système {(P ; 9), (C ; 2)} donc G est sur la droite (PC)
- G est barycentre du système {(N ; 8), (B ; 3)} donc G est sur la droite (NB)
- G est barycentre du système {(M ; 5), (A ; 6)} donc G est sur la droite (AM)
G est donc le point de concours des trois droites.
Voir aussi
- Portail de la géométrie
Catégorie : Géométrie euclidienne
Wikimedia Foundation. 2010.