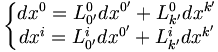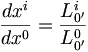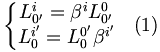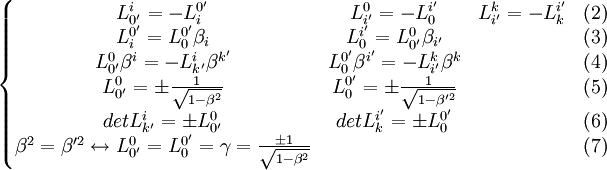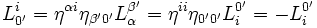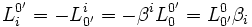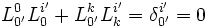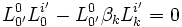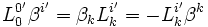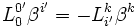- Transformations de Lorentz
-
Transformation de Lorentz
- Cet article présente les transformations de Lorentz sous un aspect technique. Le lecteur désireux d'obtenir des informations physiques plus générales à ce sujet pourra se référer à l'article relativité restreinte.
Les transformations de Lorentz sont des transformations linéaires des coordonnées d'un point dans l'espace-temps de Minkowski, à quatre dimensions (trois d'espace et une de temps) et relativiste. On peut noter que la terminologie subit quelques variations : suivant que la théorie dans laquelle on travaille a trait ou non à la physique quantique, les termes « transformations de Lorentz » désignent des transformations qui peuvent être différentes.
Dans le cadre de la relativité restreinte, les transformations de Lorentz correspondent à la loi de changement de référentiel galiléen, sous laquelle les équations de la physique doivent être préservées, ainsi que la vitesse de la lumière, qui est la même dans tout référentiel galiléen. C'est en particulier pour faire en sorte que les équations de Maxwell s'écrivent à l'identique dans tout référentiel galiléen que Hendrik Antoon Lorentz a introduit mathématiquement cette loi avant qu' Albert Einstein n'en réalise toute la portée physique. L'ensemble de ces transformations des coordonnées, aussi appelées transformations de Lorentz propres et orthochrones, est composé des transformations spécifiques à la relativité restreinte et des rotations dans l'espace à trois dimensions.
Dans le cadre de la physique quantique relativiste, comme en Théorie quantique des champs, ce sont les transformations linéaires de l'espace-temps qui laissent les lois invariantes (en l'absence de charge électrique), ce qui englobe les précédentes et en amène d'autres (la symétrie T et la parité) pour former le groupe de Lorentz.
- En physique la symétrie T et la parité sont interprétées comme des changements de convention d'orientation des axes et ne sont pas utiles en relativité restreinte.
Dans chacun des deux cas l'ensemble des transformations désignées forme un sous-groupe du groupe de Poincaré.
Sommaire
Les formules
On ramène le problème à deux dimensions pour plus de lisibilité, donc on néglige les détails sur les rotations spatiales.
En relativité restreinte :
- En considérant deux référentiels
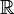 et
et 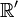 en translation rectiligne uniforme l'un par rapport à l'autre à la vitesse
en translation rectiligne uniforme l'un par rapport à l'autre à la vitesse 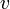 parallèle à l'axe des x, les transformations de Lorentz utilisées sont :
parallèle à l'axe des x, les transformations de Lorentz utilisées sont :
-
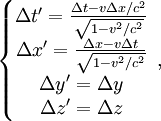 en posant
en posant 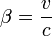 et
et 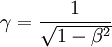 , on écrit :
, on écrit : 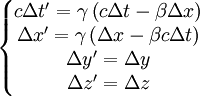
En physique quantique relativiste :
- Les transformations de Lorentz qui doivent laisser invariantes les équations (en l'absence de charge électrique) sont :
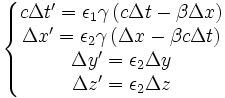 avec
avec 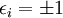 indiquent s'il y a un changement d'orientation temporelle et/ou spatiale.
indiquent s'il y a un changement d'orientation temporelle et/ou spatiale.
- En considérant l'inversion temporelle T et l'inversion spatiale P, toute transformation utilisée en physique quantique est de la forme
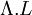 , avec
, avec 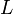 une transformation de Lorentz de la relativité restreinte (orthochrone et propre) et
une transformation de Lorentz de la relativité restreinte (orthochrone et propre) et 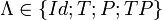 .
.
Le groupe des transformations propres et orthochrones étant connexe, la décomposition ci-dessus permet de voir que le groupe de Lorentz est formé de quatre composantes connexes, et que le groupe des transformations spéciales (i.e : de déterminant positif) est composé de deux composantes connexes.
Limites non relativistes
Groupe de Galilée
Les formules du groupes de Lorentz peuvent s'approximer dans le cas où la vitesse
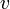 du corps est petite devant celle de la lumière, ou, ce qui revient au même, en faisant tendre la vitesse de la lumière
du corps est petite devant celle de la lumière, ou, ce qui revient au même, en faisant tendre la vitesse de la lumière  vers l'infini. En négligeant le terme
vers l'infini. En négligeant le terme 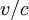 dans les formules, on retrouve alors le groupe de Galilée qui est le groupe des transformations correspondantes aux changements de référentiel en physique classique.
dans les formules, on retrouve alors le groupe de Galilée qui est le groupe des transformations correspondantes aux changements de référentiel en physique classique.Groupe de Carrol
Le groupe de Carrol est une autre approximation non relativiste des éléments du groupe de Lorentz dans le cas où on s'intéresse aux intervalles grands de genre espace. Cette approximation, découverte par Jean-Marc Lévy-Leblond en 1965, n'a d'intéret que pédagogique, d'après son découvreur.[1]
Différentes méthodes pour trouver les transformations
- Pour la relativité restreinte, Einstein a initié une méthode[2] :
- À partir du principe de relativité et de l'invariance de la vitesse de la lumière par changement de référentiel, de l'homogénéité et de l'isotropie supposées de l'espace, et à l'aide d'une représentation géométrique d'une situation idéale où deux référentiels inertiels permettent de voir, mesurer les longueurs, et chronométrer le temps d'un référentiel à l'autre, on démontre les différentes formules par un système d'équations linéaires dont il faut trouver les coefficients. Les transformations non physiques sont parfois écartées sans détail par le choix de la solution positive dans une équation du second degré, choix dû à l'hypothèse physique de l'orientation des repères par une règle telle que celle de la main droite, illustrée par la représentation géométrique accompagnant le raisonnement[3].
- En physique quantique relativiste, comme en Théorie quantique des champs, les transformations utilisées sont définies comme les symétries de l'espace de Minkowski qui laissent inchangées les équations (en l'absence de charge électrique). Cela revient à déterminer les transformations linéaires laissant inchangé l'intervalle d'espace-temps : c'est une définition mathématique pour laquelle les changements de référentiel pour des observateurs ne sont que certaines de ces transformations et qui permet de les trouver toutes.
Cette méthode est aussi utilisée dans certains manuels de relativité restreinte, après avoir démontré que l'invariance de l'intervalle d'espace-temps par changement de référentiel découle directement des deux axiomes de la relativité restreinte, et en éliminant les transformations qui ne respectent pas la convention d'orientation pour les repères tridimensionnels (règle de la main droite, en général) et d'orientation de l'axe du temps vers le futur ; élimination faite de diverses manières, parfois marquées du sceau de l'évidence[4], et parfois plus justifiées[5].
La méthode géométrique
On suppose que l'espace-temps physique est un espace affine où les référentiels sont identifiés aux repères de cet espace affine. De plus on néglige les translations constantes entre les repères qui ne se manifestent que par des additions de nombres constants aux coordonnées. Donc, la transformation des coordonnées s'effectue au moyen d'un opérateur linéaire :
Soient deux référentiels
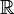 et
et 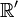 en translation rectiligne l'un par rapport à l'autre sur des axes parallèles, avec une vitesse relative v selon l'axe Ox. Soient
en translation rectiligne l'un par rapport à l'autre sur des axes parallèles, avec une vitesse relative v selon l'axe Ox. Soient 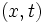 les coordonnées spatio-temporelles d'un événement dans le référentiel
les coordonnées spatio-temporelles d'un événement dans le référentiel 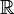 , et
, et 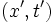 ses coordonnées dans le référentiel
ses coordonnées dans le référentiel 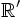 . (Pour simplifier les notations, on ne tiendra pas compte dans ce paragraphe des deux autres composantes spatiales y et z).
. (Pour simplifier les notations, on ne tiendra pas compte dans ce paragraphe des deux autres composantes spatiales y et z).- Utilisation du principe de relativité :
- Par le principe de relativité, les coefficients de la transformation linéaire ne dépendent que de la vitesse relative entre les référentiels, et d'aucune considération extérieure à ces deux référentiels. Pour plus de précision, on devrait dire des vitesses relatives des référentiels, le sujet est abordé un peu plus loin.
- Première utilisation de la vitesse de la lumière :
- Si dans le référentiel
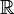 on considère le déplacement d'un signal lumineux dans le sens des x positifs, donc à la vitesse de la lumière, alors
on considère le déplacement d'un signal lumineux dans le sens des x positifs, donc à la vitesse de la lumière, alors 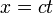 . Mais comme cette vitesse est la même dans le référentiel
. Mais comme cette vitesse est la même dans le référentiel 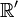 , en considérant le déplacement de ce même signal vu depuis ce référentiel, comme l'axe des x' a la même orientation que celui des x, et de même pour les axes temporels, on doit avoir
, en considérant le déplacement de ce même signal vu depuis ce référentiel, comme l'axe des x' a la même orientation que celui des x, et de même pour les axes temporels, on doit avoir 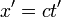 [6]. De même, en commençant par considérer le signal depuis
[6]. De même, en commençant par considérer le signal depuis 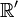 .
.
- Donc :
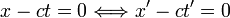
- Et comme x, t, x', t' sont liés par des relations linéaires à coefficients constants, on doit avoir
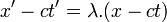 pour un certain λ constant.
pour un certain λ constant.
- Deuxième utilisation de la vitesse de la lumière :
- En considérant le déplacement d'un signal lumineux dans le sens des x négatifs, et en faisant le même raisonnement, on obtient :
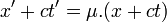 pour un certain μ constant.
pour un certain μ constant.
- Conclusion sur la vitesse de la lumière :
- En additionnant et soustrayant les deux égalités précédentes, on obtient :
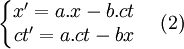
- avec :
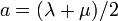 et
et 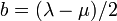 .
.
- Première utilisation de la vitesse relative des référentiels :
- Pour l'origine du référentiel
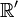 , on a x' = 0 et donc, d'après la première équation du système (2), on a :
, on a x' = 0 et donc, d'après la première équation du système (2), on a : 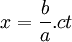
- En désignant par
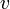 la vitesse du référentiel
la vitesse du référentiel 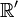 par rapport au référentiel
par rapport au référentiel 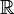 , on peut donc écrire
, on peut donc écrire 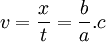 , ou
, ou 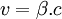 , avec
, avec 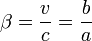
- On peut donc écrire :
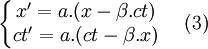
- Deuxième utilisation de la vitesse relative des référentiels :
- Pour l'origine du référentiel
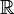 , on a x = 0 et donc, d'après les équations du système (2), on a :
, on a x = 0 et donc, d'après les équations du système (2), on a : 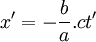
- En désignant par
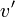 la vitesse du référentiel
la vitesse du référentiel 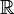 par rapport au référentiel
par rapport au référentiel 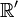 , on peut donc écrire
, on peut donc écrire 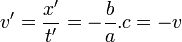 .
.
- Utilisation des hypothèses sur l'espace :
- Quand t = 0, on a
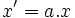 . Le coefficient a permet donc de convertir la mesure d'une longueur faite dans le référentiel
. Le coefficient a permet donc de convertir la mesure d'une longueur faite dans le référentiel 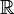 , en la mesure faite dans
, en la mesure faite dans 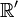 . Ce coefficient peut dépendre de la vitesse relative
. Ce coefficient peut dépendre de la vitesse relative 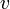 entre les référentiels, mais pas de sa direction ni de son sens par l'hypothèse de l'isotropie de l'espace. De plus, comme expliqué en début de paragraphe, a est indépendant des coordonnées x, t, x', t'.
entre les référentiels, mais pas de sa direction ni de son sens par l'hypothèse de l'isotropie de l'espace. De plus, comme expliqué en début de paragraphe, a est indépendant des coordonnées x, t, x', t'. - Donc a dépend de la norme de la vitesse
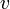 , c'est à dire de
, c'est à dire de 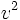 .
.
- Utilisation du principe de relativité :
- En inversant les rôles des référentiels
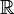 et
et 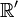 , et ayant justifié que v' = − v, et que
, et ayant justifié que v' = − v, et que 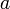 ne dépend pas de la direction ni du sens de
ne dépend pas de la direction ni du sens de 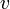 , donc
, donc 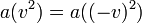 , et on peut écrire :
, et on peut écrire : 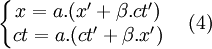
- En utilisant les deux équations du système (3) dans la première équation du système (4), on obtient
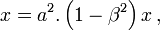 soit :
soit : 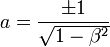
- Le signe + est choisi, sinon il y a changement dans d'orientation entre l'axe des x et l'axe des x', ce qui n'est pas le cas par hypothèse.
- Conclusion :
- Les transformations de Lorentz s'écrivent :
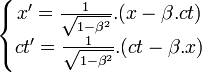
- Ce que l'on écrit souvent :
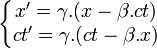
- Avec
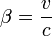 et
et 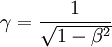 .
.
On trouvera une variante de cette démonstration où les principes de base (référentiels galiléens, vitesse de la lumière indépendante de celle de la source et principe de relativité) sont séparés sur Wikiversité
La méthode partant de l'invariance de la pseudo-norme
Les transformations de Galilée conservent le produit scalaire : :
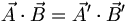
- Dans l'espace-temps de Minkowski, le tenseur métrique est :
![\eta_{\alpha\beta}=\left[\begin{matrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{matrix}\right]](/pictures/frwiki/48/004c15717506cc50bd7be014733e16f5.png)
- Ce qui veut dire que l'on doit différencier les coordonnées covariantes, des coordonnées contravariantes. On définit la pseudo-norme : :ds2 = ηαβdxαdxβ = dxαdxα = c2dt2 − dx2 − dy2 − dz2
- Les transformations de Lorentz doivent conserver la pseudo-norme : :dxαdxα = dx'αdx'α
Les transformations de Lorentz doivent être linéaire à coefficients constants. Dans toute la suite, les indices primés correspondent aux coordonnées dans le référentiel
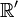 , de plus les répétitions de lettres grecques voudront dire sommation de 0 à 3, et les répétitions de lettres latines de 1 à 3.
, de plus les répétitions de lettres grecques voudront dire sommation de 0 à 3, et les répétitions de lettres latines de 1 à 3.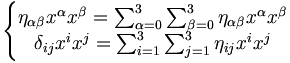
- Les transformations s'écrivent sous la forme matricielle :
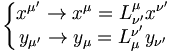
Les pseudo-produits scalaires sont invariants pas transformations de Lorentz :
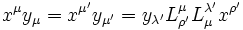 soit donc :
soit donc : 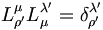 où
où 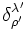 est le symbole de Kronecker. L'inverse de la matrice
est le symbole de Kronecker. L'inverse de la matrice 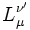 est sa transposée :
est sa transposée : 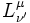 La transformation du tenseur métrique se retrouve en ayant à l'esprit l'invariance du pseudo-produit scalaire :
La transformation du tenseur métrique se retrouve en ayant à l'esprit l'invariance du pseudo-produit scalaire :- xμxμ = xλ'xλ'
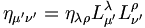
On en déduit que (detL)2 = 1 donc detL = 1 ou detL = − 1.
Terminologie : les transformations vérifiant
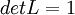 sont appélées les transformations propres, elles forment un groupe appelé le groupe des Transformations Spéciales de Lorentz. Ce groupe a deux composantes connexes. Les autres transformations sont qualifiées d'impropres et ne forment pas un groupe.
sont appélées les transformations propres, elles forment un groupe appelé le groupe des Transformations Spéciales de Lorentz. Ce groupe a deux composantes connexes. Les autres transformations sont qualifiées d'impropres et ne forment pas un groupe.Les transformations s'écrivent alors :
On considère un corps au repos dans le repère
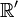 , alors dx'k = 0, d'où :
, alors dx'k = 0, d'où :soit :
Ensuite il y a ces relations à démontrer :
Pour les expressions (2), il suffit d'utiliser la relation :
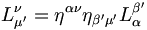 avec ν = i, μ = 0 et μ' = ν' = 0' soit :
avec ν = i, μ = 0 et μ' = ν' = 0' soit :Pour les expressions (3) :
Pour les expressions (4), nous partons de
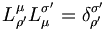 , avec ρ' = 0' et σ' = i'
, avec ρ' = 0' et σ' = i'Pour les expressions (5) les relations de transformations du tenseur métrique donnent :
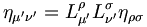 , en prenant μ' = ν' = 0'
, en prenant μ' = ν' = 0'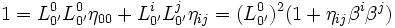
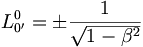
Pour les expressions (6) :
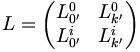 avec
avec 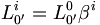 et
et 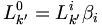 en remarquant :
en remarquant : 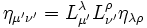 pour μ' = i' et ν' = j' on obtient :
pour μ' = i' et ν' = j' on obtient :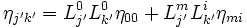
- or :
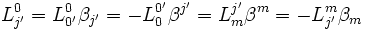
d'où :
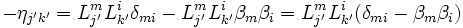
- On prend le déterminant :
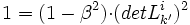
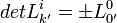
Pour les expressions (7) : Nous avons L' = L − 1 (matrices orthogonales), on a donc :
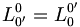 , on a donc β2 = β'2.
, on a donc β2 = β'2.
En se plaçant dans le cadre de la relativité restreinte, les transformations de Lorentz représentent des changements de référentiels :- Il faut appliquer le principe de non retournement du temps, et donc écarter les valeurs négatives pour
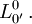 On obtient alors :
On obtient alors : 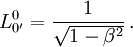 Les transformation de Lorentz alors utilisées sont dites orthochrones.
Les transformation de Lorentz alors utilisées sont dites orthochrones. - Il faut appliquer le principe de non retournement de l'orientation spatiale (par la main droite en général), et donc écarter les cas où
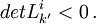 On obtient alors :
On obtient alors : 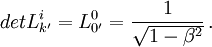 Avec cette condition supplémentaire, les transformations de Lorentz utilisées sont de déterminant égal à 1 : elles sont dites propres.
Avec cette condition supplémentaire, les transformations de Lorentz utilisées sont de déterminant égal à 1 : elles sont dites propres.
Ainsi, les transformations de Lorentz utilisées en relativité restreinte sont celles qui sont propres et orthochrones.
Notes et références
- ↑ Le groupe de Carrol par JM Levi-Leblond, Annales de l'IHP, 1965.
- ↑ Que l'on peut trouver dans La théorie de la relativité, par Albert Einstein, Gauthier-Villard éditeur, 1921, traduit par Mlle J. Rouvrière.
- ↑ Un exemple récent est dans le chapitre 5 du livre Introduction à la relativité par James H.Smith (Masson éditeur, traduit par Philippe Brenier, préfacé par Jean-Marc Levy-Leblond, réédité en 1997, ISBN 2-225-82985-3).
- ↑ Un exemple est dans le §19 du livre Électromagnétisme et gravitation relativistes de Jean-Claude Boudenot (ellipses éditeur, 1989, ISBN 2-7298-8936-1); un autre est dans le Tome 2, §4, de Lev Landau et Evguéni Lifchitz, Physique théorique, éd. MIR, Moscou [détail des éditions].
- ↑ On peut citer (en)Geometrical physics in Minkowski spacetime par E.G. Peter Rowe, Springer-Verlag éditeur ISBN 1852333669 , 2001; (en)The geometry of Minkowski Spacetime par Gregory L. Naber, Springer-Verlag ISBN 3540978488, 1992, où au chapitre 1, §1.3, la conservation des orientations spatiale et temporelle est présentée comme la raison de cette sélection ; ainsi que le livre de Phillipe Tourrenc, Relativité et gravitation (Armand Colin éditeur, ISBN 2-200-21209-7), aux pages 23 à 25, où l'auteur justifie, par l'utilisation du Principe de correspondance, le choix des transformations de Lorentz pour la relativité restreinte parmi toutes les transformations déduites de l'hypothèse de l'invariance de l'intervalle d'espace-temps.
- ↑ Cette égalité n'est valable qu'avec l'hypothèse de conservation des orientations de l'espace et du temps par changement de référentiel. En toute généralité, on doit donc écrire
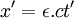 , où
, où 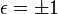 indique l'orientation relative des référentiels (O,x,t) et (O,x',t') et permet d'enrichir la fin du paragraphe d'une discussion sur les choix entre les différentes transformations de Lorentz compatibles avec les mathématiques de la relativité restreinte, en introduisant explicitement l'hypothèse de non-changement de l'orientation des référentiels.
indique l'orientation relative des référentiels (O,x,t) et (O,x',t') et permet d'enrichir la fin du paragraphe d'une discussion sur les choix entre les différentes transformations de Lorentz compatibles avec les mathématiques de la relativité restreinte, en introduisant explicitement l'hypothèse de non-changement de l'orientation des référentiels.
Voir aussi
- Hendrik Antoon Lorentz
- Relativité restreinte
- Relativité générale
- Calculs relativistes
- Covariance
- Invariance de Lorentz
Liens externes
- (en) One more derivation of the Lorentz transformation, Jean-Marc Lévy-Leblond.
- (fr) Les relativités, Jean-Marc Lévy-Leblond, Les Cahiers de Fontenay (n°8).
- (en)Derivation of the Lorentz Transformation par Victor Yakovenko, de l'université du Maryland.
- Portail de la physique
Catégories : Méthode mathématique de la physique | Relativité
Wikimedia Foundation. 2010.