Théorie du Chaos

Théorie du chaos

Pour les articles homonymes, voir Chaos.

Attracteur étrange de Lorenz

La théorie du chaos traite des systèmes dynamiques rigoureusement déterministes, mais qui présentent un phénomène fondamental d'instabilité appelé « sensibilité aux conditions initiales » qui, modulant une propriété supplémentaire de récurrence, les rend non prédictibles en pratique sur le « long » terme.

Introduction

Définition heuristique d'un système chaotique

Un système dynamique est dit chaotique si une portion « significative » de son espace des phases présente simultanément les deux caractéristiques suivantes :

• le phénomène de sensibilité aux conditions initiales.

• une forte récurrence.

La présence de ces deux propriétés entraîne un comportement extrêmement désordonné qualifié à juste titre de « chaotique ». Les systèmes chaotiques s'opposent notamment aux systèmes intégrables de la mécanique classique, qui furent longtemps les symboles d'une régularité toute puissante en physique théorique. La dynamique quasi-périodique d'un système intégrable semblait elle-même trouver son illustration parfaite dans les majestueux mouvements des planètes du système solaire autour du Soleil ; souvenons-nous que Voltaire, qui incita Émilie du Châtelet à entreprendre la traduction des Principia Mathematica de Newton, parlait de Dieu comme du « Grand Horloger »…

Qu'est-ce que la « théorie du chaos » ?

Au cours de son histoire, la physique théorique s'était déjà trouvée confrontée à la description de systèmes complexes macroscopiques, comme un volume de gaz ou de liquide, mais la difficulté à décrire de tels systèmes semblait découler du très grand nombre de degrés de liberté internes du système à l'échelle microscopique (atomes, molécules). La mécanique statistique avait dans ce cas permis de rendre compte de façon satisfaisante des propriétés macroscopiques de ces systèmes à l'équilibre. Ce fut donc une grande surprise lorsqu'on s'aperçut à la fin du XIX^e siècle qu'une dynamique d'une grande complexité pouvait résulter d'un système simple possédant un très petit nombre de degrés de liberté^[1], pourvu qu'il possède cette propriété de sensibilité aux conditions initiales.

La théorie du chaos s'attache principalement à la description de ces systèmes à petit nombre de degrés de liberté, souvent très simples à définir, mais dont la dynamique nous apparaît comme très désordonnée^[2].

La théorie du chaos est-elle née dans les années 1970 ?

Attracteur étrange de Lorenz (1963)

La réponse à cette question est : oui ET non.

• Non, car le phénomène de sensibilité aux conditions initiales a été découvert dès la fin du XIX^e siècle par Henri Poincaré dans des travaux concernant le problème à N corps en mécanique céleste, puis par Hadamard avec un modèle mathématique abstrait aujourd'hui baptisé « flot géodésique sur une surface à courbure négative ». Cette découverte a entraîné un grand nombre de travaux importants, principalement dans le domaine des mathématiques. Ces travaux sont évoqués dans le paragraphe Développements historiques situé plus loin.

• Oui, car ce n'est véritablement que dans les années 1970 que la théorie du chaos s'est progressivement imposée sur le devant de la scène scientifique, opérant une rupture épistémologique forte. Le terme suggestif de « chaos » n'a d'ailleurs été introduit qu'en 1975 par les deux mathématiciens Tien-Yien Li et James A. Yorke^[3]. Le caractère tardif de ce changement de paradigme s'explique aisément : la théorie du chaos doit en effet sa popularisation aux progrès fulgurants de l'informatique à partir des années 1960-70. Cette science nouvelle a en effet rendu accessible aux non-mathématiciens la visualisation directe de l'incroyable complexité de ces systèmes dynamiques, auparavant réservée aux seuls « initiés » capables d'absorber le formalisme mathématique idoine.

À titre d'illustration, la figure ci-contre est un exemple typique d'images produites par la théorie du chaos ; il s'agit ici d'un objet géométrique découvert par Lorenz en 1963, et baptisé depuis « attracteur étrange ». (Cet objet sera commenté plus bas, au paragraphe : Lorenz & la météorologie.)

La théorie du chaos est une véritable théorie scientifique, qui a su trouver de l'ordre caché sous le désordre apparent. Mais ce nouvel ordre est très différent de l'ordre ancien^{[réf. nécessaire]} : au déterminisme implacable d'une dynamique intégrable quasi-périodique^{[réf. nécessaire]} a succédé une description de nature fondamentalement probabiliste^{[réf. nécessaire]}, caractérisée par l'existence d'invariants prenant la forme de mesures de probabilités, d'attracteurs, de dimensions fractales… Toutes les sciences, y compris sociales, sont concernées^{[réf. nécessaire]} par ce changement de paradigme.

Le déterminisme, de Laplace à Poincaré

Article détaillé : Déterminisme.

La stabilité du système solaire

Article détaillé : Problème à N corps.

Le point de départ de la théorie du chaos est le problème à « 3 corps » qui consiste à étudier le mouvement de trois corps en interaction gravitationnelle, comme par exemple le système : { Soleil - Terre - Lune}, supposé isolé du reste de l'univers. Le but de cette recherche est de déterminer si le système solaire est « stable » sur le long terme, ou bien si l'un des corps risque un jour de percuter un autre corps, ou encore être éjecté du système solaire vers l'infini.

Le problème à 3 corps est aussi vieux que la mécanique newtonienne ; en effet, dès la naissance de cette théorie, son fondateur s'est intéressé au problème à trois corps dans le but de prédire le mouvement de la Lune. Tous les astronomes à sa suite ont abordé ce problème, dont Laplace, qui crut avoir prouvé la stabilité du système solaire en utilisant la théorie des perturbations au premier ordre. Malheureusement, le développement perturbatif au premier ordre est insuffisant pour conclure définitivement. Un siècle après Laplace, Henri Poincaré s'est donc emparé du problème. On examine ci-dessous l'évolution des idées qui distingue la pensée de Laplace de celle de Poincaré.

Notion de système dynamique différentiel conservatif

Article détaillé : Système dynamique.

Pour un système possédant n degrés de libertés, l'espace des phases Γ du système possède 2n dimensions, de telle sorte que l'état complet 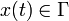$x(t) \in \Gamma$ du système à l'instant t est en général un vecteur à 2n composantes. On considère alors typiquement un système différentiel du premier ordre du type^[4] :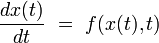

$\frac{dx(t)}{dt} \ = \ f(x(t),t)$

où la fonction f définit le système dynamique étudié (c'est en général également un vecteur à n dimensions, c’est-à-dire un ensemble de n fonctions scalaires). Ce système physique, supposé conservatif, est déterministe si et seulement si la dynamique du système associe à chaque condition initiale x₀ un et un seul état final x(t). Il faut pour cela qu'il existe une application bijective 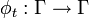$\phi_t : \Gamma \to \Gamma$ de l'espace des phases sur lui-même telle que :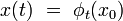

$x(t) \ = \ \phi_t(x_0)$

Lorsque le temps t varie, cette bijection engendre un flot sur Γ, c’est-à-dire un groupe continu à un paramètre φ_t. Cette modélisation mathématique correspond par exemple au flot hamiltonien de la mécanique classique, ainsi qu'au flot géodésique.

Laplace, ou le déterminisme triomphant

Fort des succès obtenus en mécanique céleste, Laplace écrit en 1814 dans l'introduction de son Essai philosophique sur les probabilités^[5] :

« Nous devons donc envisager l'état présent de l'univers comme l'effet de son état antérieur, et comme la cause de celui qui va suivre. Une intelligence qui pour un instant donné connaîtrait toutes les forces dont la nature est animée et la situation respective des êtres qui la composent, si d'ailleurs elle était assez vaste pour soumettre ses données à l'analyse, embrasserait dans la même formule les mouvements des plus grands corps de l'univers et ceux du plus léger atome : rien ne serait incertain pour elle, et l'avenir comme le passé serait présent à ses yeux.

L'esprit humain offre, dans la perfection qu'il a su donner à l'Astronomie, une faible esquisse de cette intelligence. Ses découvertes en Mécanique et en Géométrie, jointes à celle de la pesanteur universelle, l'ont mis à portée de comprendre dans les mêmes expressions analytiques les états passés et futurs du système du monde. En appliquant la même méthode à quelques autres objets de ses connaissances, il est parvenu à ramener à des lois générales les phénomènes observés, et à prévoir ceux que des circonstances données doivent faire éclore. Tous ces efforts dans la recherche de la vérité tendent à le rapprocher sans cesse de l'intelligence que nous venons de concevoir, mais dont il restera toujours infiniment éloigné. Cette tendance propre à l'espèce humaine est ce qui la rend supérieure aux animaux, et ses progrès en ce genre distinguent les nations et les siècles et font leur véritable gloire. »

Ce texte aujourd'hui célèbre est en réalité largement prophétique, au sens où Laplace ne possède pas le théorème général d'existence et d'unicité de la solution d'une équation différentielle, qui sera démontré ultérieurement, et fait l'objet du paragraphe suivant.

Le théorème de Cauchy-Lipschitz

Article détaillé : Théorème de Cauchy-Lipschitz.

C'est le mathématicien Cauchy qui énonce en 1820 le théorème général d'existence et d'unicité de la solution d'une équation différentielle. Lipschitz lui donnera sa forme définitive en 1868.

Poincaré et imprédictibilité

Environ un siècle après Laplace, Poincaré écrit dans l'introduction de son Calcul des Probabilités ^[6] un texte dont la tonalité est fort différente de celui de son illustre prédécesseur. C'est entre 1880 et 1910, que Poincaré, qui cherche à prouver la stabilité du système solaire, découvre un nouveau continent issu des équations de Newton et jusqu'alors inexploré.

« Comment oser parler des lois du hasard ? Le hasard n'est-il pas l'antithèse de toute loi ? Ainsi s'exprime Rerirand, au début de son Calcul des probabilités. La probabilité est opposée à la certitude ; c'est donc ce qu'on ignore et, par conséquent semble-t-il, ce qu'on ne saurait calculer. Il y a là une contradiction au moins apparente et sur laquelle on a déjà beaucoup écrit.

Et d'abord qu'est-ce que le hasard ? Les anciens distinguaient les phénomènes qui semblaient obéir à des lois harmonieuses, établies une fois pour toutes, et ceux qu'ils attribuaient au hasard ; c'étaient ceux qu'on ne pouvait prévoir parce qu'ils étaient rebelles à toute loi. Dans chaque domaine, les lois précises ne décidaient pas de tout, elles traçaient seulement les limites entre lesquelles il était permis au hasard de se mouvoir. […]

Pour trouver une meilleure définition du hasard, il nous faut examiner quelques-uns des faits qu'on s'accorde à regarder comme fortuits, et auxquels le calcul des probabilités paraît s'appliquer ; nous rechercherons ensuite quels sont leurs caractères communs. Le premier exemple que nous allons choisir est celui de l'équilibre instable ; si un cône repose sur sa pointe, nous savons bien qu'il va tomber, mais nous ne savons pas de quel côté ; il nous semble que le hasard seul va en décider. Si le cône était parfaitement symétrique, si son axe était parfaitement vertical, s'il n'était soumis à aucune autre force que la pesanteur, il ne tomberait pas du tout. Mais le moindre défaut de symétrie va le faire pencher légèrement d'un côté ou de l'autre, et dès qu'il penchera, si peu que ce soit, il tombera tout à fait de ce côté. Si même la symétrie est parfaite, une trépidation très légère, un souffle d'air pourra le faire incliner de quelques secondes d'arc ; ce sera assez pour déterminer sa chute et même le sens de sa chute qui sera celui de l'inclinaison initiale. »

« Une cause très petite, qui nous échappe, détermine un effet considérable que nous ne pouvons pas ne pas voir, et alors nous disons que cet effet est dû au hasard. Si nous connaissions exactement les lois de la nature et la situation de l'univers à l'instant initial, nous pourrions prédire exactement la situation de ce même univers à un instant ultérieur. Mais, lors même que les lois naturelles n'auraient plus de secret pour nous, nous ne pourrions connaître la situation qu'approximativement. Si cela nous permet de prévoir la situation ultérieure avec la même approximation, c'est tout ce qu'il nous faut, nous disons que le phénomène a été prévu, qu'il est régi par des lois ; mais il n'en est pas toujours ainsi, il peut arriver que de petites différences dans les conditions initiales en engendrent de très grandes dans les phénomènes finaux ; une petite erreur sur les premières produirait une erreur énorme sur les derniers. La prédiction devient impossible et nous avons le phénomène fortuit. »

Sensibilité aux conditions initiales

Dans le paragraphe précédent, Poincaré met en exergue le phénomène connu aujourd'hui sous la dénomination de sensibilité aux conditions initiales : pour un système chaotique, une très petite erreur sur la connaissance de l'état initial x₀ dans l'espace des phases va se trouver (presque toujours) rapidement amplifiée.

Quantitativement, la croissance de l'erreur est localement exponentielle pour les systèmes fortement chaotiques, baptisés selon la théorie ergodique K-systèmes (le K est pour Kolmogorov), ainsi que pour les systèmes très fortement chaotiques, dits B-systèmes (le B est pour Bernoulli) ^[7]. Cette amplification des erreurs rend rapidement totalement inopérant le pouvoir prédictif qui découle de l'unicité de la solution, assurée par Cauchy-Lipschitz.

Typiquement, pour un système chaotique, les erreurs croissent localement selon une loi du type :

$\displaystyle{e^\frac{t}{\tau}}$

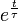
où τ est un temps caractéristique du système chaotique, appelé parfois « horizon de Lyapounov » ^[8]. Le caractère prédictible de l'évolution du système ne subsiste que pour les instants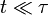 $t \ll \tau$, pour lesquels l'exponentielle vaut approximativement 1, et donc tels que l'erreur garde sa taille initiale. En revanche, pour 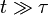$t \gg \tau$, toute prédiction devient pratiquement impossible, bien que le théorème de Cauchy-Lipschitz reste vrai.

Poincaré et après

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Poincaré & la stabilité du système solaire

Article détaillé : Problème à N corps.

Un siècle après Laplace, Henri Poincaré s'est attelé au problème de la stabilité du système solaire. Entre 1880 et 1886, il commence par publier une série de mémoires intitulés : «Sur les courbes définies par une équation différentielle» qui donne naissance à l'analyse qualitative des équations différentielles. Poincaré y introduit notamment la notion capitale de portrait de phase, qui résume géométriquement l'aspect des solutions dans l'espace des phases du système. Puis, en 1890, il publie le fameux mémoire intitulé : «Sur le problème des trois corps et les équations de la dynamique», qui lui vaudra le prix du roi Oscar, roi de Norvège et de Suède et passionné de mathématiques^[9]. L'histoire est célèbre^[10] : le mémoire lauréat comportait une erreur détectée par le jeune mathématicien Phrägmen alors qu'il prépare le manuscrit pour l'imprimeur. Cette erreur obligera Poincaré à procéder à de profonds remaniements dans son mémoire, et aussi à rembourser les frais d'impression du premier mémoire, une somme supérieure de quelque mille couronnes au prix qu'il avait reçu. Mais cette erreur fut féconde, car en lieu et place de la stabilité du système solaire, Poincaré découvrit le chaos potentiel caché dans les équations de la dynamique.

Plus récemment, des calculs numériques effectués par l'astronome Jacques Laskar en 1989-1990^[11], puis confirmés par Sussman & Wisdom en 1992^[12], ont montré que le système solaire est chaotique, avec un horizon de Lyapounov de l'ordre de 200 millions d'années.

L'école russe des années 1890-1950

Lyapounov & la stabilité du mouvement

Le 12 octobre 1892, Lyapounov soutient à l'Université de Moscou une thèse de doctorat intitulée : Le problème général de la stabilité du mouvement. Il y introduit l'idée de mesurer la divergence possible entre deux orbites issues de conditions initiales voisines. Lorsque cette divergence croit exponentiellement avec le temps pour presque toutes les conditions initiales voisines d'un point donné, on a le phénomène de sensibilité aux conditions initiales, idée à laquelle sont attachés les exposants de Lyapounov, qui donnent une mesure quantitative de cette divergence exponentielle locale^[13].

L'école de Gorki : 1930-1940

• Andronov
• Pontryagin
• Lefschetz

L'oscillateur de Van der Pol

Article détaillé : Oscillateur de Van der Pol.

Émergence & développement de la théorie ergodique

Article détaillé : Théorie ergodique.

• Émergence
• Birkhoff
• Von Neumann
• Koopman
• Hopf
• Hedlung

Prédictibilité & calculabilité

Norbert Wiener et John von Neumann se sont préoccupés pourtant de la possibilité de prédire par le calcul une situation future à partir d'un état présent. Si Wiener jugeait la tâche ardue, voire impossible puisque de « petites causes » qu'on omettrait nécessairement d'inclure dans le modèle peuvent produire de « grands effets » (il donna l'image du « flocon de neige déclenchant une avalanche »), Von Neumann y voyait une occasion exceptionnelle pour les nouveaux appareils que l'on n'avait pas encore baptisés ordinateurs : « Si un flocon de neige peut déclencher une avalanche », répondait-il à Wiener, « alors la prédiction par le calcul nous dira très exactement quel flocon de neige précis intercepter pour que l'avalanche ne se produise pas ! » Wiener se montra sceptique : un état hypercritique restait un état hypercritique, et supprimer ce flocon particulier ne ferait à son avis que « permettre à un autre de le remplacer dans cette fonction ». Selon lui, rien ne serait donc résolu (point de vue admis aujourd'hui). Les deux hommes ne poussèrent pas plus avant ce différend.

Lorenz & la météorologie

Article détaillé : Système dynamique de Lorenz.

Présentation

En 1963, le météorologue Lorenz mit en évidence le caractère vraisemblablement chaotique de la météorologie^[14].

Mathématiquement, le couplage de l'atmosphère avec l'océan est décrit par le système d'équations aux dérivées partielles couplées de Navier-Stokes de la mécanique des fluides. Ce système d'équations était beaucoup trop compliqué à résoudre numériquement pour les premiers ordinateurs existant au temps de Lorenz. Celui-ci eut donc l'idée de chercher un modèle très simplifié de ces équations pour étudier une situation physique particulière : le phénomène de convection de Rayleigh-Bénard. Il aboutit alors à un système dynamique différentiel possédant seulement trois degrés de liberté, beaucoup plus simple à intégrer numériquement que les équations de départ. Il observa alors, par pur hasard, qu'une modification minime des données initiales (de l'ordre de un pour mille) entraînait des résultats très différents. Lorenz venait de mettre en exergue la sensibilité aux conditions initiales (déjà observée en analyse numérique dans des résolutions d'équations différentielles sur ordinateur, entre autres par Marion Créhange à l'Université de Nancy).

La métaphore du papillon

En 1972, Lorenz fait une conférence à l'American Association for the Advancement of Science intitulée^[15]: « Predictability: Does the Flap of a Butterfly's Wings in Brazil Set off a Tornado in Texas? », qui se traduit en français par :

« Prédictibilité : le battement d'ailes d'un papillon au Brésil provoque-t-il une tornade au Texas ? ».

Cette métaphore, devenue emblématique du phénomène de sensibilité aux conditions initiales, est souvent interprétée à tort de façon causale : ce serait le battement d'aile du papillon qui déclencherait la tempête. Il n'en est rien ; Lorenz écrit en effet^[16]:

« De crainte que le seul fait de demander, suivant le titre de cet article, "un battement d'aile de papillon au Brésil peut-il déclencher une tornade au Texas ?", fasse douter de mon sérieux, sans même parler d'une réponse affirmative, je mettrai cette question en perspective en avançant les deux propositions suivantes :

• Si un seul battement d'ailes d'un papillon peut avoir pour effet le déclenchement d'une tornade, alors, il en va ainsi également de tous les battements précédents et subséquents de ses ailes, comme de ceux de millions d'autres papillons, pour ne pas mentionner les activités d'innombrables créatures plus puissantes, en particulier de notre propre espèce.

• Si le battement d'ailes d'un papillon peut déclencher une tornade, il peut aussi l'empêcher. ».

Il serait plus juste de dire que le battement d'ailes du papillon "induit" la tornade, il ne la provoque pas directement ! Elle est provoquée par des conditions locales, qui sont elles-mêmes "liées" à d'autres, etc . . .
C'est là que les conditions d'apparition de la tornade sont indirectement liées au battement d'ailes du papillon (ainsi qu'à une multitude d'autres effets), et que cette sensibilité aux conditions initiales est justifiée.

Stephen Smale : topologie & stabilité structurelle

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

L'école russe des années 1950-1980

Article détaillé : Système d'Anosov.

• Anososv

Article détaillé : Théorème KAM.

• Sinaï
• Arnold

Transition d'une dynamique régulière vers le chaos

Soit un système dynamique dépendant d'un paramètre μ :

$\frac{dx(t)}{dt} \ = \ f_{\mu}(x(t),t)$

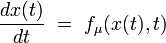
Il arrive que la dynamique change de comportement lorsque le paramètre μ varie. On a pu mettre en évidence trois grands scénarios de passage d'une dynamique régulière à une dynamique chaotique lors de la variation d'un paramètre.

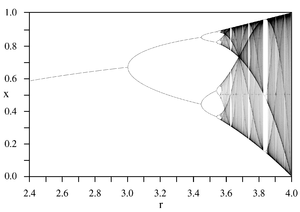
Scénario de Feigenbaum

Feigenbaum a proposé un scénario dit : « par doublement de période » pour décrire la transition d'une dynamique régulière vers le chaos. Ce scénario trouve son origine dans le comportement de la suite logistique, qui est définie par récurrence par une application du segment [0, 1] dans lui-même :

$x_{n+1} \ = \ \mu \, x_n \ (1 - x_n)$

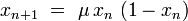
où n = 0, 1, … dénote le temps discret, x l'unique variable dynamique, et 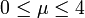$0 \le \mu \le 4$ un paramètre^[17]. La dynamique de cette application présente un comportement très différent selon la valeur du paramètre μ :

• Pour 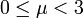$0 \le \mu < 3$, le système possède un point fixe attractif, qui devient instable lorsque μ = 3.

• Pour 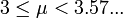$3 \le \mu < 3.57...$, l'application possède un attracteur qui est une orbite périodique, de période 2ⁿ où n est un entier qui tend vers l'infini lorsque μ tend vers 3.57…

• Lorsque μ = 3.57..., l'application possède un attracteur de Feigenbaum fractal (mais non étrange) découvert par le biologiste May (1976)^[18].

• Le cas μ = 4 avait été étudié dès 1947 par Ulam et von Neumann^[19]. À noter qu'on peut dans ce cas précis établir l'expression exacte de la mesure invariante ergodique ^[20].

Bifurcation vers le chaos par doublement de période

Lorsque le paramètre μ augmente, on obtient donc une succession de bifurcations de la régularité vers le chaos, résumée sur la figure ci-contre.

Scénario de Ruelle-Takens

Par quasi-périodicité…

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Scénario de Pomeau-Manneville

Par intermittence…

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Quelques exemples

• Transformation du boulanger. La transformation du boulanger a de nombreuses variantes, qui toutes ont pour point commun de « faire remonter » très vite au niveau macroscopique d'infimes différences microscopiques, plus faible que la résolution de l'instrument utilisé.
• Transformation du photomaton.

Bibliographie

Bibliothèque virtuelle

• David Ruelle ; Chaos, imprédictibilité et hasard, conférence de vulgarisation donnée en 2000 par l'auteur à l'Université de tous les savoirs, puis publiée dans : Qu'est-ce que l'Univers ? (éd. Y. Michaud), Odile Jacob (2000), 647-656. Texte complet disponible au format pdf.

• Académie des sciences morales et politiques ; Le chaos, dans : Implications philosophiques de la science contemporaine (2001), groupe de travail présidé par Bernard d'Espagnat :
  • François Lurcat ; Le chaos & l'occident, format pdf.
  • Éric Bois ; De quelques enjeux philosophiques du phénomène du chaos, format pdf.
  • Débat, format pdf.

• Predrag Cvitanovic´, Roberto Artuso, Ronnie Mainieri & Gábor Vattay ; The Chaos Webbook, (Version 11 - Décembre 2004). Ouvrage de référence en ligne écrit par Predrag Cvitanovic´ (Niels Bohr Institute, Copenhague) et ses collaborateurs.

Ouvrages de vulgarisation

• Amy Dahan Dalmedico, Jean-Luc Chabert & Karine Chemla (sous la direction de) ; Chaos & déterminisme, Points Sciences, Le Seuil (1992), ISBN 2-02-015182-0. Un ouvrage collectif au format poche, divisé en trois parties : Approches mathématiques, Physique & Calcul, et Quelques retours sur l'histoire et la philosophie, écrits par quelques-uns des meilleurs spécialistes actuels du domaine.

• David Ruelle ; Hasard & Chaos, Collection Opus 89, Editions Odile Jacob (1991), ISBN 2-7381-0665-X. Ouvrage d'introduction au chaos au format poche par un expert, professeur de physique théorique à l'Institut de hautes études scientifiques de Bures-sur-Yvette, et auteur de nombreuses contributions au domaine.

• Pierre Bergé, Yves Pomeau & Monique Dubois-Gance ; Des rythmes au chaos, Collection Opus 64, Editions Odile Jacob (1997), ISBN 2-7381-0524-6. Un autre ouvrage d'introduction au format poche, par des spécialistes français.

• Florin Diacu & Philip Holmes ; Celestial Encounters - The Origin of Chaos, Princeton University Press (1996), ISBN 0-691-00545-1. L'origine du "chaos" moderne se trouve dans les travaux pionniers d'Henri Poincaré réalisés à la fin du XIX^e siècle à propos d'un vieux problème de mécanique newtonienne : le problème à N corps. Les auteurs , mathématiciens spécialistes du domaine, retracent l'histoire de ce problème et de ses développements de Poincaré à nos jours. Vulgarisation accessible à partir du premier cycle universitaire.

• Ivar Ekeland, Le chaos, Dominos, Flammarion (1995), ISBN 2-08-035172-9. Un ouvrage vulgarisant les notions de la théorie du chaos.

• James Gleick, La Théorie du chaos, Albin Michel (1989), ISBN 2-226-03635-0. Réédité par Flammarion (1991), ISBN . Ouvrage écrit par un journaliste.

• John Briggs & David Peat, Un miroir turbulent, Dunod (1997), ISBN 2-7296-0348-4. Un ouvrage de vulgarisation de la théorie du chaos.

Textes techniques

• Pierre Bergé, Yves Pomeau & Christian Vidal ; L'ordre dans le chaos - Vers une approche déterministe de la turbulence, Hermann (1988), ISBN 2-7056-5980-3. Un ouvrage d'introduction au chaos par des experts français, accessible dès le premier cycle universitaire. Prix Henri Poincaré 1990 de l'Académie des Sciences.

• Christophe Letellier ; Le Chaos dans la nature, Vuibert (2006), ISBN 2-7117-9140-8. Un ouvrage d'introduction tant aux aspects historiques qu'aux concepts techniques par un expert français.

• T. W. B. Kibble & F.H. Berkshire ; Classical Mechanics, Prentice Hall (4^e édition-1997), ISBN 0-582-25972-X. Un excellent cours d'introduction à la mécanique, des fondements newtoniens jusqu’aux formalismes plus avancés de Lagrange et de Hamilton. Kibble est professeur émérite de Physique Théorique de l'Imperial College de Londres. Pour cette 4^e édition (avec un co-auteur), deux chapitres d'introduction aux idées de la théorie du chaos ont été inclus. Niveau : à partir du premier cycle universitaire. (N.B. : Il a existé une traduction française de l'édition précédente, publiée en son temps par Dunod.)

• K. Alligood, T. Sauer & J. A. Yorke ; Chaos: An Introduction to Dynamical Systems, Springer-Verlag (1997), ISBN 0-387-94677-2.

• David Ruelle ; Deterministic chaos: the science and the fiction, Proceedings of the Royal Society London A 427 (1990), 241-248.

• Henri Poincaré ; Les méthodes nouvelles de la mécanique céleste, 3 volumes, Éditions Gauthiers-Villars (1892).

• Jacques Hadamard ; Les surfaces à courbures opposées et leurs lignes géodésiques, Journal de Mathématiques Pures & Appliquées 4 (1898) 27. Pour une revue plus récente, voir e.g. la référence suivante : Pierre Pansu ; Le flot géodésique des variétés Riemanniennes à courbure négative, Séminaire Bourbaki 738 (1991) publié dans : Astérisque 201-203 (1991) 269-298.

• Vladimir I. Arnold ; Mathematical Methods of Classical Mechanics, Springer-Verlag (2^e édition-1989), ISBN 0-387-96890-3. Une synthèse de l'état de l'art en mécanique analytique (formalismes lagrangien & hamiltonien) avec l'accent mis sur l'interprétation géométrique de ces formalismes, par l'un des plus brillants mathématiciens du domaine. À partir du second cycle universitaire.

• Vladimir I. Arnold, V.V. Kozlov & A.I. Neishtadt ; Mathematical Aspects of Classical and Celestial Mechanics, Encyclopaedia of Mathematical Sciences, Springer-Verlag (2^e édition-1993). Une synthèse de l'état de l'art en mécanique céleste, par l'un des plus brillants mathématiciens du domaine (Arnold) et ses collaborateurs. À partir du second cycle universitaire.

• Vladimir Arnold & André Avez ; Ergodic problems of classical mechanics, Advanced Book Classics, Addison-Wesley (1988), ISBN . Réédition d'un ouvrage classique écrit en 1968.

• David Ruelle & Jean-Pierre Eckmann ; Ergodic theory of chaos and strange attractors, Review of Modern Physisc 57 (1985), 617-656.

• Vladimir Damgov, Nonlinear and parametric phenomena - Applications in radiophysical and mechanical systems, World Scientific, Series on Nonlinear Sciences, 2004.

Aspects historiques

• Amy Dahan & David Aubin ; Writing the History of Dynamical Systems and Chaos : Longue Durée and Revolution, Disciplines and Culture, Historia Mathematica 29 (2002), 273-339. Texte complet disponible au format pdf.

• Amy Dahan ; Le chaos a-t-il engendré une révolution scientifique ?, La Recherche (janvier 2000).

• Amy Dahan ; Le difficile héritage de Henri Poincaré en systèmes dynamiques, in Greffe, J., Heinzmann, G., & Lorenz, K., (eds.) ; Henri Poincaré, science et philosophie, Berlin, Akademie Verlag & Paris, Blanchard (1997), 13-33.

• David Aubin ; A Cultural History of Catastrophes and Chaos: Around the Institut des Hautes Études Scientifiques, France 1958-1980, Thèse de doctorat (Ph. D.), Princeton University (1998), UMI #9817022. Texte complet disponible au format pdf.

Notes et références

1. ↑ Pour un système dynamique différentiable décrit par une équation différentielle, deux degrés de liberté suffisent. Pour un système dynamique non différentiable décrit par une application discrète, un seul degré de liberté est suffisant.
2. ↑ Bien sûr, un système complexe peut aussi posséder une dynamique d'une grande complexité : mentionnons par exemple les phénomènes météorologiques ou l'économie.
3. ↑ Tien-Yien Li & James A. Yorke ; Period three implies chaos, American Mathematical Monthly 82 (1975), 985-992.
4. ↑ Rappelons qu'une équation différentielle d'ordre n peut toujours se ramener à un système de n équations différentielles couplées d'ordre un.
5. ↑ Pierre-Simon Laplace ; Essai philosophique sur les probabilités, (Paris, 1814) ; Edition des « Maîtres de la pensée scientifique », Gauthier-Villars (Paris, 1921) pp. 3-4.
6. ↑ Henri Poincaré ; Calcul des probabilités, Gauthier-Villars (Paris - 2^e édition, 1912). Réimpression : Éditions Jacques Gabay (Paris-1987).
7. ↑ On a l'implication : 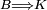$\scriptstyle{B \Longrightarrow K}$, la réciproque étant fausse en général. Les systèmes K et B possèdent une entropie de Kolmogorov-Sinaï positive.
8. ↑ L'inverse du temps $\scriptstyle{\tau}$ est appelé un exposant de Lyapounov.
9. ↑ Le jury est composé de Weierstrass, Mittag-Lefflet et Hermite.
10. ↑ June Barrow-Green ; Poincaré & the three-body problem, History of Mathematics (Vol. 11), American Mathematical Society & London Mathematical Society (1997).
11. ↑ Lire e.g. : Jacques Laskar ; La stabilité du système solaire, dans : Amy Dahan Dalmedico, Jean-Luc Chabert & Karine Chemla (sous la direction de) ; Chaos & déterminisme, Points Sciences, Le Seuil (1992), ISBN 2-02-015182-0 ; et : Jacques Laskar ; Chaos in the Solar System, conférence pleinière donnée à TH2002 (Paris-Juillet 2002). Format pdf.
12. ↑ G.J. Sussman & J. Wisdom ; Chaotic evolution of the solar system, Science 257 (1992), 56-62.
13. ↑ La divergence n'est en général exponentielle que localement. Rappelons en effet qu'un système chaotique possède le plus souvent un espace des phases compact, propriété qui permet l'existence d'un phénomène de récurrence.
14. ↑ Edward N. Lorenz, Deterministic non-periodic flow, Journal of the Atmospheric Sciences 20(2) (1963), 130–141. Format pdf.
15. ↑ Le titre n'est en fait pas de Lorenz, mais d'un autre météorologue, Philip Merilees, organisateur de la conférence ; Lorenz l'a découvert trop tard pour pouvoir en changer. Cf. Nicolas Witkowski : La chasse à l'effet papillon, Alliage 22 (1995), 46-53.
16. ↑ Edward N. Lorenz ; Un battement d'aile de papillon au Brésil peut-il déclencher une tornade au Texas ?, Alliage 22 (1993), 42-45. Traduction française du texte de la conférence de 1972, publié (en anglais) dans : The essence of chaos, The Jessie and John Danz Lecture Series, University of Washington Press (1993). Ce livre contient une série de conférences de vulgarisation données à l'université de Washington (Seattle) en 1990.
17. ↑ Lorsque le paramètre $\scriptstyle{\mu}$ devient supérieur à quatre, l'application sort de l'intervalle [0, 1].
18. ↑ R.M. May ; Nature 261 (1976), 459.
19. ↑ Stanislas Ulam & John Von Neumann ; Bulletin of the American Mathematical Society 53 (1947), 1120.
20. ↑ Pierre Collet & Jean-Pierre Eckmann ; Iterated Maps on the Interval as Dynamical Systems, Birkhaüser (1980).

Articles connexes

• Déterminisme
• Mécanique hamiltonienne
• Système intégrable
• Théorème KAM
• Problème à N corps
• Théorie ergodique
• Système dynamique
• Chaos quantique

Liens externes

• Découverte de la théorie du chaos de A à Z
• Contrôle de systèmes chaotiques

Ce document provient de « Th%C3%A9orie du chaos ».