- Theoreme de projection sur un convexe ferme
-
Théorème de projection sur un convexe fermé
En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance qui généralise la projection orthogonale sur un espace vectoriel. Il remplace avantageusement le théorème de Hahn-Banach dans le cas de l'espace de Hilbert. Il est en effet plus simple à démontrer et plus puissant dans ses conséquences. En revanche il est moins général car il impose l'utilisation d'une norme issue d'un produit scalaire.
Il possède de nombreuses applications, en analyse fonctionnelle, en algèbre linéaire, en théorie des jeux, pour la modélisation mathématiques des sciences économiques ou encore pour la programmation linéaire.
Sommaire
Énoncé du théorème
Dans cet article E désigne un espace vectoriel muni d'un produit scalaire, x désigne un vecteur et C un ensemble convexe complet de E. La distance entre x et C désigne la borne inférieure des distances entre x et un point de C.
La version la plus générale du théorème est la suivante :
Théorème de la projection sur un convexe fermé — Il existe une unique application t de E dans C, dite projection sur le convexe, qui à x associe le point t(x) de C, tel que la distance de x à C soit égale à celle de x à t(x). Le vecteur t(x) est l'unique point de C vérifiant les deux propositions suivantes, qui sont équivalentes :
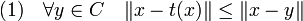
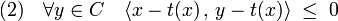
Dans le cas d'un Hilbert, c'est à dire d'un espace complet, il suffit que C soit fermé. L'application t est parfois dénommée projecteur de meilleure approximation[1]. Elle possède de plus les propriétés suivantes :
Propriétés de la projection — La projection t est idempotente, c'est-à-dire que la composée de t avec lui-même est égale à t ; elle est contractante, c'est-à-dire que les images de deux points sont à une distance moindre que leurs antécédents ; enfin elle est monotone au sens suivant :
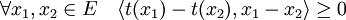
Corollaires
Article détaillé : Séparation des convexes.Le théorème de projection a pour corollaire important le théorème de Hahn-Banach dans le cas d'un espace de Hilbert. Dans ce paragraphe E désigne un Hilbert :
Théorème de Hahn-Banach dans un Hilbert — Soit F un sous-espace vectoriel fermé de E et f une forme linéaire continue de F, alors il existe une forme linéaire continue f' prolongeant f et ayant la même norme au sens des opérateurs.
Si, sous cette forme, le résultat ne présente guère d'intérêt car il est valable dans un contexte plus général, il possède néanmoins des extensions spécifiques aux Hilbert :
Généralisation — Soit G un espace de Hilbert et, avec les notations du théorème précédent a un opérateur continue de F dans G. Il existe un opérateur a' prolongeant a sur E et de même norme.
Ce résultat n'est plus vrai dans le cadre général d'un espace de Banach.
Il existe une autre forme du théorème de Hahn-Banach :
Premier théorème de séparation — Soit A et B deux sous-ensembles non vides et disjoints de E tel A-B est un convexe fermé. Il existe alors une forme linéaire continue f tel que :
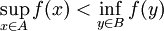
Ce résultat s'exprime encore sous la forme suivante :
Deuxième théorème de séparation — Soit A un convexe fermé et B un convexe compact tel que ni A ni B ne soit vide et que l'intersection de A et B soit vide. Alors il existe une forme linéaire continue tel que :
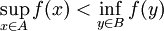
Dans le cas de la dimension finie, une forme du théorème de la séparation ne nécessite plus le caractère fermé du convexe :
Séparation en dimension finie — Si E est de dimension finie, soit x un élément de E et C un convexe ne contenant pas x, alors il existe une forme linéaire tel que :
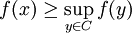
Applications
Ce théorème possède de multiples applications.
En algèbre linéaire, il permet par exemple d'établir les propriétés d'une projection orthogonale, cette approche est choisie dans l'article Espace euclidien. Il permet aussi de démontrer l'existence d'une base hilbertienne.
Il est utilisé en analyse fonctionnelle. Il offre un équivalent au théorème de Hahn-Banach disposant d'une démonstration plus simple et qui ne fait pas appel au lemme de Zorn, elle peut donner lieu à des algorithmes programmable en dimension finie. Un exemple est donné par le théorème de Stampacchia. Il permet aussi d'aider à la résolution d'équation aux dérivées partielles comme par exemple pour le théorème de Lax-Milgram qui utilise le cas particulier de convexe, un sous-espace vectoriel fermé.
En théorie des jeux, John von Neumann établit un théorème fondamental montrant l'existence de stratégies optimales pour les différents joueurs dans un contexte très général[2]. Ce résultat est une conséquence du théorème de projection dans le cadre d'un Hilbert. Il possède de nombreuses conséquences, dont l'une célèbre est l'existence d'un Optimum de Pareto sous des hypothèses pas trop contraignantes en sciences économiques[3].
En programmation linéaire, ce théorème est utilisé pour, par exemple dans le cas des théorèmes de l'alternative trouver des solutions à des systèmes d'inéquations linéaires[4].
Démonstrations
Théorème
-
- Montrons l'existence de t(x) :
Soit δ la distance entre x et C, (yn) une suite de C tel que le carré de la distance entre x et yn soit inférieur ou égal à δ2 - 1/n. Soit n et m deux entiers, alors les deux égalités suivantes sont vérifiées :
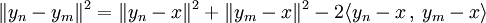
et
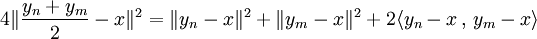
Elles démontrent l'égalité suivante :
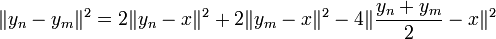
En majorant les deux premiers termes du second membre de l'égalité et en remarquant que le milieu de yn et ym est un point de C donc à une distance supérieure ou égal à δ de x, on obtient :
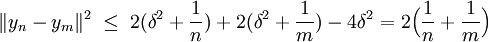
La dernière majoration établit le fait que la suite (yn) est de Cauchy donc convergente dans C qui est complet. La limite est un point de C, dont la distance à x est minimale.
-
- Montrons l'unicité de t(x) :
L'unicité du point atteignant le minimum se démontre à l'aide d'une remarque géométrique. Soient y1 et y2 deux points du convexe C à égale distance de x, le milieu des deux points est élément du convexe et est à une distance strictement plus petite que celle entre y1 et x. En conséquence deux points distincts de C à égale distance de x ne peuvent être des points à distance minimum.
Rappelons les deux majorations du théorème.
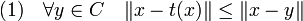
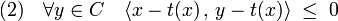
-
- Montrons que la propriété (1) implique (2) :
Soit y un élément de C, alors le barycentre θt(x) + (1 - θ)y, élément de C est plus éloigné de x que t(x), d'après la proposition (1), donc :
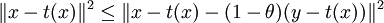
On en déduit la majoration :
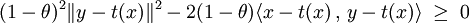
Cette égalité est vraie pour toute valeur de θ comprise entre zéro et 1. Il suffit alors de dériver cette fonction en θ au point un pour obtenir le résultat.
-
- Montrons que la propriété (2) implique (1) :
Un développement de la majoration (2) donne :
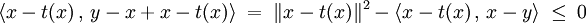
L'application de l'inégalité de Cauchy-Schwarz montre que :
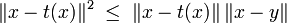
et permet de conclure.
Propriétés de la projection
-
- L'application t est idempotente :
En effet, si x est un élément de E, t(x) est élément de convexe, son image est donc lui-même.
-
- L'application t est contractante :
C'est une conséquence directe des deux majorations stipulant que : <t(x1) - x1 , t(x1) - t(x2> et <t(x2) - x2 , t(x2) - t(x1> sont tous deux inférieurs ou égaux à zéro. Il suffit de sommer ces deux inégalités et d'appliquer Cauchy-Schwarz.
-
- L'application t est monotone :
La somme des deux majorations de la démonstration précédente montre que le carré de la norme de t(x1) - t(x2) est toujours positif et inférieur ou égal à <t(x1) - t(x2) , x1 - x2 >.
Corollaires
-
- Il existe une forme linéaire continue f' prolongeant f et ayant la même norme au sens des opérateurs.
Il suffit de considérer le projecteur t sur F, il est linéaire (une démonstration ne faisant pas appel au caractère fini de la dimension est donnée dans l'article espace euclidien). L'application fot est une forme linéaire continue prolongeant f et ayant la même norme, en effet t est un projecteur orthogonal, donc de norme égale à un et :
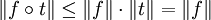
L'égalité des normes est obtenue car le prolongement est égal à f sur F.
-
- Il existe un opérateur a' prolongeant a sur E et de même norme.
Il suffit une fois encore de composer a par t le projecteur sur F.
Pour montrer les corollaires suivants, montrons tout d'abord un résultat intermédiaire :
-
- Soit C un convexe fermé non vide de E et x un élément de E hors de C. Alors il existe une forme linéaire continue f tel que l'image de x par f est strictement supérieure au sup de f sur C.
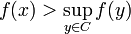
Soit t la projection sur C et f la forme linéaire définie par :
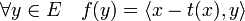
Les vecteurs x et t(x) ne sont pas confondus car x n'est pas élément de C, et donc si λ désigne la distance entre x et C :
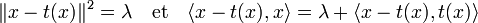
La deuxième caractérisation du projecteur montre que :

L'utilisation de la dernière majoration dans l'égalité précédente montre :
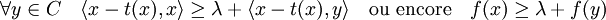
Ce qui démontre le résultat intermédiaire.
-
- Soit A et B deux sous-ensembles non vides et disjoints de E tel A - B est un convexe fermé. Il existe une forme linéaire continue f tel que :
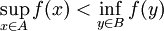
L'ensemble A - B est un convexe fermé ne contenant pas le vecteur nul. Le résultat précédent montre l'existence d'une forme f tel que :

Ce qui démontre la proposition.
-
- Le resultat précédent reste vrai si A est un convexe fermé et B un convexe compact.
Montrons que A - B est fermé. Soit c un élément de l'adhérence de l'ensemble, alors il existe deux suites (an) et (bn) l'une d'éléments de A et l'autre d'éléments de B tel que la différence converge vers c. Soit (bφ(n)) une suite extraite convergente, dont l'existence est garantie par le fait que B est compact. La différente des suites (aφ(n)) et (bφ(n)) est convergente vers c car extraite d'une suite convergente vers c. La convergence de la deuxième démontre alors celle de la première. Soit a (resp. b) la limite de (aφ(n)) (resp. (bφ(n))). Par passage à la limite, c apparaît comme la différence du point a élément de A car l'ensemble est fermé et b élément de B pour la même raison. Ceci démontre que A - B est fermé. Les hypothèses de la proposition précédente sont rassemblées car A - B est convexe, elles permettent de conclure.
-
- Si E est de dimension finie, soit x un élément de E et C un convexe ne contenant pas x, alors il existe une forme linéaire tel que :
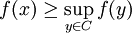
Soit Ty l'ensemble des formes linéaires f de la boule unité fermée dont l'image de x - y soit strictement positive. L'objectif est de montrer que l'intersection de tous les Ty, si y décrit C est non vide, en effet :
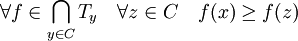
La propriété suivante permet de conclure :
Soit K un compact et (Fλ) une famille de fermés de K. Si l'intersection de tous les Fλ est vide, alors il existe une suite finie (λ1, ..., λn) tel que l'intersection des fermés indexés par (λ1, ..., λn) est aussi vide.
Cette propriété correspond au passage par le complémentaire de la définition d'un compact. La sphère unité des formes linéaires est compact car la dimension est finie. Les Ty sont fermés car image réciproque d'un fermé par une application continue. Il suffit donc de démontrer que toute intersection finie des Ty est non vide.
Soit (y1, ..., yn) une famille de points de C et K l'enveloppe convexe de cette famille. Elle forme un convexe fermé et ne contient pas x. Le troisième corollaire montre l'existence d'une forme linéaire f tel que :
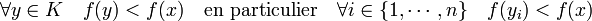
Ce qui termine la démonstration.
Notes et références
Notes
- ↑ J. P. Aubin Analyse fonctionnelle appliquée Puf 1987 p 28 (ISBN 02463822)
- ↑ John von Neumann Zur Theorie der Gesellschaftsspiele Mathematische Annalen Bd. 100. Berlin, Springer 1928 p 295 320
- ↑ Les textes sur ce sujet sont nombreux, on trouve par exemple :M. Voorneveld Pareto-Optimal Security Strategies as Minimax Strategies of a Standard Matrix Game Journal of Optimization Theory and Applications Hollande 2004 p 203-210
- ↑ G. Dantzig et M. Thapa Linear Programming 2: Theory and Extensions, Springer, 2003 (ISBN 978-0387986135)
Liens externes
- (fr) Projection dans un espace de Hilbert par les mathématiques.net
- (fr) Espaces de Hilbert un cours de Maîtrise d'analyse fonctionnelle par l'Université de Cergy 2006
Références
- J. P. Aubin Analyse fonctionnelle appliquée Puf 1987 (ISBN 02463822)
L'essentiel des démonstrations ainsi que des exemples proviennent de ce livre.- Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
Ce sujet est rapidement traité en page 79.Théorèmes de l'analyse fonctionnelleThéorème d'Ascoli • Théorème de Baire • Théorème de Banach-Alaoglu • Théorème de Banach-Mazur • Théorème de Banach-Schauder • Théorème de Banach-Steinhaus • Théorème du graphe fermé • Théorème de Hahn-Banach • Théorème de Lax-Milgram
- Portail des mathématiques
Catégories : Géométrie convexe | Algèbre bilinéaire | Théorème de mathématiques -
Wikimedia Foundation. 2010.
