Suite logistique

En mathématiques, une suite logistique est un exemple simple de suite dont la récurrence n'est pas linéaire. Souvent citée comme exemple de la complexité pouvant surgir de simple relation non linéaire, cette suite fut popularisée par le biologiste Robert May en 1976.

Sa relation de récurrence est

$x_{n+1} = \mu x_n(1 - x_n)~$

Elle conduit, suivant les valeurs de μ, à une suite convergente, une suite soumise à oscillations ou une suite chaotique.

Elle est la solution en temps discret du modèle de Verhulst. Le terme « logistique » provient de l'ouvrage de Pierre François Verhulst qui appelle courbe logistique la solution en temps continu de son modèle. Il écrit en 1845 dans son ouvrage consacré à ce phénomène : « Nous donnerons le terme de logistique à cette courbe ». L'auteur n'explique pas son choix mais « logistique » a même racine que logarithme et logistikos signifie « calcul » en grec^[1].

Comportement selon µ

Dans le modèle logistique, la variable notée ici x_n désigne l’effectif de la population d'une espèce. En faisant varier le paramètre µ, plusieurs comportements différents sont observés :

• Si 0≤µ≤1, l’espèce finira par mourir, quelle que soit la population de départ. Autrement dit, $\lim_{+\infty} x_n = 0$.
• Si 1≤µ≤2, la population finit par se stabiliser autour de la valeur $\frac {\mu-1}{\mu}$, quelle que soit la population initiale. Autrement dit $\lim_{+\infty} x_n = \frac {\mu-1}{\mu}$.
• Si 2≤µ≤3, elle finit également par se stabiliser autour de $\frac {\mu-1}{\mu}$ après avoir oscillé autour pendant quelque temps. La vitesse de convergence est linéaire, sauf pour µ=3 où elle est très lente.
• Si 3<µ≤1+√6 (environ 3,45), elle finit par osciller entre deux valeurs, dépendantes de µ, mais pas de la population initiale.
• Si 3,45<µ<3,54 (environ), elle finit par osciller entre quatre valeurs, là encore dépendantes de µ mais pas de la population initiale.
• Si µ est légèrement plus grand que 3,54, la population finit par osciller entre huit valeurs, puis 16, 32, etc. L’intervalle des valeurs de µ conduisant au même nombre d’oscillations décroît rapidement. Le rapport entre deux de ces intervalles consécutifs se rapproche à chaque fois de la constante de Feigenbaum, δ = 4,669…. Aucun de ces comportements ne dépend de la population initiale
• Vers µ = 3,57, le chaos s’installe. Aucune oscillation n’est encore visible et de légères variations de la population initiale conduisent à des résultats radicalement différents.
• La plupart des valeurs au-delà de 3,57 présentent un caractère chaotique, mais il existe quelques valeurs isolées de µ avec un comportement qui ne l’est pas. Par exemple vers 3,82, un petit intervalle de valeurs de µ présente une oscillation entre trois valeurs et pour µ légèrement plus grand, entre six valeurs, puis douze, etc. D’autres intervalles offrent des oscillations entre 5 valeurs, etc. Toutes les périodes d’oscillation sont présentes, là encore indépendamment de la population initiale.
• Les périodes d'oscillation précédemment décrites répondent à la règle suivante. Considérons l'ordre de Charkovski défini sur les entiers strictement positifs de la façon suivante :

$3 \;\triangleleft\; 5 \;\triangleleft\; 7 \;\triangleleft\; \ldots \;\triangleleft\; 2\times 3 \;\triangleleft\; 2\times 5 \;\triangleleft\; 2\times 7 \;\triangleleft\; \ldots \;\triangleleft\; 2^n\times 3 \;\triangleleft\; 2^n\times 5 \;\triangleleft\; 2^n\times 7 \;\triangleleft\; \ldots$

$\;\triangleleft\; 2^{n+1}\times 3 \;\triangleleft\; 2^{n+1}\times 5 \;\triangleleft\; \ldots \;\triangleleft\; 2^n \;\triangleleft\; 2^{n-1} \;\triangleleft\; \ldots \;\triangleleft\; 2^2 \;\triangleleft\; 2 \;\triangleleft\; 1$

Autrement dit, on place d'abord les impairs à partir de 3 par ordre croissant, puis les impairs multipliés par 2, puis par 4, etc. et on termine par les puissances de 2 par ordre décroissant. Si une valeur du paramètre µ correspond à une période d'oscillation n, alors tous entiers succédant à n dans l'ordre de Charkovski correspondent à des périodes d'oscillation déjà apparues pour des valeurs du paramètre inférieures à µ. Ainsi, puisque µ = 3,82 correspond à une période 3, toutes les périodes d'oscillation possibles sont déjà apparues pour des valeurs de µ entre 0 et 3,82.

• Au-delà de µ=4, la population quitte l’intervalle [0;1] et diverge quasiment pour toutes les valeurs initiales.

Un diagramme de bifurcation permet de résumer tout cela :

L'axe horizontal porte les valeurs du paramètre µ (noté r), tandis que l'axe vertical montre les valeurs limites possibles.

Commentaires

Quelques raisonnements simples et quelques graphiques permettent d'éclairer partiellement les résultats qui précèdent.

Graphiques

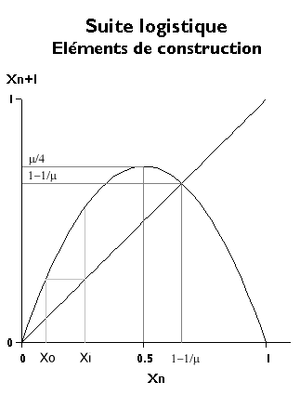
L'évolution de la suite logistique peut être représentée dans le plan (x_n, x_n+1).

L'équation de base représente une parabole qui passe par les points d'abscisses 0 et 1 sur l'axe horizontal. Pour que les valeurs de x_n+1 ne deviennent pas négatives, il faut ne retenir que l'arc compris entre ces deux points ; celui-ci présente, pour x_n = ½, un maximum de valeur μ/4. Cette valeur doit aussi être comprise entre 0 et 1, d'où μ < 4.

Si la suite converge, sa limite satisfait l'équation x_n+1 = x_n. Cette limite éventuelle, notée x, est solution de l'équation du second degré

$x = \mu x(1-x)\,$

et peut donc prendre l'une ou l'autre des valeurs

$x = 0\ x = {{\mu - 1} \over \mu}$

Pour décrire le comportement de la suite, il faut partir d'une abscisse x₀, déterminer sur la parabole la valeur x₁ qui est alors transformée en une nouvelle abscisse en passant par la bissectrice x_n+1 = x_n et répéter ces deux opérations.

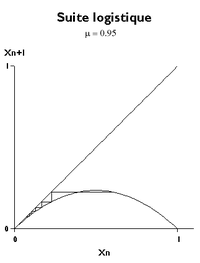
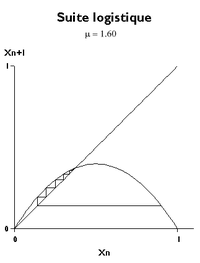
Domaines de convergence

Pour certaines valeurs du paramètre μ, la suite se comporte comme une suite classique et converge vers l'une des deux limites possibles. L'équation de base peut se réécrire sous la forme

${x_{n+1}\over x_n} = \mu (1-x_n)$

Si $0 \le \mu \le 1$, la suite est majorée par une suite géométrique qui tend vers 0.

Pour voir le comportement vis-à-vis de la seconde limite éventuelle, il suffit d'effectuer le changement de variable x_n = u_n + 1 - 1/μ. La formule devient :

${{u_{n+1}+ 1 - 1/\mu}\over {u_n+ 1 - 1/\mu}} = 1-\mu u_n$

Dans ce cas, la condition de convergence exige que le second membre soit compris entre -1 et + 1 : $1 \le \mu \le 3$.

On vérifie que, si u_n est proche de la limite 1 - 1/μ, alors 1-μ u_n est proche de 2 - μ et u_n tend vers sa limite par valeurs croissantes si μ est inférieur à 2, par valeurs alternées s'il est supérieur à 2.

Bifurcations

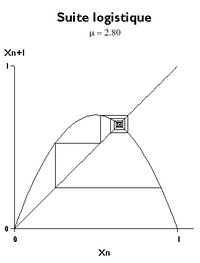
Dans le paragraphe précédent, la formule de récurrence de la forme x_n+1 = f(x_n) a permis d'obtenir les premiers attracteurs en cherchant une limite éventuelle conforme à l'équation x = f(x).

Lorsque μ devient supérieur à 3, il faut chercher une solution à l'équation x = f(f(x)). Cela conduit à une équation du quatrième degré qui possède naturellement les racines déjà connues 0, 1-1/μ – mais ce ne sont plus des attracteurs – et la paire de nouvelles racines

${1 \over 2} ({1 + \mu \over \mu} \pm {1 \over \mu} \sqrt{\mu^2 - 2 \mu - 3})$

Il n'y a plus de convergence : un cycle-limite apparaît. Le résultat de l'itération bascule alternativement de l'une des deux dernières racines à l'autre : u_n+1 =u_n-1 tandis que u_n+2 =u_n. Pour μ = 3.4, les valeurs approchées successives 0.84, 0.45, 0.84, 0.45, 0.84.... apparaissent.

Au-delà de la limite de stabilité de ce cycle, √6 + 1, deux nouvelles bifurcations se produisent, qui dépendent des solutions de x = f(f(f(f(x)))). Pour μ = 3.47, les valeurs successives sont de l'ordre de 0.47, 0.86, 0.40, 0.84, 0.47,...

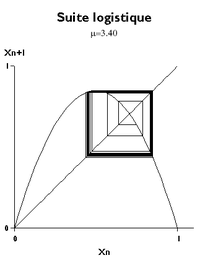
Chaos

De bifurcation en bifurcation, les évolutions deviennent de plus en plus complexes. Le processus aboutit, pour μ > 3.57 environ, à des systèmes qui ne présentent généralement plus d'attracteurs visibles. Les graphiques représentent alors une évolution «chaotique» au sens usuel du terme.

Cependant, dans le langage des mathématiciens, le mot chaos représente une forte sensibilité aux conditions initiales. Les deux graphiques correspondant à μ = 3.9 avec des valeurs initiales u₀ 0.100 et 0.101 montrent que les trajectoires s'éloignent l'une de l'autre jusqu'à devenir rapidement distinctes. Dans un problème concret les conditions initiales ne sont jamais connues exactement : au bout d'un certain temps, un phénomène chaotique est devenu imprévisible alors même que la loi qui le définit est parfaitement déterministe.

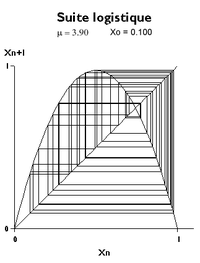
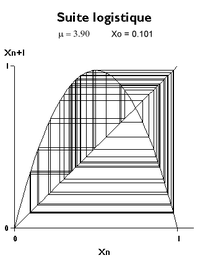
Annexes

Bibliographie

• Alain Hillion, Les Théories mathématiques des populations, PUF, 1986, coll. « Que sais-je », n^o 2258. (ISBN 2-13-039-193-1)

Articles connexes

• Système dynamique
• Théorie du chaos
• Théorie ergodique
• Fractale de Lyapunov
• Autorégulation

Liens externes

• (en) Elmer G. Wiens, The Logistic Map and Chaos
• [PDF] Daniel Perrin, La Suite logistique et le chaos

Notes et références

1. ↑ (en) Why logistic ogive and not autocatalytic curve?