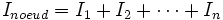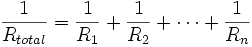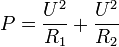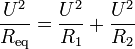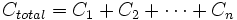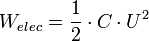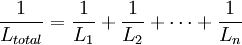- Association en parallèle
-
Circuit en parallèle
 Pour les articles homonymes, voir parallèle.
Pour les articles homonymes, voir parallèle.En électricité, un circuit en parallèle est un circuit électrique dont les branches sont connectées par des nœuds communs. Dans le cas d'un élément à deux bornes, les éléments en parallèle partagent une paire de nœuds, trois pour un élément à trois bornes et ainsi de suite.
Sommaire
Analyse
Dans un circuit en parallèle, les branches sont soumises à la même tension mais le courant n'est pas le même dans chaque branche (sauf cas particuliers). Pour un nœud se divisant en n branches, on a la relation :
où
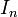 est le courant qui traverse la branche n. Cette relation indique donc que la somme des courants dans chaque branche est égale au courant de nœud. Ces caractéristiques sur la distribution des courants et de la tension dans un circuit parallèle permettent de déduire les valeurs équivalentes d'éléments passifs linéaires combinés en parallèle. Ces formules peuvent être utilisées lors de l'analyse d'un circuit pour simplifier l'obtention de la solution.
est le courant qui traverse la branche n. Cette relation indique donc que la somme des courants dans chaque branche est égale au courant de nœud. Ces caractéristiques sur la distribution des courants et de la tension dans un circuit parallèle permettent de déduire les valeurs équivalentes d'éléments passifs linéaires combinés en parallèle. Ces formules peuvent être utilisées lors de l'analyse d'un circuit pour simplifier l'obtention de la solution.Résistances
Pour une connexion de résistances en parallèle, la résistance totale est égale à :
La résistance totale équivalente est donc plus faible que chacune des résistances individuelles composant le circuit. Dans le cas particulier où toutes les résistances en parallèle sont de mêmes valeurs, la résistance équivalente sera égale à cette valeur divisée par le nombre d'éléments en parallèle.
Démonstration avec les lois de l'électrocinétique
Cette équation peut être démontrée en se basant sur les propriétés du circuit :
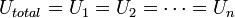
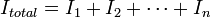
En utilisant la loi d'Ohm et les deux énoncés ci-dessus on peut écrire :
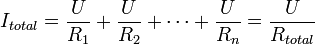
Après simplification par U :Démonstration par la conservation de la puissance
Une démonstration rapide de cette relation peut être faite à partir de considérations énergétiques :
Soit deux résistances :
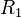 et
et 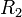 , en parallèle et alimentées par une source de tension. La puissance consommée par cet ensemble est égale à la somme des puissances consommées par chacune des résistance, soit :
, en parallèle et alimentées par une source de tension. La puissance consommée par cet ensemble est égale à la somme des puissances consommées par chacune des résistance, soit :avec
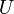 la valeur efficace de la tension aux bornes de ces résistances.
la valeur efficace de la tension aux bornes de ces résistances.La résistance équivalente doit consommer une puissance identique à cet ensemble, d'où :
En simplifiant, on retrouve la formule d'association de résistances en parallèle.
Condensateur
Contrairement au cas des résistances, les condensateurs lorsqu'ils sont placés en parallèle ont une capacité équivalente qui s'exprime comme suit :
La capacité totale est donc la somme de celles de tous les condensateurs formant le circuit parallèle.
Comme pour les résistances cette relation peut être démontrée par des considérations énergétiques. L'énergie stockée dans un condensateur de capacité C et soumis à une tension U étant égale à :
Le condensateur équivalent doit être en mesure de stocker la même énergie que l'ensemble auquel il se substitue quand il est soumis à la même tension.
Inductance
Les inductances comme les résistances ont une valeur totale équivalente plus faible que chacun des éléments individuels. La relation est comme suit :
Bibliographie
- (en) James W. Nilsson, Susan A. Riedel, Introductory Circuits for Electrical and Computer Engineering, Prentice Hall, New Jersey, 2002, (ISBN 0130198552)
Articles connexes
- Portail de l’électricité et de l’électronique
Catégorie : Circuit électrique
Wikimedia Foundation. 2010.