- Probleme du voyageur de commerce
-
Problème du voyageur de commerce
Le problème du voyageur de commerce consiste, étant donné un ensemble de villes séparées par des distances données, à trouver le plus court chemin qui relie toutes les villes. C'est un problème NP-complet.
Sommaire
Approche simplifiée
L'énoncé du problème du voyageur de commerce est le suivant : étant donné n points (des « villes ») et les distances séparant chaque point, trouver un chemin de longueur totale minimale qui passe exactement une fois par chaque point et revienne au point de départ.
Ce problème est plus compliqué qu'il n'y paraît ; on ne connaît pas de méthode de résolution permettant d'obtenir des solutions exactes en un temps raisonnable pour de grandes instances (grand nombre de villes) du problème. Pour ces grandes instances, on devra donc souvent se contenter de solutions approchées, car on se retrouve face à une explosion combinatoire : le nombre de chemins possibles passant par 69 villes est déjà un nombre d'une longueur de 100 chiffres. Pour comparaison, un nombre d'une longueur de 80 chiffres permettrait déjà de représenter le nombre d'atomes dans tout l'univers connu !
Ce problème peut servir tel quel à l'optimisation de trajectoires de machines-outils par exemple, pour minimiser le temps total que met une fraiseuse à commande numérique pour percer n points dans une plaque de tôle. Il se posait également pour optimiser la vitesse de tracé d'une structure (en BTP, par exemple) par une table traçante à l'époque où ces périphériques étaient mécaniques, et non électroniques comme aujourd'hui.
Plus généralement, divers problèmes de recherche opérationnelle se ramènent au voyageur de commerce. Un voyageur de commerce peu scrupuleux serait intéressé par le double problème du chemin le plus court (pour son trajet réel) et du chemin le plus long (pour sa note de frais).
Problème détaillé
Voici un énoncé plus formel du problème du voyageur de commerce sous forme constatée de problème de décision.
Données :
- un graphe complet G = (V,A,ω) avec V un ensemble de sommets, A un ensemble d'arêtes et
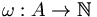 une fonction de coût sur les arcs ;
une fonction de coût sur les arcs ; - un entier
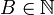
Question :
Existe-t-il un cycle passant une et une seule fois par chaque sommet tel que la somme des coûts des arcs utilisés soit inférieure à B ?
Remarque :
Rien n'interdit au graphe donné en entrée d'être orienté.
Problème symétrique et problème asymétrique
La tsplib[1] distingue[2] deux sous-cas du problème du voyageur de commerce :
Problème du voyageur de commerce symétrique :
Étant donnés un ensemble de n noeuds et de distances pour chaque paire de noeuds, trouver un cycle de longueur minimale qui visite chaque noeud exactement une fois. Pour i et j deux noeuds d'une arrête, la distance de i à j est la même que celle de j à i.
Problème du voyageur de commerce asymétrique :
Étant donnés un ensemble de n noeuds et de distances pour chaque paire de noeuds, trouver un cycle de longueur minimale qui visite chaque noeud exactement une fois. Cette fois-ci la distance entre deux noeuds i et j d'une arrête n'est pas forcément la même qu'on aille de i à j ou bien de j à i.
Approches de résolution
Rigoureusement, résoudre le problème du voyageur de commerce est une tâche difficile : on doit trouver le plus petit cycle hamiltonien (au sens qu'on doit prouver qu'il n'en existe pas de longueur inférieure) dans le graphe d'entrée. Toutefois il arrive qu'on se satisfasse d'une "bonne solution", c'est à dire d'un cycle hamiltonien qui ne soit pas trop loin de la meilleure solution possible.
Résolution exacte
De nombreux travaux de recherche ont concerné le problème du voyageur de commerce. La programmation linéaire permet[3] désormais de résoudre des problèmes de grande taille (à l'échelle d'un pays[4]), moyennant éventuellement un temps de calcul important.
Résolution approchée
Lorsque le temps alloué à la résolution est faible on utilisera plutôt des heuristiques tel que l'Algorithme de Lin-Kernighan[5] et des méta-heuristiques. Toutefois les méthodes heuristiques ne donnent en général aucune preuve justifiant qu'elles obtiennent la meilleure solution, et même si elles peuvent en pratique être très bonnes, en toute généralité elles ne fournissent qu'une solution approchée.
Les algorithmes génétiques peuvent aussi être adaptés au problème du voyageur de commerce. L'idée a été proposée la première fois par John Holland au début des années 1970[6].
Voir aussi
- Heuristique
- Séparation et évaluation
- Problème du sac à dos
- Problème de tournées de véhicules
- Algorithme de colonies de fourmis
Liens externes
- Applet Java illustrant le problème du voyageur de commerce : http://magnin.plil.net/anciensite/coursag/voyageur/voyageur.html
- La tsplib, une librairie fournissant des instances du problème http://www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/
- concorde, un logiciel capable de résoudre des instances du problème http://www.tsp.gatech.edu/concorde/index.html
- un applet utilisant l'api de google maps résolvant des instances du problème http://www.tsp.gatech.edu/maps/index.html
Références
- ↑ bibliothèque fournissant une série d'instances pour le problème du voyageur de commerce (voir dans les liens externes)
- ↑ entre autres!
- ↑ en général par le biais de la méthode du branch and cut
- ↑ Voir par exemple le site de l'université Georgia Tech
- ↑ S. Lin and B. W. Kernighan (1973). An Effective Heuristic Algorithm for the Traveling-Salesman Problem. Operations Res. 21, 498-516.
- ↑ * J. H. Holland: Adaptation In Natural And Artificial Systems, University of Michigan Press (1975)
- Portail de l’informatique
- Portail des mathématiques
Catégories : Théorie des graphes | Problème NP-complet - un graphe complet G = (V,A,ω) avec V un ensemble de sommets, A un ensemble d'arêtes et
Wikimedia Foundation. 2010.

