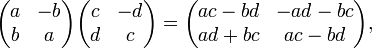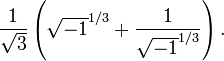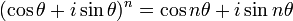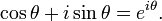- Arithmétique complexe
-
Nombre complexe
 Pour les articles homonymes, voir complexe.
Pour les articles homonymes, voir complexe.Les nombres complexes forment une extension de l'ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels. Les nombres complexes furent introduits au XVIe siècle par les mathématiciens italiens Jérôme Cardan, Raphaël Bombelli, Nicolo Fontana, dit Tartaglia, et Ludovico Ferrari afin d'exprimer les solutions des équations du troisième degré en toute généralité par les formules de Cardan, en utilisant notamment des nombres de carré négatif, ainsi que les solutions des équations du quatrième degré (méthode de Ferrari).
L'ensemble des sommes et produits de nombres réels et du nombre imaginaire i (les nombres de la forme a + i.b) satisfait les propriétés d'une structure de corps commutatif qui contient le corps des réels. Il est appelé corps des nombres complexes et se note
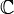 . Il est muni de l'application module qui généralise la valeur absolue des nombres réels mais ne peut pas être ordonné totalement de façon compatible avec sa structure de corps.
. Il est muni de l'application module qui généralise la valeur absolue des nombres réels mais ne peut pas être ordonné totalement de façon compatible avec sa structure de corps.Ce n'est qu'à partir du XIXe siècle que se développe l'aspect géométrique des nombres complexes, vus comme des éléments ou des transformations du plan, sous l'impulsion de l'abbé Buée et de Jean-Robert Argand (plan d'Argand), puis avec les travaux de Gauss et de Cauchy.
En algèbre, le théorème de d'Alembert-Gauss identifie le degré d'un polynôme complexe non nul au nombre de ses racines comptées avec leur ordre de multiplicité. Le corps des nombres complexes est donc algébriquement clos.
En analyse, l'exponentielle complexe permet de simplifier l'étude des séries de Fourier puis de définir la transformée de Fourier. La branche de l'analyse complexe concerne l'étude des fonctions dérivables au sens complexe, appelées fonctions holomorphes.
En physique, les nombres complexes sont utilisés pour décrire le comportement d'oscillateurs électriques ou les phénomènes ondulatoires en électromagnétisme (Re(eiωt) représentant une onde). L'ensemble de Mandelbrot (en noir), illustration d'un système dynamique sur le plan complexe
L'ensemble de Mandelbrot (en noir), illustration d'un système dynamique sur le plan complexe
Sommaire
Description
 Représentation d'un nombre complexe dans l'espace à deux dimensions [en rouge], sous forme cartésienne [en bleu] (avec deux nombres réels) et sous forme polaire [en vert] (avec une longueur et un angle).
Représentation d'un nombre complexe dans l'espace à deux dimensions [en rouge], sous forme cartésienne [en bleu] (avec deux nombres réels) et sous forme polaire [en vert] (avec une longueur et un angle).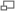
Notations des nombres complexes
Les nombres complexes, notés habituellement z, peuvent ainsi être présentés de plusieurs manières :
- forme cartésienne,
- algébrique :
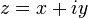
- ou vectorielle :

- algébrique :
- forme en coordonnées polaires :
- géométrique
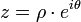
- ou vectorielle :
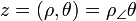
- ou trigonométrique :
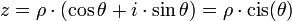
- géométrique
Forme cartésienne
Un nombre complexe
 se présente en général en coordonnées cartésiennes, comme une somme
se présente en général en coordonnées cartésiennes, comme une somme 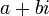 , où a et b sont des nombres réels quelconques et
, où a et b sont des nombres réels quelconques et  (l’unité imaginaire) est un nombre particulier tel que
(l’unité imaginaire) est un nombre particulier tel que 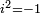 .
.
Le réel a est appelé partie réelle de z et se note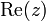 ou
ou  , le réel b est sa partie imaginaire et se note
, le réel b est sa partie imaginaire et se note 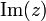 ou
ou 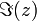 .
.
Deux nombres complexes sont égaux si et seulement s'ils ont la même partie réelle et la même partie imaginaire.Un nombre complexe z est dit imaginaire pur ou totalement imaginaire si sa partie réelle est nulle, dans ce cas il s'écrit sous la forme z = bi. Un nombre complexe dont la partie imaginaire vaut 0 est assimilé à un nombre réel.
Le nombre réel 0 est le seul qui soit à la fois réel et imaginaire pur, mais la plupart des nombres complexes ne sont ni réels ni imaginaires purs.L'addition et la multiplication sur les nombres complexes ont les mêmes propriétés d'associativité, de commutativité et de distributivité que sur les nombres réels. Les règles de calcul s'écrivent donc :
-
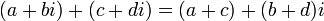 ;
;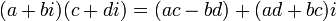 .
.
En particulier, cette formule permet d'obtenir l'égalité suivante :
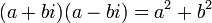 .
.Puisque la somme a2+b2 de deux carrés de nombres réels est un nombre réel strictement positif (sauf si a = b = 0), il existe un inverse à tout nombre complexe non nul avec l'égalité :
Cette fraction fait apparaître deux expressions importantes pour le nombre complexe
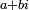 :
:L'application de conjugaison est un automorphisme involutif :
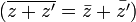 ,
,  et
et 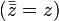 .
.
L'application module est une valeur absolue car elle est strictement positive en dehors de 0, sous-additive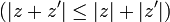 et multiplicative
et multiplicative 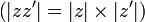 .
.Les réels sont les seuls nombres complexes qui sont égaux à leur conjugué. Les réels positifs sont les seuls complexes égaux à leur module.
Le nombre 0 est le seul nombre complexe dont le module vaut 0.Forme polaire
Plan complexe
Dans un plan affine
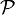 muni d'un repère orthonormé
muni d'un repère orthonormé 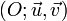 , l'image d'un nombre complexe
, l'image d'un nombre complexe  est le point M de coordonnées (a,b), son image vectorielle est le vecteur
est le point M de coordonnées (a,b), son image vectorielle est le vecteur  . Le nombre z est appelé affixe du point M ou du vecteur
. Le nombre z est appelé affixe du point M ou du vecteur  (affixe est féminin : une affixe).
(affixe est féminin : une affixe).Le module
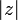 est alors la longueur du segment
est alors la longueur du segment ![\,\ [OM]](/pictures/frwiki/53/5b716a48b43aa6b03064208c731a630b.png) .
.
Si z est différent de 0, son image est distincte de l'origine O du repère. On appelle alors argument de z et on note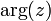 n'importe quelle mesure
n'importe quelle mesure 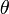 de l'angle
de l'angle  , bien définie à un multiple de 2π près.
, bien définie à un multiple de 2π près.Par exemple, les réels strictement positifs ont un argument multiple de 2π, les réels strictement négatifs ont pour argument un multiple impair de π.
Les imaginaires purs non nuls ont un argument congru à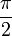 ou
ou 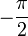 modulo 2π, selon le signe de leur partie imaginaire.
modulo 2π, selon le signe de leur partie imaginaire.Le plan
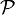 , muni de son repère orthonormé et des actions des nombres complexes par addition et multiplication, est appelé plan complexe. Puisque tous les plans complexes sont canoniquement isomorphes, on parle du plan complexe sans préciser davantage.
, muni de son repère orthonormé et des actions des nombres complexes par addition et multiplication, est appelé plan complexe. Puisque tous les plans complexes sont canoniquement isomorphes, on parle du plan complexe sans préciser davantage.Coordonnées polaires
Le module et l'argument d'un nombre complexe correspondent aux coordonnées polaires (r,θ) de son image dans le plan complexe. En écrivant les coordonnées cartésiennes à partir des coordonnées polaires, tout nombre complexe non nul peut donc s'écrire sous une forme trigonométrique
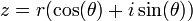 avec
avec 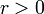 .
.La formule d'Euler
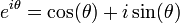 permet de compacter cette écriture sous une forme exponentielle
permet de compacter cette écriture sous une forme exponentielle 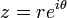 .
.
Le conjugué s'écrit alors simplement .
.Cette écriture est en outre adaptée au calcul du produit de deux nombres complexes du fait des propriétés multiplicatives de la fonction exponentielle :
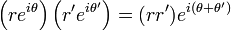 ,
,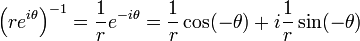 .
.
Interprétation géométrique des opérations
Soit z et z' deux nombres complexes d'images respectives M et M'.
- L'image
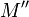 de la somme
de la somme  est définie par la relation
est définie par la relation 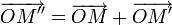 .
.
L'action d'un nombre complexe par addition s'interprète géométriquement comme une translation selon le vecteur image. - Soit λ un nombre réel, l'image M1 du produit
 est défini par la relation
est défini par la relation 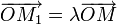 .
.
L'action du nombre réel λ par multiplication scalaire s'interprète géométriquement comme une homothétie de centre O et de rapport λ sur le plan complexe. - Si z est de module 1 et d'argument θ, l'image
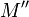 du produit
du produit 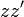 est définie par les relations de longueurs
est définie par les relations de longueurs 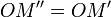 et d'angles
et d'angles 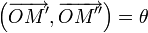 .
.
L'action d'un nombre complexe de module 1 par multiplication s'interprète géométriquement comme une rotation de centre l'origine et d'angle l'argument. - Par composition d'une homothétie et d'une rotation, l'action d'un nombre complexe z non nul par multiplication s'interprète géométriquement comme une similitude directe de centre l'origine, de rapport
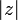 et d'angle
et d'angle 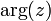 .
. - L'image du conjugué
 de
de 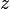 est le symétrique de M par rapport à l'axe des abscisses.
est le symétrique de M par rapport à l'axe des abscisses. - L'image de l'inverse
 de
de 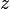 est l'image de M par l'inversion par rapport au cercle unité, composée avec la symétrie par rapport à l'axe des abscisses.
est l'image de M par l'inversion par rapport au cercle unité, composée avec la symétrie par rapport à l'axe des abscisses.
Construction
Article détaillé : Construction des nombres complexes.Il existe plusieurs manières courantes de construire le corps des nombres complexes à partir de l'ensemble des nombres réels et de ses opérations arithmétiques élémentaires. Outre que les objets ainsi définis sont tous isomorphes, les constructions présentées ci-après mettent en lumière trois caractéristiques importantes :
- Le corps des réels est clairement identifié comme un sous-ensemble du corps des complexes et les opérations d'addition et de multiplication sont préservées dans la nouvelle structure. Le nombre réel 1 reste neutre pour la multiplication.
- Il existe un nombre complexe
 canoniquement choisi dont le carré vaut − 1, bien que son opposé vérifie aussi cette propriété.
canoniquement choisi dont le carré vaut − 1, bien que son opposé vérifie aussi cette propriété. - Deux paramètres réels sont nécessaires et suffisants pour décrire tous les nombres complexes, ce qui souligne la structure d'espace vectoriel réel de dimension 2 avec une base canonique.
Vecteur du plan euclidien
On peut définir un nombre complexe comme un vecteur du plan
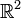 muni de sa base canonique.
muni de sa base canonique.Chaque nombre complexe est donc représenté par un couple (a,b) de nombre réels.
L'addition correspond à celle des vecteurs, c'est-à-dire l'addition des coordonnées terme à terme :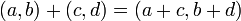 .
.
La multiplication est définie « arbitrairement » par :
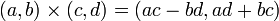 .
.
L'ensemble des réels s'identifie avec la droite
 et l'élément
et l'élément  est le deuxième vecteur de base (0,1). Le module d'un nombre complexe correspond enfin à la norme euclidienne du vecteur associé et l'argument est une mesure de l'angle formé par le vecteur associé avec le premier vecteur de base.
est le deuxième vecteur de base (0,1). Le module d'un nombre complexe correspond enfin à la norme euclidienne du vecteur associé et l'argument est une mesure de l'angle formé par le vecteur associé avec le premier vecteur de base.Cette définition présente l'avantage de la simplicité, puisqu'elle exige peu de prérequis mathématiques. Elle est en outre adaptée à la représentation géométrique des nombres complexes.
Matrice de similitude
Il est intéressant de définir un nombre complexe comme une matrice de similitude directe
 à coefficients réels, car les opérations matricielles induisent précisément la structure algébrique voulue. En outre, le module et l'argument deviennent respectivement le rapport et une mesure de l'angle de la similitude.
à coefficients réels, car les opérations matricielles induisent précisément la structure algébrique voulue. En outre, le module et l'argument deviennent respectivement le rapport et une mesure de l'angle de la similitude.
Il faut cependant vérifier que l'ensemble de ces matrices est stable par produit :ce qui justifie au passage la commutativité du produit et assure l'isomorphisme entre cette structure et celle définie précédemment.
L'ensemble des réels s'identifie alors à l'ensemble des matrices diagonales de la forme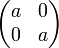 , l'unité étant représentée par la matrice identité. L'élément
, l'unité étant représentée par la matrice identité. L'élément  désigne classiquement la matrice
désigne classiquement la matrice 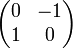 .
.
Le déterminant correspond au carré du module, ce qui entraîne que toutes les éléments non nuls sont inversibles et la méthode des cofacteurs démontre la stabilité par inverse.Ce point de vue fournit une construction naturelle qui peut être adaptée pour obtenir l'algèbre réelle des quaternions. Il donne en outre une interprétation géométrique de la multiplication des nombres complexes comme composition de similitudes du plan. La conjugaison est enfin représentée par la transposition de matrices.
Classe d'équivalence de polynômes
Un nombre complexe peut enfin être vu comme un polynôme réel d'indéterminée i, où le carré i2 est identifié avec le polynôme constant de valeur − 1, donc avec les identifications i3 = − i ; i4 = 1…
Formellement, cela revient à assimiler l'ensemble des nombres complexes à l'espace quotient![\R[X]/(X^2 + 1)](/pictures/frwiki/97/a9dc8e69251c016fa9403836e5f573b4.png) , dans lequel deux polynômes appartiennent à la même classe d'équivalence si et seulement s'ils ont le même reste de division euclidienne par X2 + 1.
, dans lequel deux polynômes appartiennent à la même classe d'équivalence si et seulement s'ils ont le même reste de division euclidienne par X2 + 1.
Le caractère irréductible du polynôme X2 + 1 assure directement la structure de corps. Les réels sont représentés par les polynômes constants et le degré 2 du polynôme diviseur est la dimension de l'ensemble comme espace vectoriel réel.Cette conception très sophistiquée en apparence est peut-être celle qui décrit le mieux l'invention des nombres complexes, loin de la géométrie, à partir d'un seul générateur algébrique et d'une seule relation. Le formalisme (plus récent) du quotient d'un anneau euclidien (ici l'anneau des polynômes réels à une indéterminée) par un de ses idéaux irréductibles est à la base de la construction des extensions algébriques de corps.
Structure du corps des complexes
Les racines carrées d'un nombre complexe s'écrivent facilement lorsque celui-ci est sous forme trigonométrique : celles de z = reiθ sont
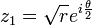 et
et 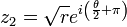 et sont opposées l'une de l'autre.
et sont opposées l'une de l'autre.
L'existence de deux racines carrées, dans le corps des nombres complexes, pour tout nombre complexe non nul (y compris pour tout réel strictement négatif) est une propriété qui n'est pas vérifiée par restriction au corps des réels, puisqu'aucun réel strictement négatif ne peut s'obtenir comme le carré d'un nombre réel.Article détaillé : Racine de nombre complexe.Plus généralement, tout polynôme à coefficients complexes (donc, en particulier, tout polynôme à coefficients entiers ou rationnels), non constant, admet au moins une racine (ce qui implique qu’il en admet autant que son degré, en les comptant avec leurs multiplicités). On dit que le corps des complexes est algébriquement clos. Ce résultat est connu en France sous le nom de Théorème de d'Alembert-Gauss, dans d'autres pays sous le nom de théorème fondamental de l'algèbre.
Article détaillé : Théorème de d'Alembert-Gauss.En fait, le corps des complexes est la clôture algébrique du corps des réels, c'est-à-dire le plus petit corps qui contienne le corps des réels et qui soit algébriquement clos. Du point de vue de la théorie de Galois, on peut considérer les automorphismes du corps des complexes : l'identité et la conjugaison sont ses seuls automorphismes continus (on peut remplacer l'hypothèse « continu » par, au choix, « mesurable » ou « tel que l'image de tout réel est un réel »). En supposant l'axiome du choix on peut construire des automorphismes « exotiques » de ce corps: voir automorphismes de corps non continus de C.
Développements en mathématiques
Analyse complexe
Article détaillé : Analyse complexe.Les nombres complexes ont initialement été conçus pour répondre à un problème algébrique. Cependant, étendre les définitions de l'analyse au champ des nombres complexes s'avère tout aussi fécond. Par exemple la définition usuelle de la dérivée :
 (avec usage de la multiplication et de la soustraction complexes) permet d'obtenir une nouvelle notion de fonction dérivable, de variable complexe à valeurs complexes appelée fonction holomorphe. Cette notion s'avère plus restrictive que son pendant réel, notamment, toute fonction holomorphe voit sa dérivée être holomorphe, et même, toute fonction holomorphe est analytique, c'est-à-dire admet un développement en série entière en chacun des points de son domaine d'holomorphie.
(avec usage de la multiplication et de la soustraction complexes) permet d'obtenir une nouvelle notion de fonction dérivable, de variable complexe à valeurs complexes appelée fonction holomorphe. Cette notion s'avère plus restrictive que son pendant réel, notamment, toute fonction holomorphe voit sa dérivée être holomorphe, et même, toute fonction holomorphe est analytique, c'est-à-dire admet un développement en série entière en chacun des points de son domaine d'holomorphie.En théorie de l'intégration, en utilisant la notion d'intégrale le long d'un chemin, on obtient le théorème intégral de Cauchy, qui assure que l'intégrale d'une fonction holomorphe, sur un domaine vérifiant certaines propriétés topologiques, le long d'un chemin fermé, est nulle. Cette propriété cruciale permet d'obtenir la notion de primitive d'une fonction holomorphe, toujours sur un domaine adapté. Certaines de ces conditions topologiques peuvent être abandonnées, grâce à la notion de point singulier, aboutissant au théorème des résidus.
Dynamique holomorphe
Article détaillé : Dynamique holomorphe.La dynamique holomorphe à une variable consiste en l'étude du comportement des itérés d'une fonction holomorphe f définie sur une surface de Riemann. On distingue deux types de points sur ces surfaces : ceux où la famille des itérés est normale, en ces points la dynamique est assez simple (bassins d'attractions de cycles de points périodiques), dont l'ensemble est appelé ensemble de Fatou de f, puis ceux où le comportement est chaotique et dont l'ensemble est appelé ensemble de Julia de f.
Les propriétés de ces itérés sont particulièrement bien connues dans le cadre de la sphère de Riemann : classification complète des composantes connexes de l'ensemble de Fatou selon les propriétés de f, propriétés de l'ensemble de Julia, étude des espaces à paramètres de polynômes...
On étudie aussi la dynamique holomorphe à plusieurs variables, par exemple dans les espaces projectifs complexes où apparaissent de nouvelles difficultés par rapport à une variable telles que la présence d'ensembles de points où f n'est pas définie.
Équations différentielles dans le champ complexe
L'étude des équations différentielles holomorphes a les mêmes résultats de base que celle des équations sur des fonctions de variable réelle, et notamment le théorème de Cauchy-Lipschitz, qui donne l'existence et l'unicité d'une solution à un problème de Cauchy ; ou les résultats d'algèbre linéaire sur les espaces de solutions des équations différentielles linéaires.
Cependant, l'étude des équations aux points singuliers est nettement plus féconde que les simples études de raccord du cas réel : la topologie du plan complexe au voisinage d'un point singulier fait qu'il y a une infinité de manière de l'approcher, et l'étude des raccords des solutions obtenues avec toutes les méthodes d'approche amène à la notion de monodromie. Cette notion est ensuite utilisée dans un cadre plus général : la théorie de Galois différentielle.
Analyse de Fourier
Article détaillé : Analyse harmonique.Nombres hypercomplexes
Article détaillé : Nombre hypercomplexe.En topologie
- En identifiant l'espace vectoriel
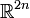 avec l'espace vectoriel
avec l'espace vectoriel 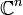 , la multiplication par
, la multiplication par  définit une application sans point fixe sur les sphères de dimension impaire.
définit une application sans point fixe sur les sphères de dimension impaire. - L'adjonction d'un point « à l'infini » au plan complexe définit la sphère de Riemann homéomorphe à la sphère usuelle S2, qui peut être vue comme le premier espace projectif complexe.
La projection de la sphère S3, vue comme sphère unité de l'espace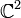 , sur la sphère de Riemann par quotient de l'action du cercle unité S1 constitue alors la fibration de Hopf.
, sur la sphère de Riemann par quotient de l'action du cercle unité S1 constitue alors la fibration de Hopf. - Les espaces projectifs complexes de dimension paire engendrent rationnellement l'anneau de cobordisme orienté[1].
Emplois en physique et ingénierie
Représentation des phénomènes périodiques et analyse de Fourier
La forme trigonométrique a permis de simplifier la modélisation et l’écriture de nombreux phénomènes, par exemple les phénomènes ondulatoires notamment à propos des ondes électromagnétiques, ou en électronique et plus précisément dans le domaine de l'analyse électronique des circuits contenant des auto-inductances (selfs ou bobines) notées L, des capacités notées C et des résistances notées R (exemples, R+jLw ou R-j/Cw). Dans le domaine de l'électronique, le i représentant l'imaginaire en mathématiques, se note j. On peut tracer alors le diagramme de Fresnel et ce, quelle que soit l'expression.
En fait, on se sert du fait que
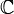 contient
contient  pour simplifier les écritures. En effet, si l’on doit écrire qu’un paramètre vaut r cos(θ), il faut deux réels, r et θ. Mais avec des complexes, il suffit d’UN nombre, ce qui est bien plus simple.
pour simplifier les écritures. En effet, si l’on doit écrire qu’un paramètre vaut r cos(θ), il faut deux réels, r et θ. Mais avec des complexes, il suffit d’UN nombre, ce qui est bien plus simple.En électromagnétisme toujours, mais dans un contexte différent, on peut écrire le champ électromagnétique comme une combinaison complexe du champ électrique et du champ magnétique. Pur artifice de calcul, on peut associer l’un ou l’autre de ces champs à la partie « imaginaire » du champ complexe obtenu : cela simplifie grandement les opérations.
On utilise également les complexes pour l’analyse de Fourier, très utilisée dans de nombreux domaines, comme le traitement du signal.
Mécanique des fluides dans le plan
En mécanique des fluides (hydro/aérodynamique), on fait apparaître des potentiels et des vitesses complexes. En effet, pour un écoulement à deux dimensions, on peut décomposer la vitesse du fluide en vx et vy. Or, on montre que :
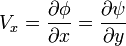
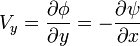
Satisfaire à ces conditions (conditions de Cauchy-Riemann) équivaut à dire qu’il existe une fonction analytique telle que
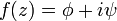 où
où 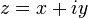
Ceci permet encore d’écrire :
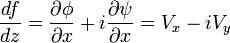
On appelle f(z) le potentiel complexe, et sa dérivée par rapport à z, la vitesse complexe. Grâce à cette fonction, on obtient directement le module de la vitesse, et sa direction (en prenant la forme trigonométrique). Surtout, on peut modéliser simplement un écoulement autour d’un obstacle, d’une manière simple et compacte. La fonction ψ doit être constante le long du profil de cet obstacle, ce qui permet une résolution simple de f, grâce à des résultats simples d’analyse complexe.
Mécanique quantique
Autre simplification pour physiciens : la mécanique quantique nécessite les nombres complexes. Les fonctions d’ondes quantiques sont ainsi toutes complexes (voir Postulats de la mécanique quantique). Dans ce cas, toutefois, il est possible (selon des théories non quantiques) que cela corresponde à la structure réelle de l’univers : non plus à 4 dimensions (espace-temps), mais de 5 et plus - dans certaines théories jusqu’à 11 - aux échelles quantiques (petites). Malgré notre perception (adaptée aux échelles plus grandes), la dimension imaginaire pourrait donc fort bien correspondre aussi à une « réalité physique » et non pas représenter seulement une commodité d’écriture.
Si tant est d’ailleurs qu’on ait lieu d’établir une différence, car on remarque que les notations efficaces pour engendrer des objets le sont tout autant pour les décrire avec précision ensuite (voir Fractale, Complexité de Kolmogorov, Compression, Entropie de Shannon et même Notation neumatique en musique).
Historique
La première allusion aux racines des nombres négatifs apparaît avec les travaux du mathématicien grec et inventeur Héron d'Alexandrie au Ier siècle av. J.-C., quand il s'intéresse au volume du tronc impossible d'une pyramide, et ce malgré le fait qu'à l'époque hellénistique les nombres négatifs soient inconcevables.
Les nombres complexes apparaissent plus clairement au XVIe siècle, quand est établie une formule de calcul pour les racines polynomiales des équations cubiques et quartiques polynomiales par les mathématiciens italiens Niccolo Fontana Tartaglia et Gerolamo Cardano. On réalise très tôt que ces formules, même si l'on ne s'intéresse qu'aux solutions réelles, nécessitent parfois de manipuler la racine carrée de nombres négatifs. Par exemple, la formule cubique de Tartaglia donne la solution suivante à l'équation x³ − x = 0:
Le calcul formel avec les nombres complexes montre que l'équation z³ = i a pour solution −i,
 et
et 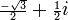 . En substituant ces résultats dans
. En substituant ces résultats dans 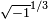 et en simplifiant, on obtient 0, 1 et −1 comme solutions de x³ − x = 0.
et en simplifiant, on obtient 0, 1 et −1 comme solutions de x³ − x = 0.Ces méthodes de calcul sont obtenues alors que la notion de nombre négatif n'est pas encore validée à l'époque. L'appellation nombre imaginaire pour ces quantités est introduit, tant leur réalité est contestable, par René Descartes en 1637. Une source de confusion supplémentaire réside dans le fait que l’équation
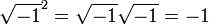 combinée avec l'identité algébrique
combinée avec l'identité algébrique 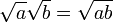 (valide avec des réels positifs a et b) aboutit au résultat absurde
(valide avec des réels positifs a et b) aboutit au résultat absurde 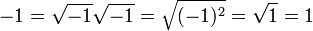 . L’utilisation incorrecte de cette identité (et de l’identité liée
. L’utilisation incorrecte de cette identité (et de l’identité liée 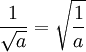 ) dans le cas où à la fois a et b sont négatifs tient notamment Leonhard Euler en échec. C’est cette difficulté qui mène les mathématiciens de l’époque à convenir d’utiliser le symbole spécial i à la place de
) dans le cas où à la fois a et b sont négatifs tient notamment Leonhard Euler en échec. C’est cette difficulté qui mène les mathématiciens de l’époque à convenir d’utiliser le symbole spécial i à la place de 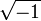 pour se préserver de cette erreur.
pour se préserver de cette erreur.Au XVIIIe siècle, en 1730, Abraham de Moivre énonce la formule bien connue qui porte son nom (formule de De Moivre) :
Peu de temps après, en 1748, Euler donne, quant à lui, la formule suivante (formule d'Euler) :
Ce n'est qu'en 1799 que l'existence des nombres complexes est complètement admise avec l’interprétation géométrique décrite par Caspar Wessel. Plusieurs années après, Carl Friedrich Gauss la redécouvre et la popularise et c'est alors que cette théorie prend un essor considérable. Il a noté cependant que l’idée d’une représentation graphique des nombres complexes est déjà mentionnée, en 1685, dans l’ouvrage de John Wallis De Algebra tractatus.
Un mémoire de Wessel, clair et complet, apparaît dans les minutes de l’Académie de Copenhague en 1799. Il y reconsidère la sphère et fournit une théorie des quaternions à partir de laquelle il développe une théorie complète sur la trigonométrie sphérique. Dans une publication de 1806, l’Abbé Buée reprend l’idée, suggérée par Wallis, que
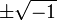 pourrait représenter 1 et -1 sur une ligne perpendiculaire à l’axe réel ; Jean-Robert Argand publie sur le même sujet au même moment. En 1831, Gauss établit une théorie relativement peu connue, et en 1832 publie son mémoire principal sur le sujet. On peut aussi mentionner le petit traité de Mourey (1828), dans lequel les fondements de la théorie des nombres directionnels sont posés. L’acceptation générale de la théorie doit aussi beaucoup aux travaux de Augustin Louis Cauchy et Niels Henrik Abel, ce dernier étant spécialement connu comme le premier à avoir fait, avec succès, un usage massif des nombres complexes.
pourrait représenter 1 et -1 sur une ligne perpendiculaire à l’axe réel ; Jean-Robert Argand publie sur le même sujet au même moment. En 1831, Gauss établit une théorie relativement peu connue, et en 1832 publie son mémoire principal sur le sujet. On peut aussi mentionner le petit traité de Mourey (1828), dans lequel les fondements de la théorie des nombres directionnels sont posés. L’acceptation générale de la théorie doit aussi beaucoup aux travaux de Augustin Louis Cauchy et Niels Henrik Abel, ce dernier étant spécialement connu comme le premier à avoir fait, avec succès, un usage massif des nombres complexes.Les plupart des termes communément utilisés dans la théorie sont dus aux fondateurs :
- Argand appele cosφ + isinφ le facteur direction, et
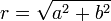 le module ;
le module ; - Cauchy (1828) appelle cosφ + isinφ l'expression réduite ;
- Gauss utilise i pour
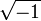 , introduit le terme nombre complexe pour a + bi et appelle a2 + b2 la norme ;
, introduit le terme nombre complexe pour a + bi et appelle a2 + b2 la norme ; - Hankel (1867) appelle cosφ + isinφ coefficient directionnel ;
- Weierstrass, quant à lui, emploie valeur absolue pour module.
Après Cauchy et Gauss suivront nombre de contributeurs. Parmi ceux-ci :
- Kummer (1844) ;
- Kronecker (1845),
- Scheffler (1845, 1851, 1880) ;
- Bellavitis (1835, 1852) ;
- Peacock (1845) ;
- De Morgan (1849) ;
- Möbius à qui l'on doit de nombreuses publications sur les applications géométriques des nombres complexes ;
- Dirichlet pour avoir étendu la théorie des nombres complexes et y incluant les nombres premiers, la notion de congruence, de réciprocité, etc., comme dans le cas des nombres réels.
Un anneau ou un corps est un ensemble de nombres stable par addition, soustraction et multiplication (et division dans le cas d'un corps. Gauss étudie les nombres complexes de la forme a + bi, où a et b sont entiers, ou rationnels. Son élève, Ferdinand Eisenstein, étudie les nombres de la forme a + bω, où ω est une racine complexe de x3 − 1 = 0. D’autres corps, dits cyclotomique, sont obtenus à partir des racines de l’unité xk − 1 = 0 pour k entier positif quelconque. Cette généralisation est largement due à Kummer, qui invente aussi les nombres idéaux.
Enfin, parmi les derniers contributeurs (après 1884) de la théorie générale :
- Weierstrass ;
- Schwarz ;
- Dedekind ;
- Hölder ;
- l'abbé Berloty ;
- Poincaré ;
- Eduard Study ;
- MacFarlane.
Une définition formelle correcte, utilisant des paires de nombres réels, a été donnée au XIXe siècle.
Voir aussi
- Construction des nombres complexes
- Analyse complexe
- Fonction holomorphe
- Racine de nombre complexe
- Trigonométrie complexe
- Nombres complexes fendus
- Sphère de Riemann
- Unité imaginaire
Références
- ↑ J. W. Milnor, J. D. Stasheff, Characteristic classes, Annals of Math. Studies 76, Priceton University Press (1974)
Liens externes
- Nombres complexes
- (histoire des sciences) La représentation dans le plan des nombres complexes, par J.-R. Argand, article (1806) en ligne et commenté sur le site BibNum.
- (en) Moebius Transformations Revealed, Douglas N. Arnold, Jonathan Rogness, Université du Minnesota, film de 2 min 34 (version Youtube)
- Portail des mathématiques
Catégories : Nombre complexe | Nombre hypercomplexe | Analyse complexe - forme cartésienne,
Wikimedia Foundation. 2010.


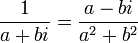
 est aussi un nombre complexe ;
est aussi un nombre complexe ;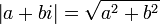 est un nombre réel positif.
est un nombre réel positif.