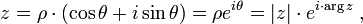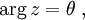Argument D'un Nombre Complexe
- Argument D'un Nombre Complexe
-
Argument d'un nombre complexe
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Argument D'un Nombre Complexe de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Argument d'un nombre complexe — Représentation des valeurs possibles de l argument, avec sa branche principale hachurée en rouge Cet article est un complément de nombre complexe. Un argument d’un nombre complexe non nul z est une mesure (en radians) … Wikipédia en Français
Nombre Complexe — Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels. Les nombres… … Wikipédia en Français
Nombre complexe — Pour les articles homonymes, voir complexe. En mathématiques, les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels … Wikipédia en Français
Racine d'un nombre complexe — Une racine carrée d un nombre complexe z est un nombre complexe w vérifiant w2 = z. Tout nombre complexe a exactement deux racines carrées distinctes, excepté 0, dont 0 est la seule racine carrée. Par exemple, les deux racines carrées de 1 sont i … Wikipédia en Français
argument — [ argymɑ̃ ] n. m. • 1160; lat. argumentum → arguer 1 ♦ Raisonnement destiné à prouver ou à réfuter une proposition, et par ext. Preuve à l appui ou à l encontre d une proposition. ⇒ raisonnement; argumentation, démonstration; preuve, raison.… … Encyclopédie Universelle
Argument (mathématiques) — Argument d un nombre complexe Cet article est un complément de nombre complexe. Un argument d’un nombre complexe non nul d image ponctuelle (dans le plan complexe) est une mesure (en radians) de l’angle : . On a alors� … Wikipédia en Français
Racine De Nombre Complexe — Racine d un nombre complexe Une racine carrée d un nombre complexe z est un nombre complexe w vérifiant w2=z. Tout nombre complexe a exactement deux racines carrées distinctes, excepté 0, dont 0 est la seule racine carrée. Par exemple, les deux… … Wikipédia en Français
Racine de nombre complexe — Racine d un nombre complexe Une racine carrée d un nombre complexe z est un nombre complexe w vérifiant w2=z. Tout nombre complexe a exactement deux racines carrées distinctes, excepté 0, dont 0 est la seule racine carrée. Par exemple, les deux… … Wikipédia en Français
Argument fort — Argument Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Argument — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Argument », sur le Wiktionnaire (dictionnaire universel) En rhétorique, un argument (voir aussi… … Wikipédia en Français
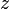 non nul d'image ponctuelle
non nul d'image ponctuelle 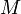 (dans le plan complexe) est une mesure
(dans le plan complexe) est une mesure 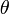 (en radians) de l’angle :
(en radians) de l’angle :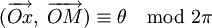 .
.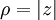 représente le module de
représente le module de 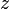 .
.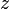 de façon simplifiée par :
de façon simplifiée par :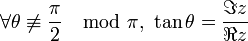 comme en coordonnées polaires et donc :
comme en coordonnées polaires et donc :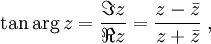 où
où 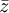 est le conjugué de
est le conjugué de 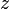 ,
,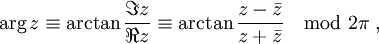 .
. , si z n'est pas un réel négatif, π sinon.
, si z n'est pas un réel négatif, π sinon.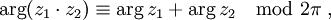 si
si 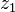 et
et 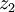 sont des complexes non nuls.
sont des complexes non nuls.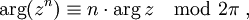 si
si 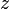 est un complexe non nul et
est un complexe non nul et 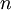 un naturel.
un naturel.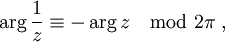 si
si 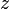 est un complexe non nul.
est un complexe non nul.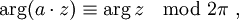 si
si 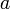 est un réel strictement positif et
est un réel strictement positif et 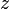 un complexe non nul.
un complexe non nul.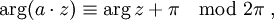 si
si 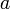 est un réel strictement négatif et
est un réel strictement négatif et 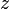 un complexe non nul.
un complexe non nul.