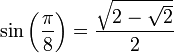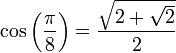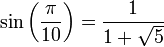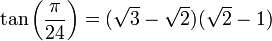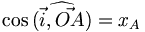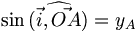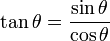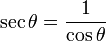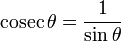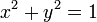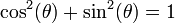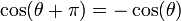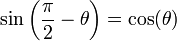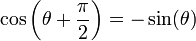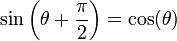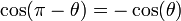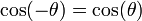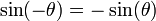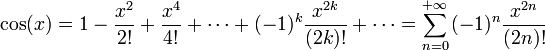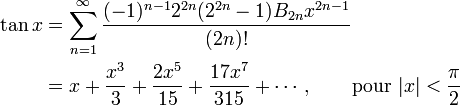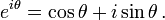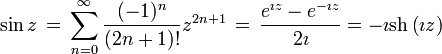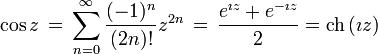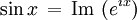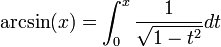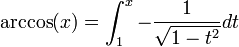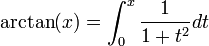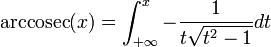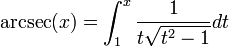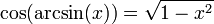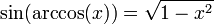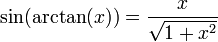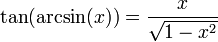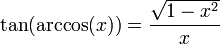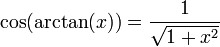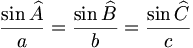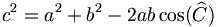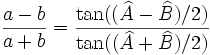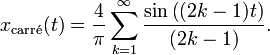- Arcsinus
-
Fonction trigonométrique
En mathématiques, les fonctions trigonométriques sont des fonctions d'angle importantes pour étudier les triangles, les cercles et modéliser des phénomènes périodiques. Les fonctions trigonométriques ne sont rien d'autre que des longueurs relatives à la mesure d'un angle sur le cercle unité, mais elles sont utilisées dans de nombreuses autres applications. Elles sont parfois définies comme rapports de deux longueurs des côtés d'un triangle rectangle contenant l'angle, ou, plus généralement, comme somme d'une série entière.
Chacune de ces trois approches sera présentée ci-dessous. Il y a six fonctions trigonométriques de base :
- sinus (sin) ;
- cosinus (cos) ;
- tangente (tan), noté aussi tang ou tg ;
- sécante (sec), noté aussi séc ;
- cosécante (cosec), noté aussi coséc ou csc ;
- cotangente (cotan), noté aussi cotg ou cot.
Le sinus, le cosinus et la tangente sont de loin les plus utilisées. Plusieurs relations entre ces fonctions sont énumérées à la page des identités trigonométriques.
Sommaire
Lignes trigonométriques
Un triangle quelconque rectiligne (ou sphérique) possède six parties dont trois côtés et trois angles. Toutes ces parties ne sont pas utiles à la construction du triangle, par exemple les seules données de la longueur de deux de ses côtés et de l'angle entre ces côtés permet de compléter le triangle. Mais connaissant seulement les trois angles, il est impossible de retrouver le triangle, puisqu'il existe une infinité de triangles ayant les trois mêmes angles (triangles semblables). En fait il suffit de connaître trois de ces parties dont un côté pour construire un triangle.
Le problème de la détermination avec exactitude des parties manquantes du triangle fut étudié en particulier en Europe à partir du Moyen Âge. Les méthodes géométriques ne donnant, à l'exception des cas simples, que des constructions approximatives et insuffisantes à cause de l'imperfection des instruments utilisés, les recherches s'orientèrent plutôt vers des méthodes numériques afin d'obtenir des constructions avec un degré de précision voulu.
Et l'un des objectifs de la trigonométrie fut donc de donner des méthodes pour calculer toutes les parties d'un triangle, c'est-à-dire pour résoudre un triangle. Pendant longtemps les géomètres cherchèrent en vain des relations entre les angles et les côtés des triangles. Une de leurs plus grandes idées fut de se servir des arcs plutôt que des angles pour effectuer leurs mesures.
Un arc est un arc de cercle décrit de l'un des sommets du triangle comme centre et compris entre les côtés se rapportant au sommet. Ces considérations menèrent tout naturellement les géomètres à remplacer les arcs par les segments de droites dont ils dépendent.
Ces segments s'appellent les lignes trigonométriques. Il s'agit en fait d'un autre vocable pour désigner les fonctions trigonométriques (sin x, cos x, tan x, ...) appelées aussi fonctions circulaires. Des relations entre les côtés et certaines lignes liées aux arcs s'établissent de manière à ce que les lignes puissent être déterminées à partir de certains arcs et réciproquement. Une convention fondamentale oblige alors à ne considérer que les lignes trigonométriques rapportées à des cercles de rayon 1. Ces lignes trigonométriques définissent les fonctions trigonométriques modernes.
Les fonctions trigonométriques mathématiques sont celles qui s'appliquent à des mesures d'angles données en radians. Mais il est encore d'usage de garder les mêmes noms de fonctions pour les autres unités de mesures comme les degrés ou les grades.
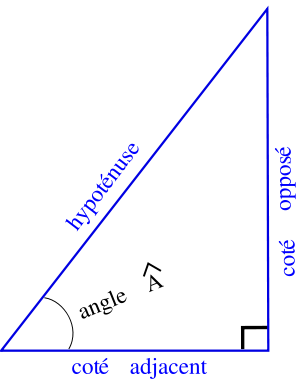
Définitions dans le triangle rectangle
Pour définir les fonctions trigonométriques en un angle Â, considérons un triangle rectangle arbitraire qui contient l'angle Â.
Nous emploierons les noms suivants pour désigner les côtés du triangle rectangle :
- l’hypoténuse est le côté opposé à l'angle droit, une jambe de l'angle  et le coté le plus long du triangle,
- le côté opposé est le côté opposé à l'angle Â, qui nous intéresse,
- le côté adjacent est le côté qui est une jambe de l'angle Â, qui n'est pas l'hypoténuse.
On notera:
- o : la longueur du côté opposé
- a : la longueur du côté adjacent
- h : la longueur de l'hypoténuse
1) Le sinus d'un angle est le rapport de la longueur du côté opposé par la longueur de l'hypoténuse :
- sin(Â) = longueur du côté opposé / longueur de l'hypoténuse = o/h.
Notez que ce rapport ne dépend pas du triangle rectangle particulier choisi, aussi longtemps qu'il contient l'angle Â, puisque tous ces triangles rectangles sont semblables.
2) Le cosinus d'un angle est le rapport de la longueur du côté adjacent par la longueur de l'hypoténuse :
- cos(Â) = longueur de côté adjacent / longueur de l'hypoténuse = a/h.
3) La tangente d'un angle est le rapport de la longueur du côté opposé à la longueur du côté adjacent :
- tan(Â) = longueur du côté opposé / longueur du côté adjacent = o/a.
Les trois fonctions restantes sont définies en utilisant les trois fonctions ci-dessus.
4) La cosécante de  notée cosec(Â) est l'inverse du sinus de Â, 1/sin(Â), c'est-à-dire le rapport de la longueur de l'hypoténuse par la longueur du côté opposé :
- cosec(Â)=longueur de l'hypoténuse / longueur du côté opposé = h/o.
5) La sécante de  notée sec(Â) est l'inverse du cosinus de Â, 1/cos(Â), c'est-à-dire le rapport de la longueur de l'hypoténuse par la longueur du côté adjacent:
- sec(Â)=longueur de l'hypoténuse / longueur du côté adjacent = h/a.
6) La cotangente de  notée cotg(Â) est l'inverse de la tangente de Â, 1/tan(Â), c'est-à-dire le rapport de la longueur du côté adjacent par la longueur du côté opposé:
- cotg(Â)= longueur du côté adjacent / longueur du côté opposé = a/o.
Il existe un moyen mnémotechnique pour apprendre facilement les formules du sinus, du cosinus et de la tangente : CAH;SOH;TOA
- CAH (Cos= Adjacent/Hypotènuse)
- SOH (Sin= Opposé/Hypotènuse)
- TOA (Tan= Opposé/Adjacent)
- Cosadjhyp(cos=adj/hyp)
- Sinopphyp(sin=opp/hyp)
- Tanoppadj(tan=opp/adj)
Valeurs remarquables
Il existe des tables de valeurs des fonctions trigonométriques, mais ces valeurs peuvent également être calculées par une calculatrice. Pour quelques angles simples, les valeurs peuvent être calculées à la main, comme dans les exemples suivants :
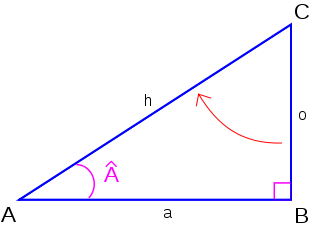
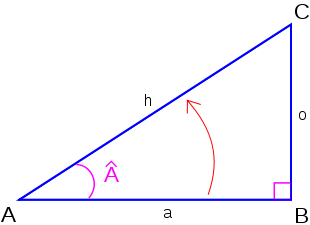
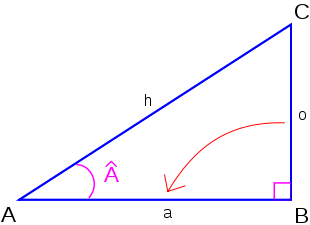
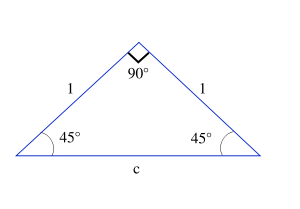
Supposons que l'on ait un triangle rectangle dans lequel les deux angles sont égaux et valant donc 45 degrés (π/4 radians). Puisque les longueurs a et b sont égales, nous pouvons choisir a = b = 1.
Maintenant, on peut déterminer le sinus, le cosinus et la tangente d'un angle de 45 degrés. En utilisant le théorème de Pythagore,
 . Ceci est illustré dans la figure de droite.
. Ceci est illustré dans la figure de droite.Par conséquent,
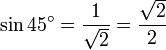 ,
,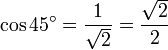 ,
,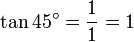
Pour déterminer les valeurs des fonctions trigonométriques pour des angles de 60 degrés (π/3 radians) et de 30 degrés (π/6 radians), nous commençons par considérer un triangle équilatéral de longueur latérale 1. Tous ses angles sont de 60 degrés. En le divisant en deux, nous obtenons un triangle rectangle dont un angle est de 30 degrés. On obtient :
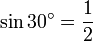 ,
,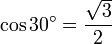 ,
,
et
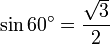 ,
,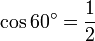 ,
,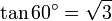 .
.
On peut se souvenir de ces valeurs en construisant la table suivante : en mettant dans l'ordre 0, π/6 (30°), π/4 (45°), π/3 (60°) et π/2 (90°), le sinus prend les valeurs
 , et pour le cosinus, on prend l'ordre inverse.
, et pour le cosinus, on prend l'ordre inverse.Valeurs particulières de sin et cos Angle 0 π/6
30°π/4
45°π/3
60°π/2
90°sin 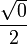
0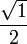
1/2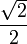
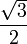
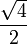
1cos 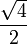
1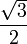
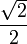
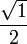
1/2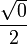
0tan 0 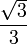
1 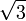
ind. - Autres valeurs remarquables :
Zéros
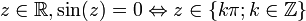 .
.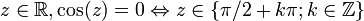 .
.Définitions à partir du cercle unité
Les six fonctions trigonométriques peuvent également être définies à partir du cercle unité. La définition géométrique ne fournit presque pas de moyens pour le calcul pratique; en effet elle se fonde sur des triangles rectangles pour la plupart des angles. Le cercle trigonométrique, en revanche, permet la définition des fonctions trigonométriques pour tous les réels positifs ou négatifs, pas seulement pour des angles de mesure en radians comprise entre
 .
.Dans un plan muni d'un repère orthonormé
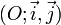 , le cercle trigonométrique est le cercle de centre O et de rayon 1. Si l'on considère un point A(xA, yA) sur le cercle, alors on a :
, le cercle trigonométrique est le cercle de centre O et de rayon 1. Si l'on considère un point A(xA, yA) sur le cercle, alors on a :Sur le cercle ci-contre, nous avons représenté certains angles communs, et nous avons indiqué leurs mesures en radians figurant dans l'intervalle [ − 2π,2π], soit deux mesures par angle et même trois pour l'angle nul.
Notez que nous mesurons les angles positifs dans le sens trigonométrique, contraire à celui des aiguilles d'une horloge, et les angles négatifs dans le sens horaire. Une demi-droite qui fait un angle θ avec la demi-droite positive 0x de l'axe des abscisses coupe le cercle en un point de coordonnées (cosθ,sinθ). Géométriquement, cela provient du fait que l'hypoténuse du triangle rectangle ayant pour sommets les points de coordonnées (0, 0), (cos θ, 0) et (cos θ, sin θ) est égale au rayon du cercle donc à 1. On a donc
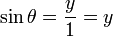 et
et 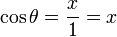 . Le cercle unité peut être considéré comme une façon de regarder un nombre infini de triangles obtenus en changeant les longueurs des côtés opposés et adjacents mais en gardant la longueur de leur hypoténuse égale à 1.
. Le cercle unité peut être considéré comme une façon de regarder un nombre infini de triangles obtenus en changeant les longueurs des côtés opposés et adjacents mais en gardant la longueur de leur hypoténuse égale à 1.Bien que seulement le sinus et le cosinus aient été définis directement par le cercle unité, les autres fonctions trigonométriques peuvent être définies par:
Le cercle unité a pour équation :
Cela donne immédiatement la relation
Relations entre sinus et cosinus
- NB : Les valeurs d'angles sont en radians.
Pour définir les angles strictement plus grands que
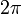 ou strictement négatifs, il suffit d'effectuer des rotations autour du cercle. De cette façon, le sinus et le cosinus deviennent des fonctions périodiques de période
ou strictement négatifs, il suffit d'effectuer des rotations autour du cercle. De cette façon, le sinus et le cosinus deviennent des fonctions périodiques de période 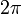 :
:- pour tout angle
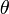 et tout entier k :
et tout entier k : 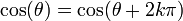
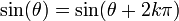
Ceci exprime le caractère périodique de ces fonctions. Grâce au cercle, et avec des considérations géométriques simples, on peut voir que
car
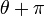 et
et 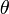 sont diamétralement opposés sur le cercle.
sont diamétralement opposés sur le cercle.car
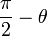 est le point symétrique de
est le point symétrique de 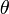 par rapport à la bissectrice de
par rapport à la bissectrice de 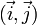 .
.car
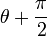 se déduit de
se déduit de 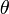 par rotation d'un quart de tour.
par rotation d'un quart de tour.car
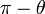 est le symétrique de
est le symétrique de 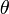 par rapport à
par rapport à 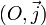 .
.car
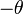 est le symétrique de
est le symétrique de 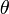 par rapport à
par rapport à 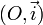 .
.Ces formules font partie des identités trigonométriques.
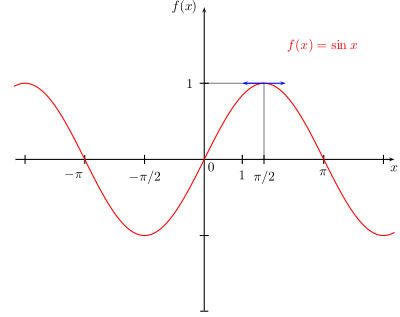
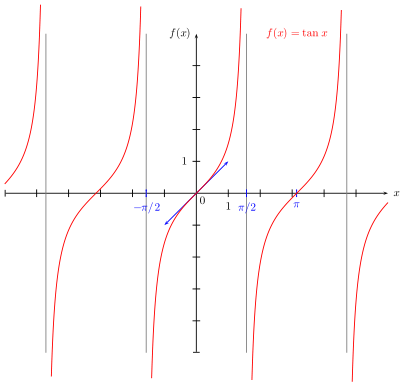
Représentations graphiques
Voici les représentations graphiques des fonctions sinus, cosinus et tangente:
Parité des fonctions
sinus est une fonction impaire :
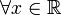 on a
on a 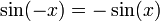
cosinus est une fonction paire :
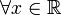 on a
on a 
tangente est une fonction impaire :
 on a
on a 
Limites et dérivées
On a
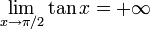 ,
,  ,
, 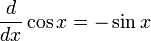 et
et  .
.On trouvera d'autres relations sur la page consacrée aux identités trigonométriques.
Définitions à partir des séries entières
Ici, et généralement en analyse, il est de la plus grande importance que tous les angles soient mesurés en radians. On peut alors définir
Ces définitions sont équivalentes à celles données ci-dessus ; on peut le justifier avec la théorie des séries de Taylor, et avec le fait que la dérivée du sinus est le cosinus et que celle du cosinus est l'opposé du sinus.
Ces définitions sont souvent utilisées comme point de départ des traités rigoureux d'analyse et de la définition du nombre π puisque la théorie des séries est bien connue. La dérivabilité et la continuité sont alors faciles à établir, de même que les formules d'Euler en analyse complexe reliant les fonctions trigonométriques à la fonction exponentielle, ainsi que l'identité d'Euler. Les définitions utilisant les séries ont l'avantage supplémentaire de permettre de prolonger les fonctions sinus et cosinus en des fonctions analytiques dans tout le plan complexe.Il n'est pas possible d'obtenir des séries aussi simples pour les autres fonctions trigonométriques, mais on a, par exemple
où Bn est le n-ème nombre de Bernoulli. Ces expressions se traduisent sous forme de fractions continues, elles ont permis à Lambert de démontrer l'irrationalité du nombre π (cf l'article Fraction continue).
Relations avec la fonction exponentielle et les nombres complexes
On peut montrer à partir de la définition des séries que les fonctions sinus et cosinus sont respectivement la partie imaginaire et la partie réelle de la fonction exponentielle quand son argument est imaginaire pur :
Cette relation a été trouvée par Euler.
où i2 = −1.
Voir à ce sujet l'article Trigonométrie complexe
Fonctions réciproques
Les fonctions trigonométriques ne sont pas bijectives. En les restreignant à certains intervalles, les fonctions trigonométriques réalisent des bijections. Les applications réciproques (arcsin, arccos, arctan, arccosec, arcsec et arccotg) sont habituellement définies par :
- pour tous réels x et y tels que
- -1 ≤ x ≤ 1, -π/2 ≤ y ≤ π/2
- y = arcsin(x) si et seulement si x = sin(y)
- pour tous réels x et y tels que
- -1 ≤ x ≤ 1, 0 ≤ y ≤ π,
- y = arccos(x) si et seulement si x = cos(y)
- pour x réel quelconque et y tel que
- -π/2 < y < π/2,
- y = arctan(x) si et seulement si x = tan(y)
- pour tous réels x et y tels que
- (x ≤ -1 ou x ≥ 1), (-π/2 ≤ y ≤ π/2 et y ≠ 0),
- y = arccosec(x) si et seulement si x = cosec(y)
- pour tous réels x et y tels que
- (x ≤ -1 ou x ≥ 1), (0 ≤ y ≤ π et y ≠ π/2),
- y = arcsec(x) si et seulement si x = sec(y)
- pour tous réels x et y tels que
- x ? 0, (0 < y < π et y? π/2),
- y = arccotg(x) si et seulement si x = cotg(y)
Ces fonctions peuvent s'écrire sous forme d'intégrales indéfinies :
Égalités pratiques :
Propriétés et applications
Article détaillé : Applications de la trigonométrie.Les fonctions trigonométriques, comme leur nom le suggère, ont une importance cruciale en trigonométrie, mais interviennent aussi dans l'étude des fonctions périodiques.
En trigonométrie
En trigonométrie, elles fournissent des relations intéressantes entre les longueurs des côtés et les angles d'un triangle quelconque.
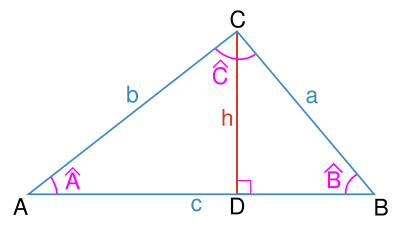
Considérons un triangle quelconque :
- la loi des sinus s'écrit:
Cette relation peut être démontrée en divisant le triangle en deux triangles rectangles et en utilisant la définition ci-dessus du sinus.
Le nombre commun
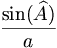 apparaissant dans le théorème est l'inverse du diamètre du cercle circonscrit au triangle (cercle passant par les trois points A, B et C). La loi des sinus est utile pour calculer des longueurs inconnues des côtés dans un triangle quelconque si deux angles et un côté sont connus. C'est une situation courante survenant dans la triangulation, une technique pour déterminer des distances inconnues en mesurant deux angles et une distance.
apparaissant dans le théorème est l'inverse du diamètre du cercle circonscrit au triangle (cercle passant par les trois points A, B et C). La loi des sinus est utile pour calculer des longueurs inconnues des côtés dans un triangle quelconque si deux angles et un côté sont connus. C'est une situation courante survenant dans la triangulation, une technique pour déterminer des distances inconnues en mesurant deux angles et une distance.- la loi des cosinus ou théorème d'Al-Kashi est une généralisation du théorème de Pythagore
À nouveau, ce théorème peut être démontré en divisant le triangle en deux triangles rectangles. La loi des cosinus est utile pour déterminer les données inconnues d'un triangle si deux des côtés et un angle sont connus. Remarquons que l'angle connu doit être contenu dans les deux côtés dont nous connaissons la longueur.
- Il y a également la loi des tangentes :
L'utilisation des fonctions trigonométriques ne se limite pas seulement à l'étude des triangles. Les fonctions trigonométriques sont des fonctions périodiques dont les représentations graphiques correspondent à des modèles caractéristiques d'ondes, utilisés pour modéliser des phénomènes oscillatoires tels que le bruit ou les ondes de la lumière. Chaque signal peut être écrit comme une somme (en général infinie) de fonctions de sinus et de cosinus de différentes fréquences; ce sont les séries de Fourier.
Pour avoir un formulaire de relations entre les fonctions trigonométriques, consultez les identités trigonométriques.
En analyse harmonique
 Animation montrant la décomposition additive d'une onde carrée lorsque le nombre d'harmoniques s'accroît
Animation montrant la décomposition additive d'une onde carrée lorsque le nombre d'harmoniques s'accroît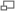
Les fonctions sinus et cosinus apparaissent aussi dans la description d'un mouvement harmonique simple, un concept important en physique. Dans ce contexte les fonctions sinus et cosinus sont utilisées pour décrire les projections sur un espace à une dimension d'un mouvement circulaire uniforme, le mouvement d'une masse au bout d'un ressort, ou une approximation des oscillations de faible écart angulaire d'un pendule.
Les fonctions trigonométriques sont aussi importantes dans d'autres domaines que celui de l'étude des triangles. Elles sont périodiques et leurs représentations graphiques sont des sinusoïdes et peuvent servir à modéliser des phénomènes périodiques comme le son, les ondes de lumière. Tout signal, vérifiant certaines propriétés, peut être décrit par une somme (généralement infinie) de fonctions sinus et cosinus de différentes fréquences ; c'est l'idée de base de l'analyse de Fourier, dans laquelle les séries trigonométriques sont utilisées pour résoudre de nombreux problèmes aux valeurs limites dans des équations aux dérivées partielles. Par exemple une onde carrée, peut être décrite par une série de Fourier :
Histoire
Article détaillé : Histoire des fonctions trigonométriques.Les traces les plus anciennes d'utilisation de sinus seraient apparues dans le Sulba Sutras écrit en indien ancien dans la période du VIIIe siècle av. J.-C. au VIe siècle av. J.-C.
Les fonctions trigonométriques furent plus tard étudiées par Hipparque de Nicée (185-125 av. J.-C.), Âryabhata (476-550), Varahamihira, Brahmagupta, Muhammad ibn Mūsā al-Khuwārizmī, Abu l-Wafa, Omar Khayyam, Bhāskara II, Nasir ad-Din at-Tusi, Regiomontanus (1464), Al-Kachi (quatorzième siècle), Ulugh Beg (quatorzième siècle), Madhava (1400), Rheticus et son disciple Valentin Otho.
L'ouvrage Introductio in analysin infinitorum (1748) de Leonhard Euler fut en grande partie à l'origine des considérations analytiques des fonctions trigonométriques en Europe en les définissant à partir de développements en séries, et présenta les formules d'Euler.
Références
Bibliographie
- Guilmin, Adrien Cours élémentaire de trigonométrie rectiligne Gallica
- Lefébure de Fourcy et Louis-Étienne Eléments de trigonométrie Gallica
- Maor, Eli, Trigonometric Delights, Princeton Univ. Press. (1998). Reprint edition (25 février, 2002): ISBN 0-691-09541-8. (en)
- Needham, Tristan, Preface" to Visual Complex Analysis. Oxford University Press, (1999). ISBN 0-19-853446-9. (en)
- O'Connor, J.J., and E.F. Robertson, Trigonometric functions, Archive de l'histoire des mathématiques de MacTutor. (1996). (en)
- O'Connor, J.J., and E.F. Robertson, Madhava of Sangamagramma, Archive de l'histoire des mathématiques de MacTutor. (2000). (en)
- Pearce, Ian G., Madhava of Sangamagramma, Archive de l'histoire des mathématiques de MacTutor. (2002). (en)
- Weisstein, Eric W., Tangente de MathWorld, consulté le 21 janvier 2006.
Voir aussi
Liens internes
- Algorithme de calcul CORDIC
- Comment construire des tables trigonométriques
- Les fonctions trigonométriques de Wikipédia
- Similarité cosinus
- Sinus cardinal
- Trigonométrie complexe
- Trigonométrie hyperbolique
Liens externes
- Étymologie du mot « sinus »
- GonioLab: Visualisée des Cercle trigonométrique, fonctions de trigonométriques et hyperboliques (Java Web Start)
- Portail des mathématiques
Catégories : Cercle et sphère | Géométrie du triangle | Fonction remarquable | Trigonométrie | Analyse harmonique
Wikimedia Foundation. 2010.