- Orthodromie
-
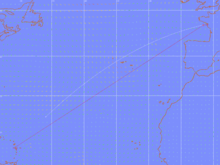 Comparaison entre les routes loxodromique (rouge) et orthodromique (blanc) sur une carte à projection de Mercator
Comparaison entre les routes loxodromique (rouge) et orthodromique (blanc) sur une carte à projection de Mercator
L'orthodromie désigne le chemin le plus court entre deux points d'une sphère, c'est-à-dire l'arc de grand cercle qui passe par ces deux points. Pour les navigateurs, une route orthodromique désigne ainsi la route la plus courte à la surface du globe terrestre entre deux points. Dans la vie courante, cette plus courte distance entre deux points sur Terre est désignée sous le nom de « distance à vol d'oiseau » entre ces deux points.
Sommaire
Représentation sur une carte
Sur une carte en projection de Mercator, l'orthodromie n'est pas représentée par une ligne droite mais par une ligne courbe. En effet, une carte en projection de Mercator conserve les angles mais pas les distances, de sorte que c'est la loxodromie (qui coupe tous les méridiens sous un angle constant) qui y sera représentée par une ligne droite.
Sur une carte en projection gnomonique, l'orthodromie est représentée par une droite. Les cartes en projection gnomonique sont utilisées pour la navigation en latitudes élevées.
Sur une courte distance, on peut confondre orthodromie et loxodromie. La distinction devient importante lors des traversées océaniques pour des parcours E-W (et inversement) et surtout aux latitudes élevées (voir la formule donnant le gain de l'orthodromie sur la loxodromie).
La courbe de l'orthodromie sur la carte Mercator est ouverte vers l'équateur (soit courbée vers le pôle, nord dans l'hémisphère nord, sud dans l'hémisphère sud). Ceci signifie que pour une traversée est-ouest (et inversement) on va se rapprocher du pôle. Le point d'infléchissement de l'orthodromie s'appelle le vertex. La détermination de la latitude du vertex (latitude maximale atteinte) est une grandeur intéressante à déterminer pour préparer une traversée circumpolaire maritime (dans l'hémisphère sud par conséquent, par exemple de Tasmanie au Cap Horn) où il importe de ne pas trop gagner en latitude en raison du danger des glaces et de la banquise. La route choisie alors se décomposera en un tronçon d'orthodromie jusqu'à la latitude extrême que l'on ne veut pas dépasser, puis un tronçon de loxodromie à cette latitude et enfin un autre tronçon d'orthodromie pour remonter jusqu'à destination.
Formule de l'orthodromie
Voici le résultat du calcul de l'orthodromie entre A (φA,λA) et B (φB,λB) avec angles en degrés et distance en milles marins :
- distance orthodromique M :
- gain (m-M) en distance par rapport à la loxodromie :

- avec :
 la distance loxodromique
la distance loxodromique la distance orthodromique
la distance orthodromique la route vraie loxodromique
la route vraie loxodromique la latitude moyenne
la latitude moyenne 
- route initiale
 (angle du tronçon de route initial) :
(angle du tronçon de route initial) :
- latitude du vertex
 :
:
Calcul complet
La détermination numérique directe de la distance à vol d'oiseau entre deux points de la surface terrestre est possible en ligne[1]. Voici le calcul algébrique correspondant.
Question d'unités
Dans la présentation qui suit les angles sont exprimés en radians. Comme les latitudes et les longitudes sont exprimées d'ordinaire en degrés, il faudra faire les conversions nécessaires. Pour passer des degrés au radians :
De même en utilisant sur une calculette les fonctions arccos ou arcsin, il faudra vérifier quelles sont les unités choisies par l'instrument.
Parfois même les longitudes sont données en heures, minutes et secondes. 24 heures correspondent à 360 degrés, donc 1 heure à 15 degrés.
Distance orthodromique entre deux points de la surface terrestre
Calculons la distance à vol d'oiseau entre deux points A et B de la surface terrestre. Sur la sphère le chemin le plus court pour aller du point A au point B consiste à suivre le grand cercle passant par ces points. La plus courte distance de A à B, appelée distance orthodromique, est donc égale à la longueur de l'arc AB sur ce cercle. Un tel chemin représente aussi une géodésique sur la surface. Le principe de calcul de la longueur de cette plus courte route est le suivant. Pour connaître l'arc AB il suffit de déterminer l'angle de sommet O (le centre de la Terre) sous-tendu par le segment AB. On commence par calculer la longueur du segment rectiligne AB (le tunnel en quelque sorte). Puis le sinus de la moitié de l'angle AOB est égal au rapport de AB/2 au rayon de la sphère. On en déduit la valeur de l'angle cherché.
Considérons un repère orthonormé Oxyz. Soient θ et φ les coordonnées angulaires d'un point P sur la sphère (voir la figure), θ étant l'angle entre l'axe Oz et le rayon OP (c'est la colatitude de P : sa latitude est π/2 - θ) et φ l'angle azimutal, c'est-à-dire l'angle polaire que fait la projection de OP sur le plan xOy avec l'axe Ox.
En prenant le rayon de la sphère pour unité, les coordonnées cartésiennes des points A (point 1) et B (point 2) s'expriment en fonction des coordonnées polaires par les formules classiques
et
Le carré de la longueur du segment AB (c'est-à-dire du tunnel virtuel sous Terre) est
soit
La distance rectiligne h = AB/ 2 représente le sinus de la moitié de l'angle au centre AOB recherché. Autrement dit l'arc AB sur la sphère (de rayon pris pour unité, rappelons-le) est
où h est défini par son carré
Pour simplifier cette relation on part de
qui entraîne
soit
En inversant cette dernière formule nous obtenons
et l'expression de l'arc AB devient (toujours sur une sphère de rayon unité)
Sur Terre on repère un point par sa latitude et sa longitude. La latitude lat est le complément à π / 2 de la colatitude θ, ce qui veut dire que
En notant R le rayon terrestre (soit 6 378 kilomètres, rayon équatorial moyen) et en notant long la différence de longitude (ϕ2 - ϕ1) entre les deux points, nous obtenons la formule finale donnant la distance orthodromique entre les points A et B de latitude lat1 et lat2 et de différence de longitude long comme :
Passage aux milles marins
L'usage en navigation est d'utiliser le mille marin comme équivalent de la longueur d'un arc de 1' (une minute d'arc) sur un grand cercle de la surface terrestre et par conséquent sur un méridien (le mille marin international vaut 1 852 mètres).
Il est donc égal, avec les notations précédentes à
où R mesure le rayon moyen de la Terre supposée sphérique. On a donc
ou encore si on exprime l'arc cosinus en degrés
ce qui est la formule donnée initialement.
Notes et références
Voir aussi
Article interne
- Portail du monde maritime
- Portail de l’aéronautique
- Portail de la géométrie
Catégories :- Navigation
- Physique
- Cercle et sphère
Wikimedia Foundation. 2010.

![M = 60\arccos \,[\sin \varphi_A\sin \varphi_B + \cos \varphi_A\cos \varphi_B \cos (\lambda_B - \lambda_A)]\,](9/009a575f4f3c819e8940a9d908c01168.png)







![\mathrm{AB}^2 = 2 \ [1 - \sin\theta_1\sin\theta_2\cos(\varphi_2-\varphi_1) -\cos\theta_1\cos\theta_2 ] \,.](3/223a06c56fc1c7d222c0f048c02296cb.png)

![h^2\,=\, (1/2)\,[1 - \sin\theta_1\sin\theta_2\cos(\varphi_2-\varphi_1) -\cos\theta_1\cos\theta_2 ]\,.](3/313c3cd68ecad32dc63a9f8d83ad8629.png)




![\mathrm{arc(AB)} \,=\, \arccos\ [\sin\theta_1 \sin\theta_2 \cos(\varphi_2-\varphi_1) + \cos\theta_1\cos\theta_2]\,.](d/3cdaef1dcaaac645a49b127f89e7db87.png)

![\mathrm{arc(AB)}\, =\, R \times \arccos\ [\cos(\lambda_1)\cos(\lambda_2)\cos(\varphi) + \sin(\lambda_1)\sin(\lambda_2)] \,.](9/2594e462bb572f9bee292481b4caffe6.png)

![\frac{{\rm arc(AB)}}{{\rm 1\ mille\ marin}}\,=\,\frac{180\times60}{\pi} \arccos\ [\cos(\lambda_1)\cos(\lambda_2)\cos(\varphi) + \sin(\lambda_1)\sin(\lambda_2)]\,,](6/a96bdca533c386882ea4cdddf0dd1523.png)
![\mathrm{arc(AB)}_\mathrm{(milles\ marins)}\,=\,60 \times \arccos{}_\mathrm{(degr\acute es)} [\cos(\lambda_1)\cos(\lambda_2)\cos(\varphi) + \sin(\lambda_1)\sin(\lambda_2)]\, \,](c/56c79c268a43f7cb8b5d70fa6eebe3cd.png)