Arbre De Stern-Brocot

Arbre de Stern-Brocot

En mathématiques, un arbre de Stern-Brocot est une représentation de toutes les fractions irréductibles strictement positives. Cet arbre constitue une manière plutôt élégante de construire l'ensemble des rationnels $\mathbb Q$.

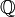Il a été découvert simultanément il y a 150 ans par un mathématicien allemand nommé Moritz Stern, et Achille Brocot, un horloger français.

Construction

Représentation de l'arbre Stern-Brocot

On part du couple de fractions irréductibles (0/1, 1/0), (on affirme que $1/0 = +\infty$).
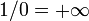Et on répète autant de fois que l'on le souhaite, le procédé suivant :

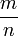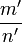Insérer entre $\frac{m}{n}$ et $\frac{m'}{n'}$, la fraction appelée médiante de m/n et m'/n' :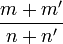 $\frac{m+m'}{n+n'}$

On a tout d'abord donc : 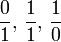$\frac{0}{1},\,\frac{1}{1},\,\frac{1}{0}$ qui constituent les fondements de la construction.

A l'étape suivante on obtient donc : $\frac{0}{1},\,\frac{1}{2},\,\frac{1}{1},\,\frac{2}{1},\,\frac{1}{0}$

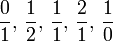
On construit encore quatre fractions ensuite : $\frac{0}{1},\,\frac{1}{3},\,\frac{1}{2},\,\frac{2}{3},\,\frac{1}{1},\,\frac{3}{2},\,\frac{2}{1},\,\frac{3}{1},\,\frac{1}{0}$

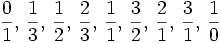
Et ainsi de suite... Mais ainsi défini, on peut imaginer la représentation de cette construction par un arbre binaire que l'on appelle Arbre de Stern-Brocot (voir image).

On remarque au passage que sur l'extrême-gauche se trouvent les fractions unitaires, sur l'extrême-droite, les nombres entiers écrits sous forme rationnelle, le dénominateur étant égal à 1.

Questions

Mais finalement, le procédé étant simple, pourquoi fonctionnerait-il ? Répondons à toutes les questions qui apportera la preuve que la construction est justifiée.

Chaque fraction est-elle irréductible ?

On doit montrer cette relation par récurrence. On pose le fait fondamental :

Si m/n et m'/n' sont deux fractions consécutives sur un même niveau de l'arbre, alors : m'n − mn' = 1

À l'étage 0, c'est évident : on a 1.1 - 0.0 = 1.

Insérons un médiant (m+m')/(n+n'), on doit donc vérifier la relation de récurrence pour ce médiant avec m'/n' et avec m/n.
Il est donc évident de voir que :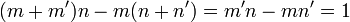

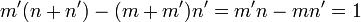
$(m+m')n-m(n+n')= m'n - mn' = 1\,$
$m'(n+n')-(m+m')n'= m'n - mn' = 1\,$

Notre relation est vérifiée et on a l'équation de Bézout de (n+n') et (m+m') avec comme PGCD : 1. Les deux nombres sont donc premiers entre eux.

Une fraction apparait-elle deux fois ?

Non, parce que l'ordre est conservé tout au long de la construction.

Soient les deux fractions m/n et m'/n'. On vérifie donc :

$\frac{m+m'}{n+n'} - \frac{m}{n} = \frac{(m+m')n-m(n+n')}{n(n+n')} = \frac{1}{n(n+n')} > 0$

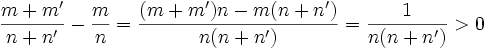
On a encore utilisé la relation fondamentale que l'on a démontrée juste avant. On peut démontrer le même genre de relation avec m'/n'. Et on obtient donc :

$\frac{m}{n} < \frac{m+m'}{n+n'} < \frac{m'}{n'}$

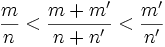
On a gagné !

Tous les éléments de 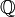$\mathbb Q$ sont-ils dans l'arbre ?

Bien sûr, mais ce n'est pas immédiat ! Prenons a/b tel que a soit premier à b.
On a au départ : 0/1 < a/b < 1/0.
A une étape donnée, on a la configuration : m/n < a/b < m'/n'. En engendrant (m+m')/(n+n'), trois cas s'offrent à nous :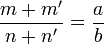

• $\frac{m+m'}{n+n'} = \frac{a}{b}$, et là on arrète le processus (puisqu'on a gagné).
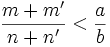• $\frac{m+m'}{n+n'} < \frac{a}{b}$, on pose donc pour l'étape suivante m: = m + m' et n: = n + n'
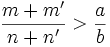• $\frac{m+m'}{n+n'} > \frac{a}{b}$, on pose donc pour l'étape suivante m': = m + m' et n': = n + n'

Or cet algorithme au bout d'un moment s'arrète !

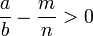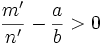On a vu que les conditions : $\frac{a}{b} - \frac{m}{n} > 0$ et $\frac{m'}{n'} - \frac{a}{b} > 0$ entraînent que 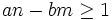$an-bm \geq 1$ et $bm'-an'\geq 1$.

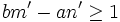Ce qui nous amène à écrire que :
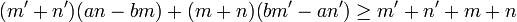$(m'+n')(an-bm)+(m+n)(bm'-an') \geq m'+n'+m+n$ et d'après notre première relation on a : $a+b \geq m'+n'+m+n$.

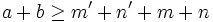Au fur et à mesure des étapes, vous m'accorderez que m' + n' + m + n croit strictement. Donc l'algorithme s'arrêtera (au maximum en a+b étapes d'ailleurs).

Suite de Farey

La suite de Farey d'ordre N, que l'on note F_N, est la suite croissante des fractions réduites comprises entre 0 et 1 dont le dénominateur est inférieur ou égal à N.

L'étroite relation entre Stern-Brocot et cette suite est développé suffisamment dans son article correspondant.

Déplacement dans l'arbre

Idée

Étant donné qu'un rationnel n'apparait qu'une et une seule fois dans l'arbre, alors on peut considérer cet arbre comme un pur système de numération. Prenons la suite des pas que l'on va faire dans l'arbre pour atteindre la fraction souhaité. On définit donc deux "pas" : le pas G (gauche) et le pas D (droite) (dans le livre cité en référence on a L et R mais pour des raisons évidentes de traduction, on mettra G et D). On peut donc représenter tout rationnel positif comme une unique suite de G et D qui représente son chemin dans l'arbre.

Prenons un exemple : considérons le mot GDDG, on part de 1/1 pour arriver à 1/2, puis on va à droite vers 2/3, encore à droite, 3/4, et enfin à gauche 5/7.

On remarque que l'on doit partir de 1/1 (pour avoir un point de départ bien fixé et on suppose que 0 n'est jamais demandé). Convenons pour l'instant de l'appeler "Identité".

Mais comment trouver de façon simple une fraction à partir d'un mot composé de G et de D.

Représentation matricielle

Soit un mot S composé de G et de D, on définit f(S) comme la fraction correspondant à S.

On aimerait trouver un moyen simple pour exprimer f.

Pour cela on va partir d'une représentation matricielle. Si vous ne comprenez pas les calculs ci-dessous, reportez vous à l'article sur les matrices. La théorie pure des matrices n'est pas vraiment utile ici, mais le calcul l'est, cela ne requiert donc aucun niveau d'algèbre linéaire.

On identifiera dans la suite la fraction 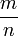$\frac{m}{n}$ à la matrice colonne 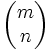$\begin{pmatrix}m \\ n\end{pmatrix}$. Étant donné une telle matrice colonne, on notera 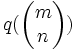$q(\begin{pmatrix}m \\ n \end{pmatrix})$ le rationnel 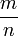$\frac{m}{n}$ associé. Étant donné deux matrices colonnes V₁ et V₂, leur médiant est V₁ + V₂. De façon matricielle, si on définit M comme la matrice 2x2 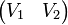$\begin{pmatrix}V_1 & V_2 \end{pmatrix}$ constituée des deux blocs V₁ et V₂, leur médiant est tout simplement $M\begin{pmatrix}1 \\ 1\end{pmatrix}$.

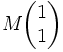Remarquons maintenant que chaque élément V de l'arbre de Stern-Brocot est associé de façon unique aux deux éléments de l'arbre V₁ et V₂ à partir desquels il a été obtenu lors de la construction de l'arbre avec q(V₁) < q(V₂). On note gen(V) la matrice par blocs $\begin{pmatrix} V_2 & V_1\end{pmatrix}$.

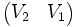Pour calculer f(S), l'idée est alors de calculer récursivement gen(f(S)), qu'on notera $\widehat{S}$

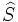
On remarque tout d'abord 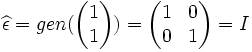$\widehat{\epsilon}= gen(\begin{pmatrix}1 \\ 1\end{pmatrix})= \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix} = I$ (où ε représente le mot vide et I est la matrice identité).

Si 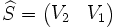$\widehat{S} = \begin{pmatrix}V_2 & V_1\end{pmatrix}$, on a $f(S) = V_1 + V_2 = \begin{pmatrix}V_2 & V_1\end{pmatrix}\begin{pmatrix}1 \\ 1\end{pmatrix}$.

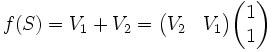D'où :

$\widehat{SD} = \begin{pmatrix}V_2 & f(S)\end{pmatrix} = \widehat{S}\begin{pmatrix} 1 & 1 \\ 0 & 1\end{pmatrix}$

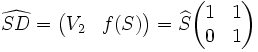
et :

$\widehat{SG} = \begin{pmatrix}f(S) & V_1\end{pmatrix} = \widehat{S}\begin{pmatrix} 1 & 0 \\1 & 1\end{pmatrix}$

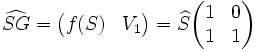
On peut alors définir deux matrices : $\hat{G}=\begin{pmatrix} 1 & 0 \\ 1 & 1\end{pmatrix},\,\hat{D}= \begin{pmatrix} 1 & 1 \\ 0 & 1\end{pmatrix}$.

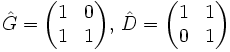Ainsi, on a une façon très agréable de calculer notre fraction puisque si S est le mot 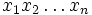$x_1x_2\ldots x_n$, on a 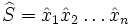$\widehat{S} = \hat{x}_1\hat{x}_2\ldots\hat{x}_n$ et $f(S) = \hat{x}_1\hat{x}_2\ldots\hat{x}_n\begin{pmatrix}1\\ 1\end{pmatrix}$.

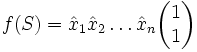Reprenons l'exemple cité précédemment :

$f(GDDG) = \hat{G}\hat{D}\hat{D}\hat{G} = \begin{pmatrix} 1 & 0 \\ 1 & 1\end{pmatrix}\begin{pmatrix} 1 & 1 \\ 0 & 1\end{pmatrix}\begin{pmatrix} 1 & 1 \\ 0 & 1\end{pmatrix}\begin{pmatrix} 1 & 0 \\ 1 & 1\end{pmatrix}\begin{pmatrix}1 \\ 1\end{pmatrix} = \begin{pmatrix} 5 \\ 7\end{pmatrix}$

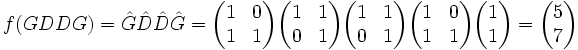
Réciproque / Algorithmes

Comment faire marcher l'algorithme dans l'autre sens ? C’est-à-dire, comment trouver la représentation du chemin effectué pour atteindre une fraction quelconque m/n.

Référence

• Mathématiques concrètes (2nd Edition) de R.L. Graham, D.E. Knuth, O. Patashnik. ISBN 2711748243

Ce document provient de « Arbre de Stern-Brocot ».