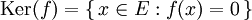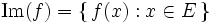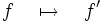Application trilinéaire

Application linéaire

En mathématiques, une application linéaire (aussi appelée opérateur linéaire ou transformation linéaire) est une application entre deux espaces vectoriels qui respecte l’addition des vecteurs et la multiplication scalaire définie dans ces espaces vectoriels, ou, en d’autre termes, qui « préserve les combinaisons linéaires ».

Définitions

Soit ƒ une application de E dans F où E et F sont deux espaces vectoriels sur un corps K.

• L'application ƒ est une application linéaire (ou morphisme de K-espaces vectoriels) si et seulement si :
• $\forall x \in E , \forall y \in E , f(x+y) = f(x) + f(y)$
• $\forall \lambda \in \mathbb K, \forall x \in E, f(\lambda \cdot x) = \lambda \cdot f(x)$

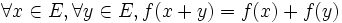
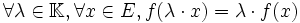
Une application possédant la première propriété est dite additive, et, pour la seconde, homogène.

ƒ est un isomorphisme si ƒ est un morphisme bijectif.

ƒ est un endomorphisme si ƒ est un morphisme ayant même ensemble de départ et d'arrivée.

ƒ est un automorphisme si ƒ est un endomorphisme bijectif.

Si l'ensemble d'arrivée est le corps K on parle de forme linéaire.

On note

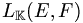• $L_{\mathbb K}(E,F)$ l’ensemble des applications linéaires de E dans F ;
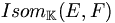• $Isom_{\mathbb K}(E,F)$ l’ensemble des isomorphismes de E dans F;
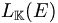• $L_{\mathbb K}(E)$ l’ensemble des endomorphismes de E;
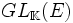• $GL_{\mathbb K}(E)$ (appelé aussi le groupe linéaire) l’ensemble des automorphismes de E.

Comme son nom l'indique, le groupe linéaire, muni de la composition, est un groupe.

Noyau et Image

Si ƒ est une application linéaire de E dans F, on définit le noyau de ƒ, noté Ker(ƒ) (Kern signifie « noyau » en allemand), et l’image de ƒ, notée Im(ƒ), par

$\operatorname{Ker}(f)=\{\,x\in E:f(x)=0\,\}$

$\operatorname{Im}(f)=\{\,f(x):x\in E\,\}$

ker(ƒ) est un sous-espace vectoriel de E et im(ƒ) est un sous-espace de F.

La formule suivante, valable pour un espace E de dimension finie, est souvent utile :

$\dim(\operatorname{Ker}( f )) + \dim(\operatorname{Im}( f )) = \dim( E ) \,$.

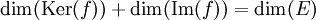Elle est aussi appelée théorème du rang.

Le nombre dim( Im(ƒ) ) est aussi appelé rang de ƒ et est noté rg(ƒ). Si E et F sont de dimension finie et ƒ est représenté par la matrice A, alors le rang de ƒ est égal au rang de la matrice A.

Exemples

• la fonction linéaire « habituelle » : $f : x \mapsto a\cdot x$ où a est un scalaire ;
• les combinaisons linéaires de vecteurs
• l’application dérivation :

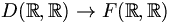
  d : $D(\mathbb{R},\mathbb{R}) \to F(\mathbb{R},\mathbb{R})$

  $f\quad \mapsto\quad f'$

Propriétés

• L'ensemble des applications linéaires de E dans F est un espace vectoriel.

En effet, L(E, F) est un sous-espace vectoriel de l'ensemble des applications de E dans F. Il est non vide car contient l'application nulle. Si a et b sont deux applications linéaires, leur somme est toujours linéaire. On remarque enfin que si λ est un élément de K, l'application λ.a est aussi linéaire.

• Une application linéaire a de L(E, F) est entièrement déterminée par l'image d'une base de E.

En effet, soit (e_i) pour i élément de I une base de E et x un vecteur de E. Alors il existe une famille presque nulle (λ_i) de coefficients tel que :

$x=\sum_{i \in I} \lambda_i\cdot e_i$

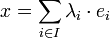
La linéarité de a montre que l'image de x est parfaitement déterminée par la connaissance des images de la base :

$a(x)=a\Big(\sum_{i \in I} \lambda_i\cdot e_i\Big) = \sum_{i \in I} \lambda_i\cdot a(e_i)$

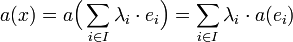
• Si E et F sont de dimension finie alors la dimension de L(E,F) est égale au produit de la dimension de E par la dimension de F.

Pour déterminer la dimension de L(E, F) le plus simple est de déterminer une base de cet espace. Soit (e_i) pour i variant de 1 à n une base de E et (f_j) pour j variant de 1 à m une base de F. Soit a_αβ l'application qui a pour image du vecteur e_i : f_β si i est égal à α et le vecteur nul sinon.

La famille (a_ij) est libre. En effet considérons une combinaison linéaire c non nulle de cette famille :

$c= \sum_{ij}\lambda_{ij}a_{ij}\,$

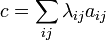
Au moins un coefficient λ_αβ est non nul. Alors c(e_α) est non nul car son coefficient sur pour le vecteur f_β est non nul, ce qui montre que c est non nulle. La seule combinaison linéaire nulle est triviale, ce qui montre que la famille est libre.

La famille (a_ij) est génératrice. Soit b un élément de L(E, F). Notons μ_ij les coordonnées du vecteur e_i dans la base considérée de F. Soit b' l'application linéaire définie par :

$b'=\sum_{ij}\mu_{ij}a_{ij}\,$

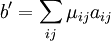
Les applications b et b' sont confondues sur une base de l'ensemble de départ. Elles sont toutes deux linéaires et donc égales. Ainsi, toute applications linéaire de L(E, F) est combinaison linéaire de la famille. Ce qui démontre son caractère générateur.

Le cardinal de cette base est bien le produit de la dimension de E par celle de F, ce qui termine la démonstration. Le calcul de l'image d'un vecteur par une application linéaire à l'aide de l'utilisation d'une base utilise le concept de matrice.

Théorèmes

• Théorème de Banach-Steinhaus
• Théorème de Hahn-Banach

Voir aussi

• Espace vectoriel normé
• Algèbre linéaire
• Équation linéaire
• Système d'équations linéaires
• Spectre d'un opérateur linéaire

Ce document provient de « Application lin%C3%A9aire ».