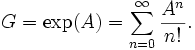- Antisymétrisation
-
Matrice antisymétrique
En mathématiques, et plus précisément en algèbre linéaire, une matrice antisymétrique est un type de matrice carrée.
Sommaire
Définition
Une matrice carrée A à coefficients dans un anneau quelconque est dite antisymétrique si sa transposée est égale à son opposée ; c'est-à-dire si elle satisfait à l'équation :
- tA = -A
c’est-à-dire si elle est écrite avec des coefficients sous la forme A = (ai,j):
- pour tout i et j, ai,j = - aj,i
Exemple
Par exemple, la matrice suivante est antisymétrique:
Le cas où les coefficients de la matrices sont à valeurs dans un corps de caractéristique 2 est très particulier. Dans ce cas, − A = A et donc une matrice est antisymétrique si elle est symétrique. Dans tout ce qui suit, les coefficients de la matrices sont à valeurs dans un corps de caractéristique différente de 2.
Propriétés
- Toutes les entrées de la diagonale principale d'une matrice antisymétrique ont un zéro: en effet il faut que chaque élément de la diagonale vérifie aussi ai,j = - aj,i et le seul nombre ayant cette caractéristique est 0 ; ainsi, la trace d'une matrice antisymétrique est nulle.
- L'espace des matrices symétriques et celui des matrices antisymétriques sont supplémentaires dans l'espace des matrices carrées. En effet, toute matrice carrée se décompose de façon unique de la façon suivante :
-
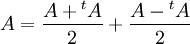 .
.
- Ces espaces sont même orthogonaux si on munit l'espace des matrices carrés du produit scalaire canonique dont une des expressions est justement :
- Les matrices antisymétriques de type (n,n) forment un espace vectoriel de dimension (n2 - n)/2. La base canonique est la famille
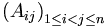 de matrices Aij qui comportent un à la ième ligne et jème colonne et moins un à la jème ligne et ième colonne.
de matrices Aij qui comportent un à la ième ligne et jème colonne et moins un à la jème ligne et ième colonne.
- Dans le cas réel :
Cet espace vectoriel est l'espace tangent au groupe orthogonal O(n). Dans ce sens, nous pouvons assimiler les matrices antisymétriques à des « rotations infinitésimales ».
Toute matrice antisymétrique réelle est diagonalisable sur le corps des complexes et ses valeurs propres sont imaginaires pures. En fait, si A est antisymétrique réelle, iA est matrice hermitienne.
En fait, les matrices antisymétriques de type (n, n) forment une algèbre de Lie utilisant le crochet de Lie
et c'est l'algèbre de Lie associée au groupe de Lie O(n).
Une matrice G est orthogonale et a un déterminant égal à 1, c'est-à-dire est un élément de la composante connexe du groupe orthogonal où se trouve la matrice unité, si et seulement si il existe une matrice antisymétrique A telle que:
Voir aussi
- Portail des mathématiques
Catégorie : Matrice remarquable
Wikimedia Foundation. 2010.

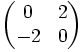
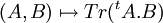
![[A,B] = AB - BA\,](/pictures/frwiki/56/8d8ca025c6fa33a11b2ba7181ff2fc7f.png)