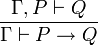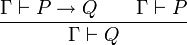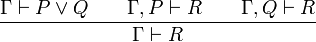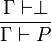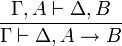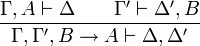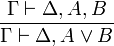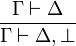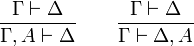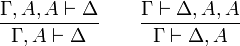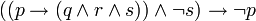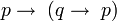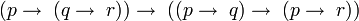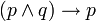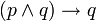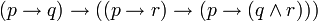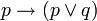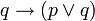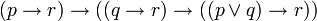- Antilogie
-
Calcul des propositions
 Pour les articles homonymes, voir Déduction.
Pour les articles homonymes, voir Déduction.Le calcul des propositions ou calcul propositionnel est une théorie logique qui définit les lois formelles du raisonnement. C'est la version moderne de la logique stoïcienne. C'est aussi la première étape dans la construction des outils de la logique mathématique.
Sommaire
Introduction générale
Assez complexe à définir en général, la notion de proposition a fait l'objet de nombreux débats au cours de l'histoire de la logique ; l'idée consensuelle est qu'une proposition est une construction syntaxique pour laquelle il fait sens de parler de vérité.
En logique mathématique, le calcul des propositions est la première étape dans la définition de la logique et du raisonnement. Il définit les règles de déduction qui relient les propositions entre elles, sans en examiner le contenu ; il est ainsi une première étape dans la construction du calcul des prédicats, qui lui s'intéresse au contenu des propositions et qui est une formalisation achevée du raisonnement mathématique.
Si l'on se place dans la logique classique, le calcul de propositions est une structure algébrique que l'on appelle algèbre de Boole.
Définition d'une proposition
Quoique le calcul des propositions ne se préoccupe pas du contenu des propositions, mais seulement de leurs relations, il peut être intéressant de discuter ce que pourrait être ce contenu.
Une proposition donne une information sur un état de chose. Ainsi « 2 + 2 = 4 » ou « le livre est ouvert » sont deux propositions. En logique classique, une proposition peut prendre uniquement les valeurs vrai ou faux.
Une phrase optative (qui exprime un souhait comme par exemple « Que Dieu nous protège !», une phrase impérative (« viens !», « tais-toi !») ou une interrogation n'est pas une proposition. « Que Dieu nous protège !» ne pouvant être ni vraie ni fausse: elle exprime uniquement un souhait du locuteur. En revanche, une phrase comme « Dans ce calcul, toutes les variables informatiques sont strictement positives » est une proposition dont le contenu a été modifié par le quantificateur toutes. Ce type de proposition est étudié dans la logique modale, plus précisément la logique temporelle dans ce cas.
Définition d'un système déductif
Un calcul ou un système déductif est, en logique, un ensemble de règles permettant en un nombre fini d'étapes et selon des règles explicites de déterminer si une proposition est vraie. Un tel procédé s'appelle une démonstration.
On associe aussi aux propositions une structure mathématique qui permet de garantir que ces raisonnements ou démonstrations ont du sens, on dit qu'on lui a donné une sémantique. En calcul des propositions classique, cette sémantique est constituée des deux éléments vrai et faux (souvent notés 1 et 0).
Quand on donne du sens à une proposition on lui donne soit la valeur vrai on dit alors qu'il s'agit d'une tautologie, soit la valeur faux, on dit alors qu'il s'agit d'une antilogie.
Structure
Dans les théories de la logique mathématique, on considère donc deux points de vue dits syntaxique et sémantique, c'est le cas en calcul des propositions.
- Aspect syntaxique : il s’agit de définir le langage du calcul des propositions par les règles d’écriture des propositions.
- Aspect sémantique : il s’agit ici de donner un sens aux symboles représentant les connecteurs logiques en fonction de la valeur de vérité des propositions de base (ainsi
 signifie non). Ce sens est donné, par exemple, par des tables de vérité ou par des modèles de Kripke. Puis de décrire les règles d’inférence permettant la déduction de propositions à partir d'autres. Ces règles de déduction permettent d'engendrer des propositions spécifiques que l'on appelle des théorèmes.
signifie non). Ce sens est donné, par exemple, par des tables de vérité ou par des modèles de Kripke. Puis de décrire les règles d’inférence permettant la déduction de propositions à partir d'autres. Ces règles de déduction permettent d'engendrer des propositions spécifiques que l'on appelle des théorèmes.
Le fait que la déduction corresponde parfaitement à la sémantique s'appelle la complétude.
Le système exposé ci-dessous se situe dans le cadre de la logique classique, qui est la branche de la logique mathématique la plus utilisée en mathématiques. On trouvera plus loin une présentation de logiques non classiques. L'adjectif « classique » ne doit pas être pris dans un sens de « normalité », mais comme un attribut que lui a donné l'histoire de la logique, elle aurait tout aussi bien pu s'appeler « booléenne ».
Présentation
Syntaxe
Les constituants du langage
A la base de la syntaxe du calcul des propositions sont les variables propositionnelles ou propositions atomiques, notées p, q, etc., formant un ensemble infini dénombrable.
Les deuxièmes constituants de base du langage du calcul des propositions sont les opérateurs ou connecteurs. Ce sont des symboles qui permettent de construire des propositions plus élaborées. Les plus courants de ces connecteurs logiques sont et ∧, ou ∨, non ¬, implique →, équivaut ↔. On considère souvent aussi la constante ⊥ qui vise à représenter le faux.
À côté de ces symboles on utilise des parenthèses pour lever les ambiguïtés dans les formules. Il existe cependant des systèmes où elles ne sont pas nécessaires, comme dans la notation polonaise, inventée par le logicien polonais Jan Łukasiewicz. Cependant à la suite, entre autres, de Christopher Strachey, les logiciens accordent de moins en moins d'attention à la syntaxe concrète choisie pour se consacrer au fond des choses[1]: la déduction et la sémantique. Ils utilisent ainsi des conventions comme l'associativité pour lever des ambiguïtés et économiser des parenthèses.
Un ensemble de connecteurs propositionnels est dit complet [2]si tout connecteur peut se définir au moyen des connecteurs de l'ensemble. Ainsi l'ensemble {¬, →} est complet : la disjonction se définit par: A∨B = (¬A)→B.
L'ensemble constitué du seul connecteur NON-ET (noté « | » par Henry Sheffer) est également complet, ¬P étant équivalent à P|P et P∨Q à (P|P) | (Q|Q). Cette particularité est utilisée pour la construction de circuits logiques, une seule porte suffisant alors pour concevoir tous les circuits existants.
Les formules bien formées ou propositions
Le calcul des propositions repose de plus sur des règles de formation indiquant comment construire des propositions complexes syntaxiques bien construites ou « bien formées ».
Une proposition ou formule bien formée (notée par la suite A, B, C ou P, Q, R est définie par induction sur la structure des expressions[3] comme suit :
- une variable propositionnelle p est une proposition[4],
- 0 (ou ⊥) et 1 sont des propositions.
- si P et Q sont des propositions, alors (P ∧ Q), (P ∨ Q), (P → Q), (P ↔ Q) et ¬P sont des propositions.
Exemples : Si P, Q et R sont des propositions,
-
- (P → Q) → (¬Q → ¬P) est une proposition.
- (P → ⊥) → ⊥ est une proposition.
- P ∧ ¬P est une proposition.
- (P ∧ Q) ∨ R est une proposition.
- P ∧ Q ∨ n'est pas une proposition.
Quelques conventions syntaxiques
Afin d'alléger la présentation des expressions sans mettre en péril l'absence d'ambiguïté, on autorise par des conventions syntaxiques certaines entorses à la définition ci-dessus.
- On omet généralement les parenthèses extrêmes des formules.
- On supprime les parenthèses en associant les expressions de droite à gauche quand il s'agit du même connecteur.
On démontre que seules les parenthèses ouvrantes sont nécessaires à la non-ambiguïté de la lecture des formules qui pour cette raison sont remplacées par un point "." dans certaines notations.
Les systèmes déductifs
Article détaillé : Théorie de la démonstration.Le calcul des proposition permet de présenter les trois systèmes déductifs les plus connus. On se limite pour cela aux propositions contenant, outre les variables propositionnelles, seulement des implications, des disjonctions et des occurrence de faux autrement dit de ⊥. On admet que ¬P est un abréviation de P → ⊥. Si P est un théorème, autrement dit une proposition qui a une démonstration, on note cela par
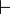 P.
P.Les systèmes déductifs utilisent des règles de déduction (appelées aussi règles d'inférence) qui s'écrivent:
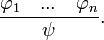
Les
 sont appelées les prémisses et ψ est appelée la conclusion.
sont appelées les prémisses et ψ est appelée la conclusion.La déduction à la Hilbert
Il n'y a qu'une seule règle appelée le modus ponens, elle s'écrit:
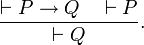
Elle peut se comprendre ainsi si
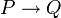 est un théorème et P est un théorème alors Q est un théorème. À cela, on peut ajouter trois axiomes pour l'implication et le faux et trois axiomes pour la disjonction:
est un théorème et P est un théorème alors Q est un théorème. À cela, on peut ajouter trois axiomes pour l'implication et le faux et trois axiomes pour la disjonction:-
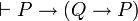 ,
, ,
,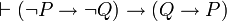 ,
,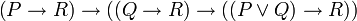 ,
,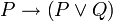 ,
,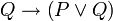 .
.
La déduction naturelle
Alors que la déduction à la Hilbert manipule et démontre des théorèmes, la déduction naturelle démontre des propositions sous des hypothèses et quand il n'y a pas (plus) d'hypothèses, ce sont des théorèmes. Pour dire qu'une proposition P est conséquence d'un ensemble Γ d'hypothèses, on écrit
 . Alors que dans la déduction à la Hilbert, il n'y a qu'une règle et plusieurs axiomes, dans la déduction naturelle il y a un seul axiome et plusieurs règles. Pour chaque connecteur, on classe les règles en règles d'introduction et en règles d'élimination.
. Alors que dans la déduction à la Hilbert, il n'y a qu'une règle et plusieurs axiomes, dans la déduction naturelle il y a un seul axiome et plusieurs règles. Pour chaque connecteur, on classe les règles en règles d'introduction et en règles d'élimination.- L'axiome est
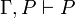 .
. - La règle d'introduction de l'implication:
- La règle d'élimination de l'implication:
- Les deux règles d'introduction de la disjonction, droite et gauche:
- La règle d'élimination de la disjonction:
- La règle d'élimination du faux:
En outre, il faut une règle qui est la réduction à l'absurde, nécessaire en logique classique:
On remarquera que la règle d'élimination de l'implication est très proche du modus ponens, d'ailleurs on l'appelle aussi modus ponens. On remarquera qu'il n'y pas de règle d'introduction du faux et que la règle d'élimination du faux revient à dire que si d'un ensemble d'hypothèses je déduis le faux (ou l'absurde) alors de ce même ensemble je peux déduire n'importe quoi. On remarquera que la réduction à l'absurde est la règle qui correspond au raisonnement par l'absurde: pour démontrer P, on ajoute
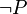 aux hypothèses et si l'on obtient l'absurde, alors on a P.
aux hypothèses et si l'on obtient l'absurde, alors on a P.Le calcul des séquents
L'une des idées qui à conduit au calcul des séquents est de n'avoir plus que des règles d'introduction en plus d'une règle que l'on appelle coupure et de règles structurelles. Pour cela, on utilise des formules que l'on appelle des séquents et qui sont de la forme
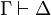 où Γ et Δ sont des multiensembles de propositions. Le séquent
où Γ et Δ sont des multiensembles de propositions. Le séquent 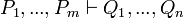 s'interprète comme l'assertion de la conjonction des Pi on déduit la disjonction des Qj. Les Pi sont appelés les antécédents et les Qj sont appelés les conséquents. Si la liste des antécédents est vide on écrit
s'interprète comme l'assertion de la conjonction des Pi on déduit la disjonction des Qj. Les Pi sont appelés les antécédents et les Qj sont appelés les conséquents. Si la liste des antécédents est vide on écrit 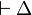 , si la liste des conséquents est vide on écrit
, si la liste des conséquents est vide on écrit 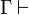 . Un théorème est encore un séquent sans antécédents et avec un seul conséquent.
. Un théorème est encore un séquent sans antécédents et avec un seul conséquent.- L'axiome est
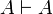 .
.
- Introduction de l'implication à droite :
- Introduction de l'implication à gauche :
- Introduction de la disjonction à droite :
- Introduction de la disjonction à gauche :
- Introduction du faux à droite :
- Introduction du faux à gauche, il a la forme d'un axiome :
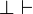
- Coupure :
- Affaiblissements :
- Contractions
Une coupure traduit l'attitude du mathématicien qui démontre un lemme (la proposition A) dont il se sert ailleurs dans la démonstration d'un théorème. Ce lemme peut exprimer quelque chose qui n'a rien à voir avec le théorème principal, d'où le souhait d'éliminer ces lemmes qui sont comme des détours dans la progression vers le résultat principal[5]. Un affaiblissement correspond à l'ajout d'une proposition superflue soit comme antécédent, soit comme conséquent.
Exemples de théorèmes
Nous indiquons ci-dessous une liste de théorèmes qu'on peut démontrer à l'aide des règles précédentes, ainsi que le nom usuel qui leur est attribué par la tradition.
-
-
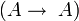
identité 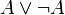
tiers exclu 
double négation 
double négation classique 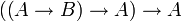
loi de Peirce 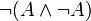
non contradiction 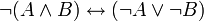
lois de De Morgan 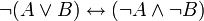
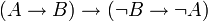
contraposition 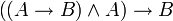
modus ponens (propositionnel) 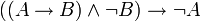
modus tollens (propositionnel) 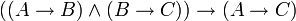
modus barbara (propositionnel) 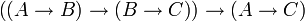
modus barbara (implicatif) 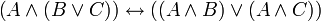
distributivité 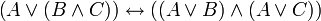
-
Commentaires
On aura remarqué que les trois systèmes utilisent le même symbole
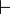 , mais en fait cette notation est cohérente. Le format
, mais en fait cette notation est cohérente. Le format  utilisé pour la déduction naturelle est en fait un séquent dans lequel il n'y a qu'une seule conclusion, on parle alors d'un séquent naturel. Le format
utilisé pour la déduction naturelle est en fait un séquent dans lequel il n'y a qu'une seule conclusion, on parle alors d'un séquent naturel. Le format 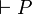 utilisé pour les théorèmes dans les systèmes à la Hilbert correspond à un séquent naturel où il n'y a pas d'hypothèse.
utilisé pour les théorèmes dans les systèmes à la Hilbert correspond à un séquent naturel où il n'y a pas d'hypothèse.On peut montrer que ces trois systèmes sont équivalents dans le sens où ils ont exactement les mêmes théorèmes.
L'aspect « classique » du calcul des propositions est obtenu, dans le système à la Hilbert, par l'axiome de contraposition
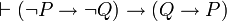 , il apparaît dans la déduction naturelle à travers la réduction à l'absurde. Le calcul des séquents est classique, mais si l'on se restreint aux séquents avec un seul conséquent, il devient intuitionniste.
, il apparaît dans la déduction naturelle à travers la réduction à l'absurde. Le calcul des séquents est classique, mais si l'on se restreint aux séquents avec un seul conséquent, il devient intuitionniste.Sémantique
-
- Ce que j'ai appris de la logique, c'est cette dissociation entre vérité et prouvabilité. Alain Connes, in Triangle de pensées Ed. Odile Jacob, (2000).
Article détaillé : théorie des modèles.La sémantique détermine les règles d'interprétations des propositions. Attribuer des valeurs de vérité[6] à chacune des propositions élémentaires intervenant dans une proposition revient à choisir un modèle de cette proposition.
De façon plus précise, l'interprétation d'une proposition A est le fait d'attribuer une valeur de vérité (0 ou 1) aux variables propositionnelles et à expliquer comment les connecteurs se comportent vis-à-vis des valeurs de vérité. On donne ce comportement par une table de vérité. De cette manière on peut donner un valeur 0 ou 1 à chaque propositions qui dépend des valeurs prises par les tables de vérité. Il existe trois cas d'interprétation:
- Quand la proposition prend toujours la valeur 0 quelles que soient les valeurs des variables propositionnelles, la proposition est dite être une antilogie ou une contradiction. On dit également qu'elle est insatisfaisable.
- Lorsque la proposition A prend toujours la valeur 1, A est une tautologie. On dit aussi que A est valide et on notera cette assertion
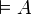 .
. - Si la proposition prend au moins une fois la valeur 1, on dit que l'on peut satisfaire A, ou que A est satisfaisable (ou encore "satisfiable" par mimétisme avec le terme anglais).
- Si la proposition prend au moins une fois la valeur 1 et au moins une fois la valeur 0, c'est une proposition synthétique ou contingente.
Interprétation des connecteurs
Nous explicitons le comportement, puis donnons la table associée
-
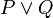 prendra la valeur 1 si et seulement si au moins l'une des deux propositions P ou Q prend la valeur 1.
prendra la valeur 1 si et seulement si au moins l'une des deux propositions P ou Q prend la valeur 1.
-
-
-
-
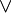
0 1 0 0 1 1 1 1
-
-
-
-
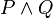 prendra la valeur 1 si et seulement si les deux propositions P et Q prennent simultanément la valeur 1.
prendra la valeur 1 si et seulement si les deux propositions P et Q prennent simultanément la valeur 1.
-
-
-
-
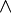
0 1 0 0 0 1 0 1
-
-
-
-
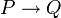 prendra la valeur 0 si et seulement si P prend la valeur 1 et Q la valeur 0.
prendra la valeur 0 si et seulement si P prend la valeur 1 et Q la valeur 0.
-
-
-
-

0 1 0 1 1 1 0 1
-
-
-
-
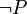 prendra la valeur 1 si et seulement si P prend la valeur 0.
prendra la valeur 1 si et seulement si P prend la valeur 0.
-
-
-
-

0 1 1 0
-
-
-
-
 prendra la valeur 1 si et seulement si P et Q ont la même valeur.
prendra la valeur 1 si et seulement si P et Q ont la même valeur.
-
-
-
-
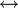
0 1 0 1 0 1 0 1
-
-
-
-
 prend la valeur 0.
prend la valeur 0.
Exemple 1 :
-
- (¬A → A) → A est une tautologie.
En effet, si on attribue à A la valeur 0, alors ¬A prend la valeur 1, (¬A → A) prend la valeur 0, et (¬A → A) → A prend la valeur 1. De même, si on attribue à A la valeur 1, alors ¬A prend la valeur 0, (¬A → A) prend la valeur 1, et (¬A → A) → A prend la valeur 1.
Exemple 2 :
-
- A → (A → ¬A) n'est pas une tautologie.
En effet, si on attribue à A la valeur 1, alors ¬A prend la valeur 0, (A → ¬A) prend la valeur 0, et A → (A → ¬A) prend la valeur 0.
Le calcul propositionnel dispose donc de plusieurs moyens différents pour « valider » les propositions : les systèmes de déduction qui démontrent les théorèmes et les méthodes sémantiques qui définissent[7] les tautologies. La question qui se pose est de savoir si ces méthodes coïncident.
Principales propriétés
Décidabilité, cohérence, complétude, compacité
Le fait que toute proposition soit démontrable si et seulement si elle est une tautologie exprime une propriété du calcul propositionnel que l'on appelle la complétude, cela signifie que la présentation déductive du calcul propositionnel est équivalente à la présentation sémantique. La complétude repose sur les remarques suivantes.
- Toute proposition démontrée résulte d'un axiome ou de l'application d'une règle sur des propositions déjà démontrées. Or il est facile de vérifier que les axiomes fournissent des tautologies et que les règles conservent les tautologies. Toute proposition démontrée est donc une tautologie. Le calcul propositionnel est correct.
- La réciproque repose sur le fait suivant: on peut démontrer que pour toute proposition P du calcul propositionnel il existe une proposition P' telle que
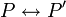 et telle que P' soit sous une forme dite normale
et telle que P' soit sous une forme dite normale 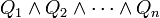 où chaque Qi est de la forme
où chaque Qi est de la forme 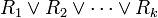 , où chaque Ri est un littéral (c'est-à-dire une proposition de la forme p ou
, où chaque Ri est un littéral (c'est-à-dire une proposition de la forme p ou 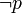 ). Si P' est une tautologie, alors dans chaque Qi, apparaissent nécessairement une variable propositionnelle p et sa négation
). Si P' est une tautologie, alors dans chaque Qi, apparaissent nécessairement une variable propositionnelle p et sa négation 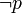 . Sinon il existerait Qi qui ne vérifierait pas cette condition et il serait possible d'attribuer des valeurs aux pj de façon à donner la valeur 0 à Qi, et donc à P' lui-même. Mais on peut montrer que
. Sinon il existerait Qi qui ne vérifierait pas cette condition et il serait possible d'attribuer des valeurs aux pj de façon à donner la valeur 0 à Qi, et donc à P' lui-même. Mais on peut montrer que  est démontrable (
est démontrable (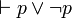 ), puis qu'il en est de même de chaque Qi, puis de P' lui-même et enfin de P. Toute tautologie est alors démontrable. Le calcul propositionnel est complet.
), puis qu'il en est de même de chaque Qi, puis de P' lui-même et enfin de P. Toute tautologie est alors démontrable. Le calcul propositionnel est complet.
L'article théorème de complétude du calcul des propositions propose une autre démonstration plus détaillée.
Il résulte de la complétude du calcul des propositions que :
- Le calcul des propositions est décidable, dans le sens où il existe un algorithme permettant de décider si une proposition est un théorème ou non. Il suffit de dresser sa table de vérité et de voir s'il s'agit d'une tautologie.
- Le calcul des propositions est cohérent (consistant), c'est-à-dire non contradictoire. Il n'existe aucune proposition P telle qu'on puisse avoir en même temps
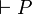 et
et 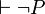 car ces deux propositions seraient des tautologies et on aurait 1 = 0.
car ces deux propositions seraient des tautologies et on aurait 1 = 0. - Le calcul des propositions est fortement complet (maximalement cohérent), dans le sens où tout ajout d'un nouveau schéma d'axiome, non démontrable dans le système initial, rend ce système incohérent.
Supposons donné un nombre infini de propositions. Peut-on satisfaire simultanément ces propositions ? Autrement dit, existe-il des valeurs de vérité pour leurs variables propositionnelles qui donnent 1 comme valeur de vérité à toutes les propositions? Si la réponse est positive pour tout sous-ensemble fini de ces propositions, alors elle l'est pour toutes les propositions. Cette propriété, qui assure que l'on peut passer de tous les sous-ensembles finis à l'ensemble infini tout entier, est appelée la compacité.
Méthodes de calcul, NP-complétude
Nous avons vu que, pour décider si une proposition est démontrable, il suffit de vérifier si c'est une tautologie, c'est-à-dire de vérifier si elle prend la valeur de vérité 1 quelles que soient les valeurs de vérité de ses variables propositionnelles.
Cette approche brutale se heurte cependant au temps de calcul qu'elle requiert. En effet, si la proposition possède n variables propositionnelles, il faut calculer 2n combinaisons de valeurs possibles pour les variables propositionnelles, ce qui devient rapidement infaisable pour n grand. Ainsi, si n = 30, il faudra énumérer plus d'un milliard de combinaisons de valeurs.
Il existe certes des améliorations possibles. Par exemple, si on attribue la valeur de vérité 0 à une variable propositionnelle p, on peut attribuer directement la valeur 0 à
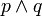 indépendamment de la valeur ultérieure attribuée à q, ce qui diminue le nombre de calculs à effectuer.
indépendamment de la valeur ultérieure attribuée à q, ce qui diminue le nombre de calculs à effectuer.On peut également chercher à voir s'il est possible d'invalider les implications. Considérons par exemple la proposition :
Étant constituée d'une implication, pour la rendre invalide, il suffit que la conclusion
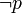 puisse prendre la valeur 0 (et donc p la valeur 1) et que l'hypothèse
puisse prendre la valeur 0 (et donc p la valeur 1) et que l'hypothèse 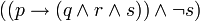 puisse prendre la valeur 1 (et donc
puisse prendre la valeur 1 (et donc  et
et 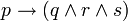 la valeur 1). Mais alors s prend la valeur 0 et
la valeur 1). Mais alors s prend la valeur 0 et 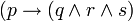 ne peut plus prendre que la valeur 0. Il est donc impossible d'invalider l'implication et celle-ci est une tautologie.
ne peut plus prendre que la valeur 0. Il est donc impossible d'invalider l'implication et celle-ci est une tautologie.Mais les améliorations précédentes ne changent pas fondamentalement la difficulté du problème. On est donc devant la situation suivante. Étant donnée une proposition f, on se demande si f est une tautologie ou non et pour cela, on se demande s'il existe des valeurs de vérité attribuables aux variables propositionnelles de f qui rendraient f invalide.
- Une recherche exhaustive demande 2n vérifications si f possède n variables propositionnelles. Cette démarche est dite déterministe, mais son temps de calcul est exponentiel.
- Par contre, si f n'est pas une tautologie, il suffit d'une vérification à faire, à savoir tester précisément la configuration qui invalide f. Cette vérification demande un simple calcul booléen, qui se fait en temps polynomial (essentiellement linéaire en fait). Le temps de calcul cesse donc d'être exponentiel, à condition de savoir quelle configuration tester. Celle-ci pourrait par exemple être donnée par un oracle ou un être omniscient. Une telle démarche est dite non déterministe.
La question de l'invalidité de f, ainsi que tous les problèmes qui se résolvent suivant la méthode que nous venons d'esquisser, sont dits NP (pour polynomial non déterministe). Tester l'invalidité de f équivaut par des calculs très simples (en temps polynomial) à tester la satisfaisabilité de sa négation. Le problème de la satisfaisabilité d'une proposition, à savoir trouver une configuration qui donne 1 comme valeur de vérité de la proposition est appelé problème SAT. Il joue un rôle fondamental en théorie de la complexité, puisqu'on peut montrer que la découverte d'un algorithme déterministe en temps polynomial pour ce problème permettrait d'en déduire des algorithmes déterministes en temps polynomial pour tous les problèmes de type NP (théorème de Cook). On dit que SAT (et donc également le problème de la non-démontrabilité d'une proposition) est un problème NP-complet. Le problème de la démontrabilité d'une proposition est dit co-NP (pour complémentaire de NP).
Le problème SAT désigne en fait le plus souvent celui de la satisfaisabilité d'une conjonction de clauses (un cas particulier parmi les propositions), mais on ramène le problème de la satisfaisabilité d'une proposition à celui-ci par une réduction polynomiale (une mise sous forme clausale par équisatisfaisabilité, celles par équivalence logique ne fonctionnent pas).
Algèbre de Boole
Soit E l'ensemble des propositions sur un ensemble de variables propositionnelles. Soit
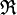 la relation binaire définie sur E par l'équivalence (
la relation binaire définie sur E par l'équivalence (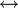 ) entre deux propositions.
) entre deux propositions. 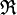 est une relation d'équivalence sur E, compatible avec
est une relation d'équivalence sur E, compatible avec  et
et 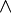 qui donne à l'ensemble quotient E/
qui donne à l'ensemble quotient E/ une structure d'algèbre de Boole.
une structure d'algèbre de Boole.Les algèbres de Boole peuvent être formalisées avec un seul axiome :
-
- (P | (Q | R)) | ((T | (T | T)) | ((S | Q) | ((P | S) | (P | S))))
autrement dit, il suffit de dire que cette proposition vaut 1 pour que toutes les autres identités des algèbres de Boole en découlent.
Veroff et McCune ont démontré en 2000 en utilisant leur système de démonstration automatique de théorèmes Otter que l'on peut formaliser les algèbres de Boole par la seule équation
-
- ((P | R) | Q) | ((P | (P | Q)) | P) = Q.
Formes normales conjonctives, formes normales disjonctives
Articles détaillés : Forme normale disjonctive et Forme normale conjonctive.Une disjonction est une proposition de la forme
 et une conjonction est une proposition de la forme
et une conjonction est une proposition de la forme 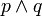 . Une proposition est en forme normale conjonctive (FNC) si elle est composée de conjonctions de disjonctions. Une proposition est en forme normale disjonctive (FND) si elle est composée de disjonctions de conjonctions.
. Une proposition est en forme normale conjonctive (FNC) si elle est composée de conjonctions de disjonctions. Une proposition est en forme normale disjonctive (FND) si elle est composée de disjonctions de conjonctions.Exemples :
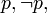
 et
et 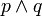 sont à la fois des FNC et des FND.
sont à la fois des FNC et des FND.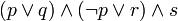 est en forme normale conjonctive.
est en forme normale conjonctive.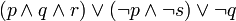 est en forme normale disjonctive.
est en forme normale disjonctive.
Lorsque chaque bloc disjonctif d'une FND comporte une et une seule occurrence des mêmes variables propositionnelles, on parle alors de FND distinguée.
Lorsque chaque bloc conjonctif d'une FNC comporte une et une seule occurrence des mêmes variables propositionnelles, on parle alors de FNC distinguée.
Exemples :
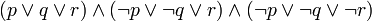 est en forme normale conjonctive distinguée.
est en forme normale conjonctive distinguée.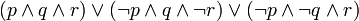 est en forme normale disjonctive distinguée.
est en forme normale disjonctive distinguée.
On peut montrer que toute proposition est équivalente à une FND (en admettant que
 est la disjonction d'un ensemble vide de propositions) et est équivalente à une FNC (en admettant que T est la conjonction d'un ensemble vide de propositions). Autrement dit, pour toute proposition p il existe une proposition q en forme normale disjonctive telle que p
est la disjonction d'un ensemble vide de propositions) et est équivalente à une FNC (en admettant que T est la conjonction d'un ensemble vide de propositions). Autrement dit, pour toute proposition p il existe une proposition q en forme normale disjonctive telle que p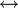 q et une proposition r en forme normale conjonctive telle que p
q et une proposition r en forme normale conjonctive telle que p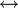 r.
r.Logique classique, minimale, intuitionniste
Les axiomes et règles du calcul propositionnel que nous avons présentés sont ceux de la logique classique. Ils induisent la proposition p ∨ ¬p, appelée principe du tiers exclu, la proposition ¬¬ p → p, appelée élimination de la double négation et la proposition ((p → q) → p) → p appelée loi de Peirce. Cette logique repose sur le principe qu'une propriété P est nécessairement vraie ou fausse. Il est l'un des piliers de la position qualifiée de formaliste, adoptée par Hilbert et d'autres. Or cette position qui implique qu'il y a des démonstrations qui ne construisent pas l'objet satisfaisant la proposition prouvée a été remise en cause par plusieurs mathématiciens, dont le plus connu est Brouwer conduisant à créer par la suite la logique intuitionniste.
Nous présentons maintenant deux variantes très proches de logique non classique, la logique minimale de I. Johansson[8] (1936) et la logique intuitionniste de Heyting (1930). Les connecteurs primitifs sont →, ∧, ∨ et ¬. On garde les deux premiers axiomes de la logique classique :
Avant d'introduire la négation, on énonce les axiomes relatifs à
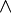 :
:et ceux relatifs à
 , (duaux des précédents) :
, (duaux des précédents) :On introduit enfin deux axiomes relatifs à la négation. Le premier exprime que, si f implique sa propre négation, alors f est invalide.
-
- (p → ¬p) → ¬p.
Le second définit le comportement de chaque logique vis-à-vis d'une contradiction et la seule différence entre la logique minimale et la logique intuitionniste porte sur cet axiome.
-
- ¬p → (p → ¬q) pour la logique minimale et ¬p → (p → q) pour la logique intuitionniste.
En présence d'une proposition et de sa négation, les trois logiques, classique, intuitionniste et minimale, concluent toutes trois à une contradiction ⊥. Mais la différence porte sur l'utilisation que l'on fait de cette contradiction :
- La logique classique déduit de ¬P → ⊥ le fait que P est vrai (raisonnement par l'absurde).
- La logique intuitionniste déduit d'une contradiction que toute proposition est démontrable. De ¬P → ⊥, elle déduit la validité de ¬¬P, propriété plus faible que P.
- La logique minimale déduit d'une contradiction que toute négation de proposition est démontrable, ce qui est plus faible que ce que propose la logique intuitionniste.
Logique minimale et logique intuitionniste ont toutes deux la proposition ¬(p ∧ ¬p) comme théorème. En revanche, p ∨ ¬p n'est pas un théorème de ces logiques.
De même, elles permettent de démontrer p → ¬¬p mais pas la réciproque. Par contre, elles permettent de démontrer l'équivalence entre ¬p et ¬¬¬p. Enfin, la proposition (¬p ∨ q) → (p →q) est un théorème de la logique intuitionniste, mais pas un théorème de la logique minimale.
Glivenko a démontré[9] en 1929 que p est un théorème du calcul propositionnel classique si et seulement si ¬¬p est un théorème du calcul propositionnel intuitionniste. Ce résultat ne s'étend pas si l'on remplace « intuitionniste » par « minimal ». Il ne s'applique pas directement au calcul des prédicats non plus; un codage est toutefois possible, mais c'est plus compliqué.
Notes et références
- ↑ Dans les outils logiciels qui mécanisent la logique sur ordinateur, des outils très développés permettent des syntaxes souples et non ambiguës, associés à d'autres outils qui permettent de modifier la syntaxe pour l'adapter aux goûts de l'utilisateur.
- ↑ Cela ne doit pas être confondu avec la complétude du système déductif par rapport à une sémantique.
- ↑ On parle parfois de clause de clôture qui signifie que l'ensemble des propositions est le plus petit ensemble satisfaisant les trois règles ci-dessus.
- ↑ Par la suite, les variables propositionnelles seront notées p,q,r,s.
- ↑ mais qui peuvent néanmoins la raccourcir considérablement !
- ↑ Les tables de vérités ont été développées originellement par Wittgenstein.
- ↑ Outre la méthode des tables de vérités, il existe une approche sémantique fondée sur les modèles de Kripke.
- ↑ I Johansson, Ingebrigt Der Minimalkalkül, ein reduzierter intuitionistischer Formalismus. Compositio Mathematica, 4 (1937), p. 119-136.
- ↑ Gödel a aussi proposé un codage de la logique classique dans la logique intuitionniste.
Voir aussi
- Gottfried Leibniz - George Boole - Auguste De Morgan - Gottlob Frege - Bertrand Russell - Ludwig Wittgenstein
- Calcul des prédicats
- Déduction naturelle
- Logique mathématique
- Logique intuitionniste
- Sémantique de Kripke, qui est une présentation des modèles de Kripke
- Logique modale
- Logique polyvalente
- Fonction logique
- Porte logique
- Forme normale disjonctive
- Littéral (logique)
Bibliographie
- Quine, Elementary Logic, Harvard University Press - 1980 (1941).
- Robert Blanché, Introduction à la logique contemporaine, Armand Colin - 1951
- A. Heyting, Les Fondements des mathématiques. Intuitionnisme. Théorie de la connaissance, Paris, Gauthiers-Villars, 1955.
- Logique et Connaissance scientifique, Collection de la Pléiade, Gallimard, 1967
- Stephen Kleene, logique mathématique, Armand Colin, 1971 ou Gabay 1987, (ISBN 2-87647-005-5)
- Yannis Delmas-Rigoutsos et René Lalement, La Logique ou l'art de raisonner, 2000 [détail des éditions]
- R. David, K. Nour et C. Raffalli, Introduction à la logique. Théorie de la démonstration. Cours et exercices corrigés, Dunod, 2001, (ISBN 2-10006-796-6)
- G. Dowek, La logique, Coll. Dominos, Flammarion (1995).
- Portail des mathématiques
- Portail de la logique
Catégories : Logique mathématique | Algorithmique | Logique
Wikimedia Foundation. 2010.