Anneau noetherien

Anneau noethérien

Emmy Noether formalise les propriétés d'une famille particulière d'anneaux maintenant appelé anneau noethérien.

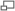
En mathématique, un anneau noethérien est un cas particulier d'anneau, c'est-à-dire d'un ensemble munis d'une addition et d'une multiplication compatible avec l'addition, au sens de la distributivité.

De nombreuses questions mathématiques s'expriment dans un contexte d'anneau, les endomorphismes d'un espace vectoriel ou d'un module sur un anneau, les entiers algébriques de la théorie algébrique des nombres, ou encore les surfaces de la géométrie algébrique. Si les anneaux sont nombreux, rares sont ceux disposant des propriétés communes aux exemples les plus simples comme les entiers relatifs ou les polynômes à coefficients dans un corps. La division euclidienne n'existe en général plus, les idéaux outils majeurs de la théorie des anneaux ne sont plus toujours principaux et le théorème fondamental de l'arithmétique ne possède plus d'équivalent.

L'approche, consistant à étudier une question uniquement sous l'angle des propriétés spécifiques d'une structure d'anneau particulière s'est révélée fructueuse. Richard Dedekind l'a utilisé avec succès en arithmétique et David Hilbert en géométrie algébrique. Emmy Noether, choisit un nombre de propriétés vérifiée par l'anneau plus limité et parvient avec succès à démontrer l'existence de nombreuses propriétés.

Le terme d'anneau noethérien apparait en 1954 sous la plume de mathématiciens japonais^[1].

Approche intuitive

Dans certains cas simples, tout les idéaux d'un anneau A sont principaux. Si A est considéré comme un module sur un anneau, les idéaux sont des sous-modules qui admettent tous une famille génératrice limitée à un élément. Cette situation n'est pas générale.

En arithmétique, il est fréquent d'utiliser des anneaux d'entiers algébrique comme par exemple les entiers quadratiques de la forme a + b.i√5 où a et b sont des entiers relatifs et i l'unité imaginaire complexe. Il existe en effet dans cet anneau un idéal, formé des éléments de la forme 2.a + b(1 + i√5), où a et b sont des entiers relatifs qui ne sont pas principaux. Si cet idéal n'est pas principal, c'est-à-dire n'est pas engendré par un unique élément, en revanche il est engendré par un nombre fini d'éléments, ici deux. Dans l'anneau considéré, c'est-à-dire Z[i.√5] (la lettre Z désigne dans tout l'article l'anneau des entiers relatifs) tous les idéaux sont engendrés par un ou deux éléments. Cette configuration est la même pour tout anneau d'entiers algébriques d'une extension finie du corps des nombres rationnels.

Cette configuration se retrouve en théorie des groupes. Si G est un groupe abélien de type fini c'est-à-dire admettant une famille génératrice fini, il est possible de munir le groupe d'une structure de Z module. Tout sous-groupe de G, qui est aussi un sous-module, admet une famille génératrice finie (cf l'article groupe abélien de type fini). La propriété est la même, même si elle s'applique à un module et non plus à un anneau.

Soit M un module sur un anneau A admettant une base, l'ensemble des endomorphismes L(M) de M est une algèbre sur un anneau est aussi un anneau. Comme l'ensemble des endomorphismes est un module de dimension finie, tout idéal de L(M), qui est aussi un sous module possède une famille génératrice finie. On retrouve une configuration analogue pour les représentations d'un groupe fini avec la notion d'algèbre d'un groupe fini. Dans ces exemples, l'anneau n'est ni intègre ni commutatif.

Cette propriété, indiquant que tout idéal d'un anneau A admet une famille génératrice finie si l'idéal est considéré comme un sous A module est fréquente en mathématiques. Elle correspond à la notion formalisée par la définition d'anneau noethérien et est un peu équivalente à l'hypothèse de la dimension finie en algèbre linéaire.

Définitions

Anneau et module

Article détaillé : module sur un anneau.

De même qu'un corps commutatif est un espace vectoriel sur lui-même, il est possible de considérer un anneau A comme un A module. Si l'anneau n'est pas commutatif, il existe deux produits externes différents : soit λ un élément de A vu comme un scalaire et a un élément de A vu comme un vecteur, les deux produits externes associent respectivement à (λ, a) le vecteur λ.a et a.λ.

Une deuxième différence réside dans les sous-espaces vectoriels. Le corps n'en contient que deux, l'espace réduit à l'élément neutre et lui-même. Pour un A module, la notion de sous-module coïncide avec celle d'idéal. Si le premier produit externe est choisi, on parle d'idéal à gauche, sinon d'idéal à droite. Le module A est possède une famille génératrice constitué d'un unique élément, il suffit de prendre un élément inversible quelconque. Dire que l'anneau est principal revient à dire, avec ce formalisme, que tous les sous-modules admettent une famille génératrice composée d'un unique élément. Ce n'est pas toujours le cas. Dans Z[X], l'anneau des polynômes à coefficients dans Z, l'ensemble des polynômes à coefficient constant pair est un idéal, et donc un sous-module il faut au moins deux éléments comme 2 et X pour engendrer ce sous-module.

Le concept noethérien se définit plus simplement sur un module, la définition d'anneau noethérien devient alors un cas particulier, celui où l'anneau est considéré comme un module sur lui-même.

Définitions

La définition sur les modules est la suivante :

• Soit A un anneau, un A module M est dit noethérien si et seulement si tout sous module de M est engendré par une famille finie.

On en déduit l'équivalent pour les anneaux :

• Un anneau A est dit noethérien à gauche si et seulement si tous les idéaux à gauche admettent une famille génératrice finie, au sens où A est considéré comme un A module.

• Un anneau A est dit noethérien à droite si et seulement si tous les idéaux à droite admettent une famille génératrice finie.

• Un anneau A est dit noethérien s'il est noethérien à droite et à gauche.

Dans le cas des anneaux commutatifs, les trois définitions coïncident.

Il existe deux définitions alternatives et équivalentes, elles se traduisent immédiatement pour les anneaux :

• Soit A un anneau et M un A module, les trois propositions suivantes sont équivalentes :

1. Le A module M est noethérien.
2. Toute suite croissante de sous-modules de M est stationnaire.
3. Toute famille non vide de sous-modules admet un élément maximal pour l'inclusion.

Démonstration

Soit A un anneau. Un idéal M à gauche (resp. à droite) est un sous-module de A pour la multiplication externe qui à au vecteur m élément de M et au scalaire a élément de A associe a.m (resp. m.a). Il suffit donc de montrer la propriété l'équivalence pour les modules, elle est alors aussi démontré pour les anneaux noethériens à gauche, à droite et noethériens.

• Supposons que tout sous module est de type fini et montrons que toute suite croissante de sous-modules (M_i) est stationnaire au bout d'un certain rang :

Un module est dit de type fini s'il admet une famille génératrice finie. Notons N l'union de tous les modules M_i. Comme ils sont emboités, N est un sous-module et elle admet une famille génératrice finie (m_j). Le vecteur m_j est élément de N, il existe donc un indice n_j tel que pour tout i plus grand que n_j, M_i contient m_j. Soit n le maximum de la famille finie des indices j, si i est plus grand que n alors M_i contient la famille (m_j) et donc N. Ceci montre qu'à partir du rang n la famille de sous-modules est stationnaire.

• Supposons que toute suite croissante de sous-modules est stationnaire au bout d'un certain rang et montrons que toute famille possède un élément maximal :

On raisonne par contraposée, on suppose donc qu'une famille (F_i) ne possède pas d'élément maximal. On définit une suite (M_n) d'éléments de F_i strictement croissance. Soit i₁ un élément quelconque de la famille (F_i), on définit M₁ comme égal à F_i1. On suppose la suite définit à l'ordre n, M_n n'est pas un élément maximal de la famille, il existe donc un élément contenant strictement M_n. On définit M_n+1 comme étant égal à cet élément. Il existe alors une suite strictement croissante pour l'inclusion. Par contraposée, la proposition est démontrée.

• Supposons que toute famille possède un élément maximal et montrons que M est de type fini :

Considérons l'ensemble F des sous-modules de type fini de F, par hypothèse il admet un élément maximal N. Cet élément est de type fini par construction, et il existe une famille finie (f_i) qui engendre M. Soit m un élément quelconque de M, le sous-module P engendré par la famille des f_i adjointe à m contient M et est de type fini et donc élément de F. Comme N est maximal et que P le contient, N est égal à P. En conséquence N contient le vecteur m. Comme m est un vecteur quelconque de M, N est égal à M, ce qui montre que le module est de type fini.

 

Propriétés

Dans tout le paragraphe N est un anneau noethérien à gauche et M un A module noethérien. Les démonstrations sur les anneaux noethériens peuvent être courtes. La proposition suivante, utilisée dans l'article Anneau de Dedekind est un exemple :

• Tout idéal à gauche de N contient un produit d'idéaux premiers à gauche.^[2]

Les sous-modules d'un module noethérien sont noethériens, une produit fini de modules noethériens sur un même anneau est aussi noethérien, le quotient d'un module noethérien par un sous-module est aussi noethérien. Ces propriétés se démontrent à l'aide de la proposition suivante :

• Soit P un sous-module de M, le module M est noethérien si et seulement si P et M/P le sont aussi.

Si A est un anneau, la question se pose de savoir si Aⁿ est un module noethérien. Si A n'est pas noethérien, la réponse n'a aucune chance d'être positive, sinon elle est résolue par la proposition suivante :

• Soit n un entier positif, le module à gauche Nⁿ est noethérien.^[3]

Démonstrations

• Tout idéal à gauche de N contient un produit d'idéaux premiers à gauche :

En effet, raisonnons par l'absurde. Soit F la famille des idéaux qui ne contiennent aucun produit d'idéaux premiers, que l'on suppose non vide. Elle contient un idéal maximal J dans F. L'idéal J n'est certainement pas premier (il se contient lui-même et donc contiendrait un produit d'idéaux premiers: J et N). Il existe donc a et b deux éléments de N qui ne sont pas élément de J et tel que a.b est élément de J. Les idéaux J + a.N et J + b.N ne sont pas élément de F car J est maximal, en conséquence ils contiennent des produits d'idéaux premiers :

$\mathfrak J + aN \supset \mathfrak P_{a1}\mathfrak P_{a2}\cdots \mathfrak P_{ap_a}\quad \text{et}\quad \mathfrak J + bN \supset \mathfrak P_{b1}\mathfrak P_{b2}\cdots \mathfrak P_{bp_b}$

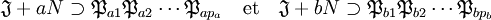
Les inclusions suivantes fournissent la contradiction recherchée :

$\mathfrak J \supset (\mathfrak J + aN)(\mathfrak J + bN) = \mathfrak J^2 + a\mathfrak J + b\mathfrak J + abN\supset \mathfrak P_{a1}\mathfrak P_{a2}\cdots \mathfrak P_{ap_a} \mathfrak P_{b1}\mathfrak P_{b2}\cdots \mathfrak P_{bp_b}$

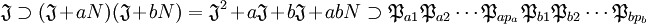
Ce qui termine la démonstration.

• Le module M est noethérien si et seulement si P et M / P le sont aussi :

Supposons dans un premier temps que M soit noethérien. Tout sous module de M et donc a fortiori de P sont de type fini, ce qui montre que P est noethérien. Soit Q un sous-module du quotient M / P, l'image réciproque de Q par la projection canonique de M dans M / P est un sous-module et contient une famille génératrice finie. L'image par la projection canonique de cette famille est génératrice de Q, ce qui montre que le quotient est aussi noethérien.

Réciproquement supposons que P et M / P soient noethériens. Soit (S_n) une suite croissante de sous-modules de M . L'objectif est de montrer qu'à partir d'un certain rang, cette suite est stationnaire. Soit K_n l'intersection de S_n avec P et C_n la projection canonique de K_n dans M / P. Les deux suites K_n et C_n sont croissantes dans des modules noethériens, elles sont donc stationnaires au bout d'un certain rang.

Soit ν un entier tel que les suites K_n et C_n sont constantes après ν. Montrons que si n est plus grand que ν, S_n est égal à S_ν. Soit s_n un élément de S_n, comme C_n et C_ν sont égaux, il existe un élément s_ν de S_ν et un élément k_ν de K_ν tel que :

$s_n = s_{\nu} + k_{\nu}\;$

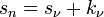
Or s_ν et k_ν sont élément de S_ν, ce qui montre que s_n est élément de S_ν et donc que la suite est constante à partir d'un certain rang.

• Le module à gauche N ⁿ est noethérien :

Démontrons cette propriété par récurrence. Si n égal 1, par hypothèse N est noethérien, donc N¹ est aussi noethérien.

Supposons la propriété démontrée pour n - 1 et montrons là pour n. La projection canonique de N ⁿ dans N ^n-1 qui à (a₁, ... , a_n-1, a_n) associe (a₁, ... , a_n-1) possède pour image N ^n-1 et pour noyau l'ensemble K des n-uplets de la forme (0,...,0,a_n). Le noyau K est isomorphe à N, il est noethérien par hypothèse. L'image est noethérienne par hypothèse de récurrence. La proposition précédente permet de conclure.

 

Exemples

Premiers cas

Tout corps est manifestement noethérien, par absence d'idéaux non triviaux. Tout anneau principal est aussi noethérien car chaque idéal est engendré par un unique élément, ainsi Z, K[X] l'anneau des polynômes à coefficients dans un corps est noethérien. En revanche, lorsque c'est possible, il est plus simple de les étudier à l'aide d'une division euclidienne ou, ce qui est toujours possible, d'utiliser le théorème fondamental de l'arithmétique dans le cadre d'un anneau factoriel.

Tout anneau fini est noethérien, on trouve leur présence, par exemple dans le cadre de la géométrie algébrique ou de la théorie algébrique des nombres.

Polynômes

Un anneau de polynômes n'est pas toujours principal, Z[X] est un exemple déjà cité. Un anneau de polynôme en plusieurs indéterminées Q[X, Y] n'est pas non plus principal, l'idéal des polynômes de degré supérieurs ou égal à 1 nécessite deux générateurs, les indéterminées X et Y.

Le théorème suivant, découvert par David Hilbert en 1888^[4] et parfois nommé Théorème de la base de Hilbert établit que les anneaux de polynômes à une indéterminée noethériens sont nombreux :

• Soit A un anneau commutatif noethérien, l'anneau des polynômes A[X] est noethérien.

Un corollaire permet de considérer le cas de plusieurs indéterminées :

• Soit A un anneau commutatif noethérien et n un entier strictement positif, l'anneau des polynômes A[X₁, ...,X_n] est noethérien.^[5]

En revanche, l'anneau des polynômes d'un nombre infini d'indéterminées ne l'est pas. Il suffit de considérer la suite d'idéaux dont le n^ième est engendré par (X₁, ...,X_n) pour obtenir une suite qui n'est pas stationnaire à partir d'un certain rang.

Comme exemple d'utilisation, on peut imaginer en géométrie une surface algébrique S définie comme l'ensemble des racines d'une famille infinie de polynômes à plusieurs indéterminées et sur un anneau noethérien. Le théorème de la base de Hilbert indique qu'il suffit de considérer une famille finie de polynômes pour définir S. En effet, l'ensemble des polynômes s'annulant sur S forme un idéal.

Démonstrations

• L'anneau des polynômes A [X] est noethérien :

Soit J un idéal de A[X]. l'objectif est de montrer que J est de type fini. Si tel est le cas, tout idéal de A[X] de type fini, alors l'anneau est noethérien.

Soit (D_n) la suite d'idéaux de A définie par:

$D_n=\{o\} \cup \{a \in \mathbb A /\ \exists P[X] \in \mathfrak J,\; \exists (a_i) \in \mathbb A^{n-1} \ \text{avec} \ P[X]= a X^n + \sum_{i=0}^{n-1} a_i X^i \}$

On remarque que si a est un élément de D_n, alors a est le coefficient du monôme dominant d'un polynôme P[X] de degré n de J et a est aussi le monôme dominant du polynôme X.P[X] et est donc élément de D_{n + 1}. Ceci démontre que (D_n) est une suite croissante d'idéaux, et comme A est noethérien, elle est stationnaire à partir d'un rang r. La réunion de tous les D_n est un idéal de type fini égal à D_r.

Chaque D_n est un idéal de type fini car A est noethérien, soit (a_ni) une famille génératrice de D_n et P[X]_ni un polynôme de J de degré n et de coefficient du monôme dominant égal à a_ni, qui existe par définition de D_n.

Montrons que (P[X]_ni), pour n inférieur ou égal à r, forme un système générateur de J. Cette assertion indique que tout polynôme Q[X] s'exprime comme combinaison linéaire à coefficients dans A de la famille (P[X]_ni). On procède par récurrence sur le degré d de Q[X].

Si d est égal à 0, on remarque que D₀ est l'idéal de A correspondant aux polynômes constant de J. La famille (a_0i) est génératrice de cet idéal, et donc la famille (P[X]_ni) engendre bien les polynômes constants de J.

• Supposons que le système soit générateur pour tout polynôme de degré inférieur à d - 1.

Soit Q[X] un polynôme de degré égal à d. Soit q_{d + 1} le coefficient de son monôme dominant. Par construction de (a_ni), q_{d + 1} est combinaison linéaire de la famille (a_ri) si d est strictement plus grand que r et de la famille (a_di) sinon. Il existe en conséquence, une famille (μ_di) d'éléments de A tel que :

$q_d=\sum_i \mu_i a_{di} \quad \text{et}\quad \deg \; \Big(Q[X] - \sum_i \mu_i P_{di}[X]\Big)\le d-1$

L'hypothèse de récurrence montre que Q[X] est engendré par la famille (P[X]_ni).

On a montré que J est un idéal de type fini, tout idéal de A[X] est de type fini, ce qui montre que l'anneau des polynômes est bien noethérien.

• L'anneau des polynômes A [X₁, ...,X_n] est noethérien :

Un raisonnement par récurrence, permet de démontrer la proposition. Si n est égal à 1, alors la proposition précédente permet de conclure. Supposons le résultat vrai à l'ordre n - 1 et soit B l'anneau A [X₁, ...,X_n-1]. L'anneau B est noethérien par hypothèse de récurrence, et la proposition précédente montre que B [X] est aussi noethérien. Or B [X] est isomorphe à A [X₁, ...,X_n] (cf polynôme en plusieurs indéterminées), ce qui termine la démonstration.

 

Anneau d'entiers algébriques

Plusieurs exemples d'anneaux noethérien proviennent de l'arithmétique. L'origine de ses anneaux provient de l'étude d'équations diophantiennes, même si leur utilisation dépasse maintenant largement ce cadre. Un exemple simple est donné par le théorème des deux carrés de Fermat, l'anneau des entiers Z est enrichi par celui des entiers de Gauss. Une approche simple est celle des entiers quadratiques. Cette famille d'anneaux, dit de anneau de Dedekind sont tous noethériens.

Le contexte général est celui d'un anneau A ici commutatif unitaire intègre et noethérien. Soit K son corps des fractions et L une extension finie de K, que l'on suppose séparable. L'ensemble considéré B est celui des entiers algébriques de L sur A, c'est-à-dire l'ensemble des éléments de L dont le polynôme minimal est à coefficients dans A. L'article Polynôme minimal d'un nombre algébrique montre que B est un anneau contenant A. Il est clairement commutatif unitaire et intègre, il dispose de plus de la propriété suivante :

• L'ensemble B est noethérien, à la fois vu comme un A module et comme un anneau.

Ce résultat est lourd de conséquences, par exemple en théorie algébrique des nombres. La démonstration proposée ici utilise un outil, appelé forme trace utilisé aussi pour définir le discriminant d'un anneau d'entiers algébriques.^[6] Une démonstration plus simple est proposée dans le cas particulier des entiers quadratiques dans l'article Idéal de l'anneau des entiers d'un corps quadratique.

Un autre anneau possède d'importantes propriétés noethériennes, il correspond au localisé d'un anneau noethérien N. Si P est un idéal premier de N un anneau commutatif unitaire intègre noethérien et intégralement clôt (de corps des fractions encore noté K), le localisé de N en P, souvent noté N_(P) est l'anneau des fractions de type u/v avec u élément de N et v élément de N - P.

• L'anneau N_(P) est noethérien, à valuation discrète.

Démonstrations

• L'ensemble B est noethérien, à la fois vu comme un A module et comme un anneau :

Si le A module B est noethérien, c'est-à-dire si tous les sous-modules sont des ensembles de combinaisons linéaires à coefficients dans A d'une famille finie, à fortiori tout idéal, qui est aussi un sous-module, est composé combinaisons linéaires à coefficients dans l'ensemble B contenant A, d'une famille finie. Ce qui signifie que si B est noethérien comme A module, il l'est comme anneau.

L'objectif est de montrer que B est isomorphe à un sous-module d'un A module noethérien. Dans un premier temps, remarquons que B contient un sous-module libre de type fini. Le corps L est une extension finie séparable de K par hypothèse. Le théorème de l'élément primitif montre l'existence d'un élément x de L tel que K[x] est égal à L. En multipliant le polynôme minimal de x par le produit a_n des dénominateurs de ses coefficients, on obtient une relation de la forme suivante définissant un polynôme P[X] unitaire à coefficients dans A et irréductible :

$\exists a_i \in \mathbb A, \quad P[a_nx] = (a_nx)^n + a_{n-1}(a_nx)^{n-1} + \cdots + a_1a_{n-1}^{n-2}(a_nx) + a_0a_{n-1}^{n-1} = 0$

On en déduit que a_nx est un entier algébrique et que le sous-anneau A[a_nk] de B est un A-module libre de type fini, notons n sa dimension. Soit <.,.>_L/K la forme trace de L sur K, c'est-à-dire la forme bilinéaire définie sur le K espace vectoriel L, qui à a et b associe la trace de l'endomorphisme φ_ab défini par :

$\forall t \in \mathbb L ,\quad \varphi_{ab}(t) = abt \;$

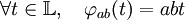
L'extension est séparable, la forme trace est en conséquence non dégénérée (cette propriété est démontrée dans l'article Forme trace). Considérons la restriction de <.,.>_L/K à B x A[a_nx], c'est aussi une forme bilinéaire non dégénérée. Elle induit un morphisme ψ de A module de B dans l'ensemble des formes linéaires du A module A[a_nk]. Le morphisme est défini par :

$\forall h \in \mathbb B,\; \forall a \in \mathbb A[a_n.x] \quad \psi_h(a) = \langle h,h \rangle_{\mathbb L/\mathbb K}$

On en déduit que B est isomorphe à un sous-module du module dual d'un module libre de type fini. Or le dual d'un module libre de type fini est aussi un module libre de type fini, donc isomorphe à Aⁿ. Une proposition précédente montre qu'un tel module est noethérien et en conséquence tous ses sous module. On en déduit que B est isomorphe à un A module noethérien et est donc noethérien.

• L'anneau N_(P) est noethérien, à valuation discrète.

Soit J un idéal de N_(P), remarquons que l'inclusion suivante est vérifiée :

$(1)\quad \mathfrak J = (\mathfrak J \cap N)N_{(\mathfrak P)}$

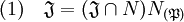
En effet, J est un idéal, donc le produit de tout élément de J par un élément de N_(P) est encore un élément de J et l'ensemble de gauche de l'égalité contient l'ensemble de droite. Réciproquement, soit u / v un élément de J, v est un élément de N qui n'est pas élément de P, c'est donc un élément inversible de N. On remarque que u = (u / v) v est un le produit d'un élément de J et d'un élément de N_(P), c'est donc un élément de l'intersection de J et de N_(P). L'élément 1 / v est dans N_(P), ce qui démontre l'inclusion réciproque.

Soit (J_n) une suite croissante d'idéaux de N_(P), soit (L_n) la suite des intersections de J_n avec N, elle est stationnaire car N est noethérien. L'égalité (1) montre que la suite (J_n) est stationnaire à partir d'un certain rang et donc que N_(P) est noethérien.

L'anneau N_(P) est noethérien, intégralement clôt et ne contient qu'un unique idéal premier. Ces propriétés caractérisent un anneau à valuation discrète. Une démonstration de cette propriété est proposée dans l'article Anneau à valuation discrète.

 

Notes et références

Notes

1. ↑ M. Yoshida M. Sakuma On integrally closed noetherian rings J. of Sc. of Hiroshima Univ Series A tome 17 1954 p. 311-315
2. ↑ On trouve une démonstration analogue p 22 dans le site : Théorie algébrique des nombres un cours de maîtrise par Bas Edixhoven de l'Université de Renne I.
3. ↑ Ces démonstrations sont disponibles p 110 sur le site Algèbre commutative par A. Chambert-Loir Cours à l’Université de Rennes 1 (2006–2007)
4. ↑ La preuve de Hilbert provoqua une vaste polémique à son époque. La preuve n'est en effet pas constructive, elle démontre l'existence d'une base sans indiquer comment l'obtenir. Gordan, le spécialiste de la question s'exclama Ce n'est pas des mathématiques, c'est de la théologie, il finit quelques années plus tard par admettre cette preuve et indiqua que J'ai acquis la conviction que la théologie a aussi ses avantages : J. Boniface Hilbert et la notion d'existence en mathématiques Librairie Philosophique Vrin 2004 Chap 2 p 53 et Chap 1 p 15 (ISBN 2711616061)
5. ↑ Deux démonstrations analogues se trouve p 122 sur le site Algèbre commutative par A. Chambert-Loir Cours à l’Université de Rennes 1 (2006–2007)
6. ↑ Une démonstration est donné p III 3 sur le site Nombres algébriques et nombres p-adiques par Loïc Merel cours préparatoire aux études doctorales 2003-04

Liens externes

• (fr) Algèbre commutative par A. Chambert-Loir Cours à l’Université de Rennes 1 (2006–2007)
• (fr) Nombres algébriques et nombres p-adiques par Loïc Merel cours préparatoire aux études doctorales 2003-04

Références

• (fr) Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
• (fr) N. Bourbaki Eléments de mathématique. Algèbre commutative. Chapitre 8: Dimension. Chapitre 9: Anneaux locaux noethériens complets Hermann 1983 (ISBN 2225787166)
• (en) Cox, Little, and O'Shea, Ideals, Varieties, and Algorithms 2^nd éd Springer-Verlag, 1997 (ISBN 0387946802)
• (fr) Pierre Samuel, Théorie algébrique des nombres [détail des éditions]

Ce document provient de « Anneau noeth%C3%A9rien ».