- Anneau integre
-
Anneau intègre
Un anneau intègre ou anneau d'intégrité[1] est, en mathématiques et plus particulièrement dans la théorie des anneaux, un anneau (unitaire) qui ne possède aucun diviseur de zéro, et non réduit à l'élément neutre pour la première loi.
Sommaire
Définition
Un anneau
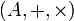 est dit intègre, s'il est non réduit à l'élément neutre de la première loi et ne possède aucun diviseur de zéro, c’est-à-dire que tout élément non nul de A est régulier pour la deuxième loi notée multiplicativement, soit encore :
est dit intègre, s'il est non réduit à l'élément neutre de la première loi et ne possède aucun diviseur de zéro, c’est-à-dire que tout élément non nul de A est régulier pour la deuxième loi notée multiplicativement, soit encore :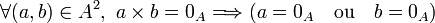
Par convention, l'anneau nul {0A} n'est pas intègre.
En pratique, travailler dans un anneau intègre permet de résoudre des équations produit-nul.
Si un anneau A est intègre, l'ensemble A-{0} des éléments non nuls forme une partie multiplicative de A, c'est-à-dire stable par la multiplication de A. Cette propriété permet de définir le procédé de localisation sur un anneau. Si l'anneau A est unitaire, A-{0} est un monoïde.
Nicolas Bourbaki[2] et de nombreux auteurs imposent dans leur définition à un anneau intègre d'être commutatif, mais ne l'imposent pas pour la définition d'un corps, cela est justifié par les propriétés qu'ont les anneaux intègres commutatifs.
Propriétés des anneaux commutatifs intègres
- Par le procédé de localisation, tout anneau (commutatif) intègre peut être plongé dans un corps. Il existe à isomorphisme près un plus petit corps dans lequel il peut être plongé, appelé le corps des fractions.
Article détaillé : Corps des fractions.- Un anneau (commutatif) A est intègre si et seulement si son anneau des polynômes A[X] l'est.
- Un anneau I intègre commutatif et fini est un corps (
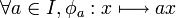 de I dans lui même est bijectif car injectif à cause de l'intégrité, d'où l'existence de y tel que φa(y) = 1).
de I dans lui même est bijectif car injectif à cause de l'intégrité, d'où l'existence de y tel que φa(y) = 1).
Exemples
- Tout corps est un anneau intègre (non nécessairement commutatif).
- L'ensemble
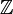 des entiers relatifs est un anneau intègre. Par définition,
des entiers relatifs est un anneau intègre. Par définition, 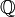 est son corps des fractions.
est son corps des fractions. - L'anneau des congruences modulo 6 noté
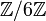 n'est pas intègre car on peut y écrire
n'est pas intègre car on peut y écrire 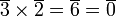 . Plus généralement l'anneau des congruences modulo n noté
. Plus généralement l'anneau des congruences modulo n noté 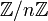 est intègre si et seulement si n est premier, et dans ce cas, c'est un corps, ou si n est nul.
est intègre si et seulement si n est premier, et dans ce cas, c'est un corps, ou si n est nul. - Si un anneau A est commutatif et si I est un idéal propre de A, l'anneau A/I est intègre si et seulement si l'idéal I est un idéal premier.
- L'anneau
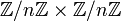 n'est pas intègre, (1,0) et (0,1) sont deux éléments non nuls dont le produit est nul. Plus généralement, le produit de deux anneaux (unitaires non nuls) n'est pas intègre.
n'est pas intègre, (1,0) et (0,1) sont deux éléments non nuls dont le produit est nul. Plus généralement, le produit de deux anneaux (unitaires non nuls) n'est pas intègre. - L'anneau des matrices carrées de taille n ≥ 2 à coefficients réels n'est pas intègre (il n'est pas commutatif et il admet des diviseurs de 0 : les matrices de rang strictement inférieur à n, les matrices nilpotentes par exemple).
Notes et références
- Portail des mathématiques
Catégories : Anneau | Zéro
Wikimedia Foundation. 2010.
