Angles correspondants
- Angles correspondants
-
En géométrie, lorsque deux droites sont coupées par une sécante, il se forme des angles dont les sommets sont aux points d'intersection.
Les angles correspondants sont isométriques lorsque les deux droites sont parallèles.
De plus, pour que deux angles soient correspondants, il faut que ceux-ci se situent du même côté de la sécante, alternes ou externes.
Droites quelconques
Il est impossible de déterminer des angles avec seulement des droites quelconques mais possible avec des renseignements extérieurs, par exemple : forme géométrique indiquant un angle, une longueur, un cosinus/sinus/tangente, etc.[réf. souhaitée]
Droites parallèles
Sur la figure suivante, les droites a et b sont parallèles, s est une sécante quelconque.
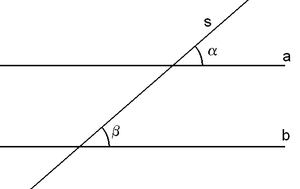 α et β sont des angles correspondants égaux.
α et β sont des angles correspondants égaux.
- Propriété
- Si les droites sont parallèles, alors les correspondants sont égaux.
- Réciproquement, si deux angles correspondants sont égaux, alors les droites sont parallèles.
Voir aussi
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Angles correspondants de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Angles Correspondants — En géométrie, lorsque deux droites sont coupées par une sécante, il se forme des angles dont les sommets sont aux points d intersection. Les angles correspondants sont isométriques lorsque les deux droites sont parallèles. Droites quelconques… … Wikipédia en Français
Angles correspondants — ● Angles correspondants paires de demi droites A x, A y et B x, B z telles que A appartient à [B x) ou B à [A x) et telles que [A y) et [B z) soient incluses dans le même demi plan de frontière (AB) … Encyclopédie Universelle
Angles d'euler — Pour les articles homonymes, voir Euler. Le mouvement d un solide par rapport à un référentiel fait intervenir 6 paramètres, qui sont, par exemple, les trois coordonnées décrivant la position de son centre de masse (ou d un point quelconque du… … Wikipédia en Français
Angles Alterne-interne — Angles alternes internes En géométrie, deux droites coupées par une sécante forment des angles dont les sommets sont aux points d intersection. Sommaire 1 Définition 2 Droites quelconques 3 Droites parallèles … Wikipédia en Français
Angles alterne-interne — Angles alternes internes En géométrie, deux droites coupées par une sécante forment des angles dont les sommets sont aux points d intersection. Sommaire 1 Définition 2 Droites quelconques 3 Droites parallèles … Wikipédia en Français
Angles Alterne-externe — Angles alternes externes En géométrie, lorsque deux droites sont coupées par une sécante, il se forme des angles dont les sommets sont aux points d intersection. Deux angles sont dits angles alternes externes si : ils sont situés de part et… … Wikipédia en Français
Angles alterne-externe — Angles alternes externes En géométrie, lorsque deux droites sont coupées par une sécante, il se forme des angles dont les sommets sont aux points d intersection. Deux angles sont dits angles alternes externes si : ils sont situés de part et… … Wikipédia en Français
Angles adjacents — ● Angles adjacents angles définis par deux couples de demi droites, tels que la deuxième composante d un couple soit la première de l autre, les deux secteurs angulaires correspondants étant situés de part et d autre de cette demi droite … Encyclopédie Universelle
Angles d'Euler — Le mouvement d un solide par rapport à un référentiel fait intervenir 6 paramètres, qui sont, par exemple, les trois coordonnées décrivant la position de son centre de masse (ou d un point quelconque du solide) et trois angles, nommés les angles… … Wikipédia en Français
Angles alternes-internes — En géométrie, deux droites coupées par une sécante forment des angles dont les sommets sont aux points d intersection. Sommaire 1 Définition 2 Droites quelconques 3 Droites parallèles … Wikipédia en Français
 α et β sont des angles correspondants égaux.
α et β sont des angles correspondants égaux.